|
GEOMETRY OF DEMOCRACY TOHRU OGAWA and TAEKO OGAWA
Name: Tohru Ogawa Address: University of Tsukuba;
3-197, Edogawadai-Higashi, Nagareyama
Name: Taeko Ogawa Address: Saitama Junior College; 3-197, Edogawadai-Higashi, Nagareyama Email (for both): ogawa-t@koalanet.ne.jp Phone & fax: +81-471-4714
Abstract:
One-person, one vote is a basic principle of democracy. What is the fairest
allocation system of the seats to parties in election? It is an interesting
mathematical problem. Proportional representation is introduced in many
countries. It is applied for allocation of the seats sometimes to parties
and sometimes to states. There are essentially two allocation schemes of
seats, by D’Hondt and by Sainte Lagües. Here a new interpretation
of these schemes is proposed and geometrically analyzed. How does fairness
look as geometrical feature? What is the shape in Euclidean space? The
main part of the presentation is the geometrical part.
1. Proportional Allocation in Electoral System The problem of allocation in electoral system is to find the proper set of the same number of integers as that of parties; the sum of them is a given number and the ratio of them is as close to the percentage of votes as possible. The scheme by D’Hondt is conventionally explained with its allocation procedure as follows. Suppose there are k
parties (1, 2,…, k), their
number of votes are respectively Vi
(i=1, 2,…, k),
the total number of votes is The conventional explanation of the scheme is based on the practical procedure of the allocation. It is summarized as follows. First, make a table of the number of votes divided by positive integers party by party. Next, make the list of the largest N numbers among the table. Party i get Ni seats if Ni numbers are included in the list of N numbers just mentioned. The hidden principle of the D’Hondt scheme, which the above procedure based on, is to keep the balance in the number of the votes per a seat between the parties. It is formulated in a mathematical expression: the following relation must hold between any two parties i and j.
New interpretation can be simply understood. Some proper number L can be find so that Ni < niL < Ni+1 and Generally, the number L lies in some range. The only exception is accidental degeneracy. For example, any scheme has nothing to do if the number of votes of some different parties is the same and they are at the critical line. It is noted that the expression
in terms of N/V is more easy
to put some meaning than those in terms of V/N
at least in the above mentioned new interpretation and the next example.
The practical procedure in the scheme by Sainte Lagües in similar
to the D’Hondt’s one except that the divisor is restricted to odd numbers
in making table of V/N. Some
textbook describes that the base of the scheme is unclear. But the base
is clear. There are two representative methods in making an integer from
some real number, round down and round off. The former corresponds to the
D’Hondt’s and the latter to the Sainte Lagües’. It is easily seen
in terms of N/V since the
description of rounding off is easier to see.
2. Geometrical Analysis (The case of three parties.) The case of just three parties is a good example since it can be shown in some planer figures. After an election, the initial data is the number or the percentage of the votes to every party. It can be expressed as a point in a regular triangle since the sum of the lengths of three perpendiculars to edge is common to all points in it. An allocation scheme decides a tessellation of the triangle for every given integer so that a polygonal domain corresponds to a set of three integers. The common feature of proportional schemes in this stage is that all the boundary lines of the domains are a part of line radiating out from one of vertices of the triangle. The radiating nature is one of geometrical characteristics of proportionality. It is noted that the case of just two parties appears at an edge here. The radiating nature strictly keeps the allocation to two parties even the third party exists. The three parties in the story up to here can be extended almost in parallel to the case of any three among many. What should be kept in mind is only that the number of available seats for the three depends on the other parts. Such independent natures are also character of proportional allocation. It is noted that all the domains
in Fig. 1 have the same area, irrespective of the shape,
square, pentagon, and hexagon. The areas of the domains in Fig. 2
are three
kinds depending on square, pentagon, or hexagon.
Fig.1. Domains
for 5-seats 3-parties case in D’Hondt
Fig.2. Domains for 5-seats 3-parties case in Sainte Lagüe scheme.
Fig. 3. D’Hondt’s
case. Any vertex of the domains in Fig. 1 is on the line
Fig. 4. Any vertex of the domain in Fig. 2 (Sainte Lagues’ case) is on the line connecting a certain lattice point and the origin in 3D. The lattice points are more distant than D’Hondt’s case in Fig. 3.
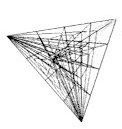
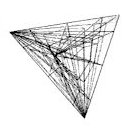
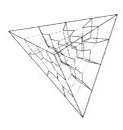
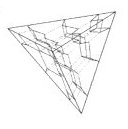
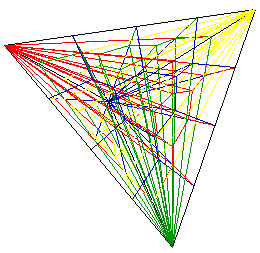
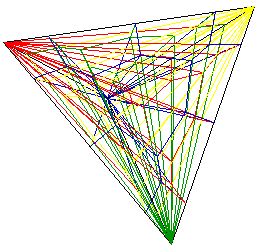
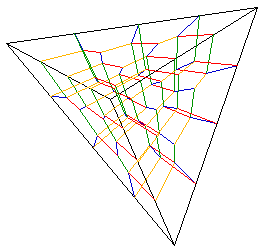
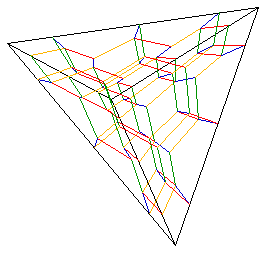
3. General case with more parties The allocation of seats consists
a high dimensional lattice, the dimensionality of which is the number of
the parties. The problem is to find the proper system to find the most
proper lattice point for any distribution of votes. A system divides the
space into domains of lattice points. The borders of such domains direct
to the corner of the space in many respects.
Fig. 5. The case
of four parties shown as tessellation of tetrahedron.
References Tohru Ogawa and Taeko Ogawa; "One-Dimensional
Quasicrystals and Democracy", in Quasicrystals (Eds. K. H. Kuo and
T. Ninomiya, World Scientific, 1991) pp.394-401.
|