Name: Ami Korren, Architect, (b. Tiberias, Israel, 1950).

Address: Faculty of Architecture and Town Planning, Technion, Israel Institute of Technology, Technion City, Haifa 32000, Israel. 

E-mail: Korren-a@inter.net.il

Fields of interest: Architecture; Morphology, geometry, architectural crystallography; and Minimal and consequential forms.

Publication and exhibition: 

Korren, A. (1993) Periodic 2-Manifold Surfaces which Divide the Space into Two Identical Subspaces, [in Hebrew and English], Master Thesis, Haifa: Technion, 120 pp.

Burt, M. and Korren, A. (1995) Self-dual space lattices and periodic hyperbolic surfaces, In: Symmetry: Natural and Artificial, Budapest: Symmetrion, 100-103.

Burt, M. and Korren, A. (1996) Periodic hyperbolic surfaces and subdivision of 3-space, In: Katachi U Symmetry, Tokyo: Springer-Verlag, 179-183.

Korren, A. (1999) [Exhibition], In: Science in the Arts –Art in the Sciences, Budapest: Ernst Museum.
 
 

Abstract: The morphological dealing with space subdivision by continuous 2-manifold surfaces is one of the important issues for understanding organized space and its order. The phenomenon of periodic surfaces that divide the space into two identical subspaces was dealt with over the years by various researchers from different scientific fields. 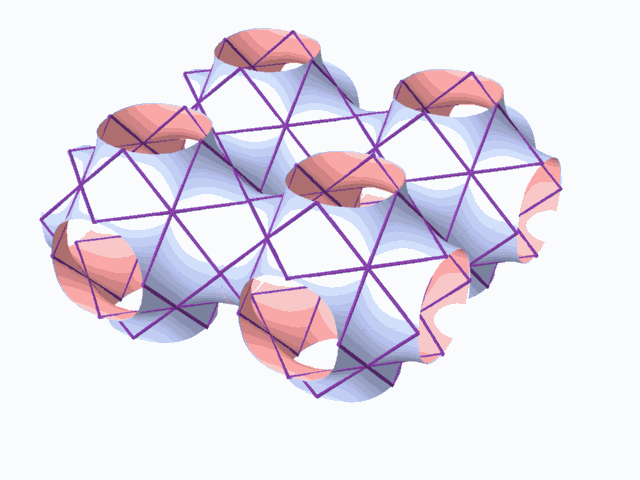These periodic 2-manifold surfaces are continuous and divide the space into two identical subspaces, which are graphically characterized by two dual tunneled space networks. These surfaces have the shape of a sponge structure. All the known surfaces were discovered in an empiric way by various scientific researchers. All in all there were seven topologically different surfaces. The goal of the research of the above mentioned phenomenon was to identify the 2-manifold, classify and exhaust them. A systematic method was suggested. The method was strongly based on the theory of symmetry groups. It was assumed that the number of surfaces, topologically different, is finite because of the fact that the number of symmetry groups is finite. With the method for the exhaustive search the seven known topologically different surfaces were discovered. But now it was done in a systematic way. Topologically different – means that the two dual tunnel networks have different shapes, which are the identification mark of the surface. This identification of the 2-manifolds point out that there is a direct correspondence between the continuous partition surface, the character of the two complimentary subspaces and the two self-dual lattices representing them. This phenomenon of the two identical subspaces, the surface in between, and the two self-dual lattices representing them makes the exhaustive search of any of them as one and the same problem. While studying this phenomenon the idea to search for the self-dual lattice pairs first arose for reasons that will be mentioned later. This approach led the author to discover a new unknown self-dual space network and a new 2-manifold surface in between.
 
 

This paper intends to report on research in which generation of dual space lattices and hyperbolic partition surfaces are at the core of the inquiry. This research is still in its initial stages. This stage, the impression is that the number of the dual and identical lattice pairs and the associated periodic hyperbolic surfaces, partitions that subdivide the entire space into two complementary and identical subspaces, is infinite. 
 

1 The phenomena of 2-manifolds surfaces 
which divide the space into two identical subspaces

The researching of the phenomena of periodic 2-manifolds which are in between two identical - dual subspaces led us to finding the main characteristics of these surfaces.

We have chosen to discuss 2-manifold with 2-fold (180⁰) rotation symmetry axes. These axes generate a space lattice, which should be called "the 2-fold axes lattice". This lattice is periodic, and as such has all the periodicity generating properties, meaning an 3-dimensional repetitive cell unit and elementary periodic region (E.P.R.).
 

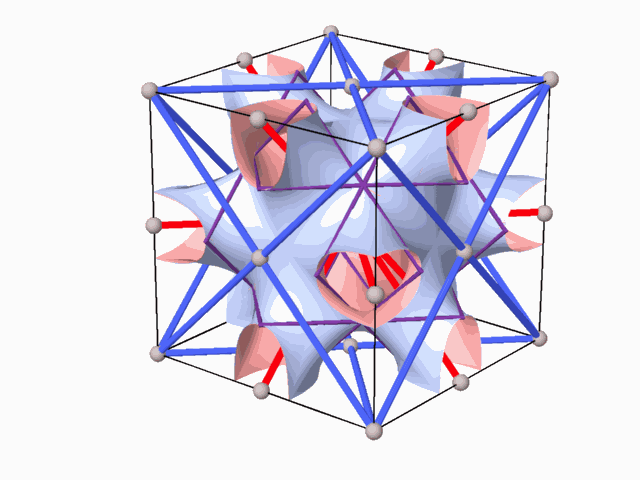
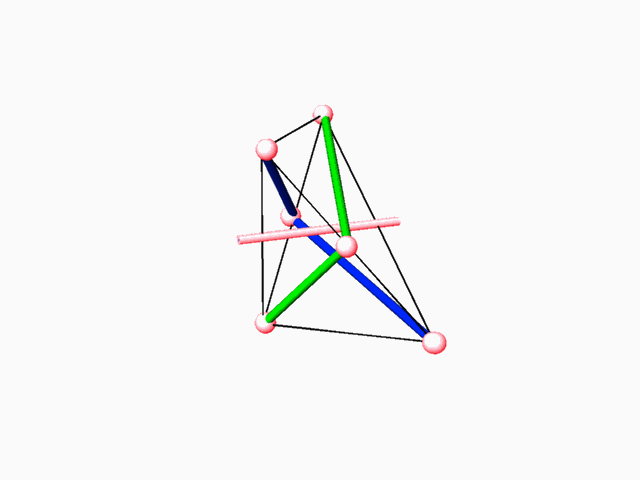
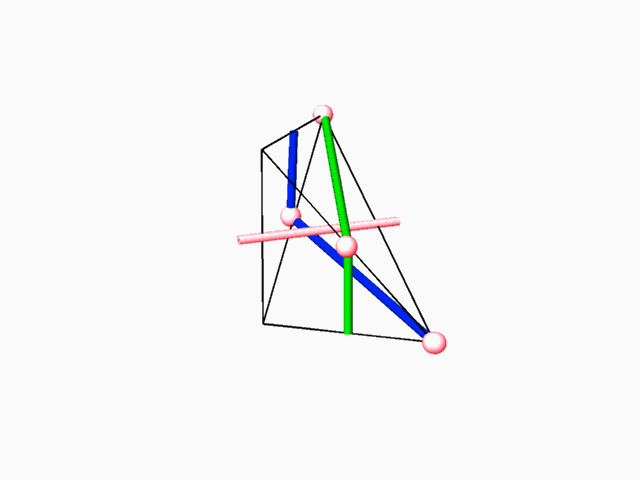
2 The E.P.R. (Elementary Periodic Region) approach

The E.P.R. is the smallest space unit (fundamental region) derived from the Euclidean space by means of the symmetry group that acts on this space.

The E.P.R. contain complete representation of all the phenomena taking place within the "periodic complex" and particularly, representation of the whole periodic space, its symmetry group, the 2-fold axes network, the two complementary (identical) subspaces, the self dual lattices-pair characterizing them, as well as the partion surface in between.
 
 

3 The exhaustive method

The method of exhaustive search develops in steps as follows:

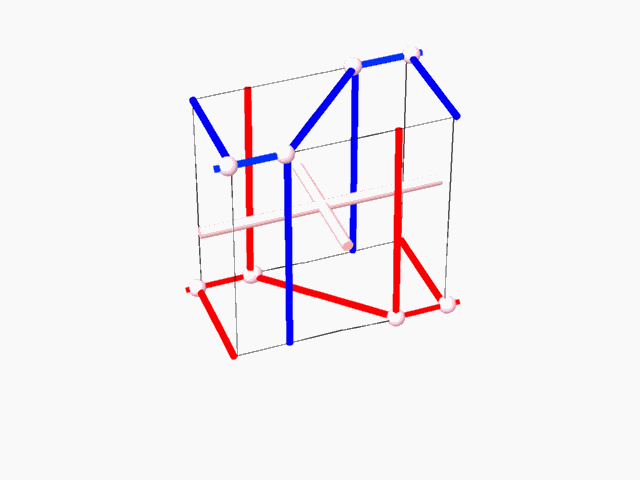
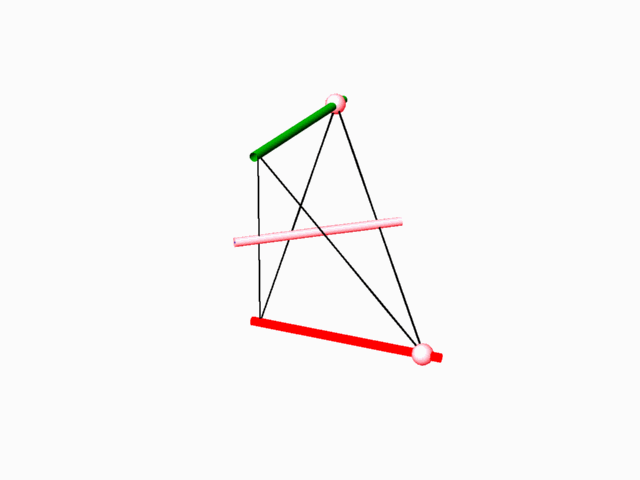
1. Exhaustive search and examination of all the possible E.P.R.s. 

2. Exhaustive search of all possible E.P.R.s capable of containing fundamental region of 2-manifold. Fundamental region of such 2-manifold divides the E.P.R. into two identical volumes and it includes representation of 2-fold axes which transform one subspace into the complementary dual other .

3. Repetitively duplicating the E.P.R. (containing 2-fold axe(s)) until the resulting 2-fold axes lattice is revealed.

4. Identifying, within the 2-fold axes lattice, the possible closed boundary perimeter(s), which could give rise to minimal surface unit (simulating the dipping operation of a wire in sop solution).

5. Duplication of the closed boundary perimeter with the minimal surface unit (through application of the 2-fold axes) to an extent when its general structure, its "tunnel system" and characteristic dual networks could be identified.

4 Classification of the 2-manifolds

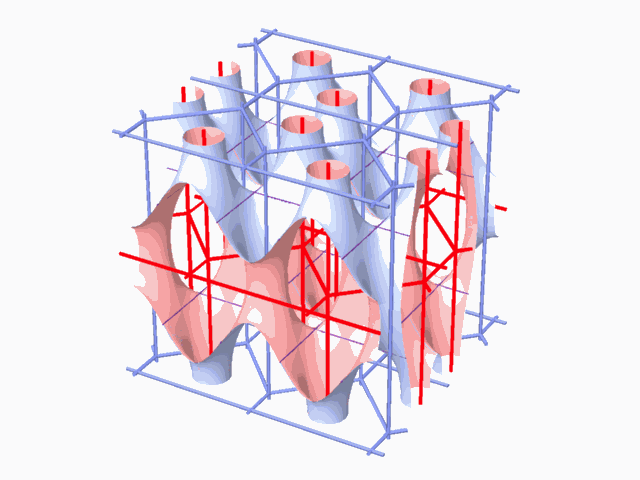
The aforementioned method of searching for the 2-manifolds, lead to the discovery of many 2-manifolds, with some being topologically similar, and it also lead to exhausting all the 2-manifolds that are topologically different.

There are two physical characteristics to the 2-manifolds. One is the form of the translation cell of the 2-manifold. The other one is the geometric form of the two complementary dual subspaces, which are represented by the two dual networks.

There is a direct, one to one correspondence between the typical translation cell and the tunnel networks. 2-manifolds that are characterized by similar tunnel networks are topologically similar.

Classifying the 2-manifolds according to the tunnel networks or the typical translation cell leads to discovering the 2-manifolds that are topologically different from one another. Using the aforementioned searching and classifying method lead to finding seven topologically different 2-manifolds.

The fact that the tunnel networks characterize the 2-manifolds on a direct, one to one correspondence leads to the conclusion that finding two self-dual networks means finding the surface partition in between. Using empiric search for dual networks we have found a new unknown pair of self-dual networks, which are topologically different from the other seven that were found by the aforementioned search method.
 

5 A new search method

Finding the new self-dual network opened the door to revealing a completely new array of surface-partitions and the associated self-dual space networks, which characterize each of the two interwoven, complementary subspaces.

In view of the last development, there is an advantage in shifting the gravity center of the research and pursuing the self-dual lattices pairs first. The new search method is built of several steps, and is partially based on the exhaustive method:

1. Extracting the self-dual lattices directly from the relevant E.P.R.s (containing 2-fold rotation axes) the search of which was exhausted previously.

2. It was done by locating the interconnected configuration of vertices and edges and its rotated image (about the 2-fold axes) within the E.P.R

3. Find the 2-manifold unit, which subdivides between the complementary dual lattices, in a manner that assures continuity and smoothness over the boundaries of the E.P.R. and for the whole periodic hyperbolic surface. It requires that its incidence with the bounding reflection planes will be at right angles all along the incidence curve.

                 

6 Conclusions

In the face of the apparent significance of the subject of dual lattice pairs and the subsequently related continuous Periodic Hyperbolic Surface-partitions, within the general theme of Space Subdivisions, these complementary spatial configurations never occupied a central position in a systematic and exhaustive research inquiry.

It should be noted that these configurations are the abstract idealized prototypes of all sponge structures, all labyrinth-like branching, infinite, enveloped, spaces and other natural phenomena, such as periodic filament configurations and continuous warped fields.

They are an idealized geometric abstraction of continuous labyrinths, which shape the interiors of our modern mega-structures and our evolving urban down town environments.