|
SYMMETRY OF THREE-DIMENSIONAL QUASICRYSTALS Tohru Ogawa Institute of Applied Physics, University
of Tsukuba Sakura, Ibaraki 305, Japan,
The relation between the three-dimensional
quasicrystal models, the one by Penrose transformation method which
was found by the author in 1985 and the other by the so-called projection
method, is clarified. Primitive projection model is formulated as a
mapping from a region in the pseudospace to the physical space by introducing
the concept of the gazing crystal. It makes it possible to study
the structure of the socalled projection method in detail.
In conclusion, the primitive projection model, being deterministic,
is included in the Penrose transformation model in the widest sense,
which, having some freedom, is more flexible to realize some hierarchical
local symmetries.
1. Introduction Penrose tiling [1] is the prototype of the concept of the quasicrystal [2]. However, two-dimensional case, where the Penrose transformation is uniquely defined and coincides with the so-called projection method [3], is rather exceptional when compared with three-dimensional case. Most people seem to believe the Penrose transformation and the projection method (hereafter, to be referred to as the primitive projection) lead always to the same results. In this paper, it is shown to be false and some relations are figured out. It is useful to regard the projection of a regular lattice in a D-dimensional original space to d-dimensional physical space as a mapping from a finite region referred to as the gazing crystal in (D-d)-dimensional pseudo space to ddimensional physical space. Reminisce that some fortune tellers gaze a quartz and decode the information contained in it as that in a whole physical world. From another point of view, there are infinite local five-fold centres in the twodimensional Penrose tiling. Their variety of symmetry range form a kind of hierarchy. On the other hand, the range of icosahedral symmetry in the most strict sense is restricted to the only one case; to be referred to as flower dodecahedron Fl60. Of course, three dimensional configuration can be icosahedrally symmetrical in looser senses, for example in a macroscopic sense that all of the six vectors are evenly appear. In Chapter 2,
three-dimensional Penrose transformation, which was proposed by the author
[4] in 1985, is given in a revised form. In Chapter
3, the primitive projection method is formulated. In Chapter
4, the three-dimensional configuration by the primitive projection
method is studied in detail. Possible symmetry in the projection model
is investigated in Chapter 5. The value t3
of the similarity factor and some similar numbers to golden number are
discussed respectively in Appendix A and B.
The interpretation of three-dimensional Penrose Transformation, which was discovered before by the author [4], is revised below. The quasibases are six vectors arranging
together with their six mirror images with icosahedral symmetry.
where
and
There are 15 = 6C2 rhombi whose edges are these six. They are all congruent as can be seen from the fact that
They are referred to as Golden rhombus
the ratio of whose two diagonals is the golden number
t=(Ö5+1)/2»
1.618. Some properties of a golden rhombus are listed in Table
1. Two kinds of rhombic Penrose tiles in two dimension are the projection
of the rhombus along other quasibases. There are 20 = 6C3
rhombohedra whose edges are these six vectors. They are either of two golden
rhombohedra, acute A6 and obtuse O6. (Tables 2,
3
and 4). They are the quasi-unit-cells of the present
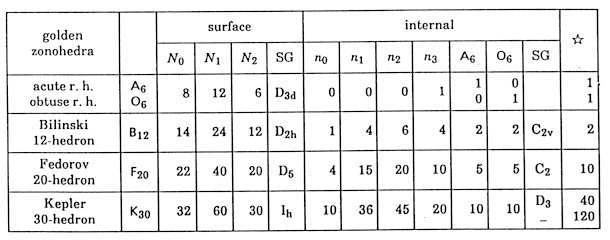
model. Three kinds of zonohedra, B12, F20 and
K30, are constructed with A6 and O6 (Table
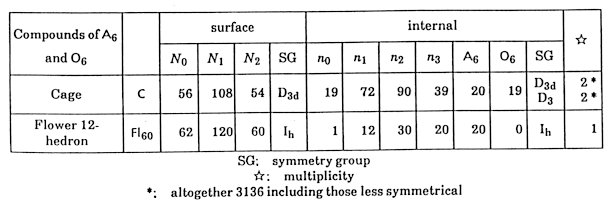
5). Twenty A6's organize a concave 60-hedron Fl60
with icosahedral symmetry so that their principal vertices meet at a point.
In order to give a gross image, this polyhedron is referred to as flower
dodecahedron each of whose 12 faces looks like a five-petalous flower (see
Table
6).
Let us construct an A6* and an O6* (respectively a big A6 and a big O6 of edge length t3) only with A6's and O6's of edge length 1. If it can be done, an A** and an O6** of edge lenght t9 can be constructed in a similar way and so on. Here, a Penrose transformation is defined as a transformation from a set of space-filling figures to their enlarged figures consisting only of the formers. Three-dimensional Penrose Transformation
in the most general version is simply stated as follows:
More exactly, into its centre and of course the Fl60 should be placed so that directions of all edges coincide with the quasilattice axes. It is noted that two Fl60's at both principal vertices of an O6* are connected with each other sharing an A6 in common and six O6's are placed between the two. Though there are many unifilled spaces, in an A6* and an O6*, the skeleton of big rhombohedra have already been essentially decided. The mid part of an edge is almost surrounded with two flowers and can only be filled with a Fedorov icosahedron F20, so long as the tiles are restricted to A6 and O6. The inside of F20 is left undecided in the skeleton structure. Now, the skeleton of an O6* is completely decided. In an A6*, there is a space C, which looks like a cage, can contain 20 A6's and 19 O6's (see Table 6). The shape of the cage is regarded as two Kepler tetrakaidecahedron K30 sharing an O6 in common. The O6 is inevitably placed there, dividing the cage into two parts. Leaving the structure of other parts of the cage undecided, the skeleton of an A6* is thus completely determined. The A6* and O6* are numerically related with A6 and O6 as
A6* = C+20A6 + [6×(1/5)+6×(3/10)] F20
=
55A6 + 34O6 ,
(2.3)
where 20 A6 and 19 A6 correspond to an Fl60 respectively in A6* and O6*. There, the facts
C = 20A6 + 19O6 ,
(2.5)
are also used. The matrix which composed of the coefficients of this equation has t9 and (t-1, t-2) respectively as a set of eigenvalue and eigenvector It means that the limiting tiling obtained by an infinite iteration of this transformation has a self-similarity of factor t3 in linear dimension and t9 in volume and the composition of two tiles are t-1 and t-2. The description should be given on the internal structure of the two undecided parts F20 and C. As F20 has a five-fold axis in its outlook. However, it contains only four points in its inside and it can not have real five-fold symmetry. It can be placed in ten ways for a given axis. There are no principle in this stage to choose some among them. The numbers of A6 and O6 are both five in 10 ways. As mentioned above, a C is a compound of two K30's sharing an O6 in common. A K30, having icosahedral symmetry in its outlook, contains ten points in its inside. Their arrangement is altogether 160 (The value 400 in the previous papers is incorrect). In any of them, a three-fold axis among ten may be regarded as the main axis of the internal structure. On the main axis, an A6 and an O6 are placed so that their principal axes coincide. Now, seven points are already fixed. The part near the A6-side end of the main axis is uniquely filled with three A6's and three O6's. There are eight (=23) possibilities about the position of the remaining three points, each of which has two seats available independently selectable. Six among eight have only reflection symmetry and other two have a three-fold axis. The two correspond to the chirality, which is the symmetry concerning the relation between a left hand and a right hand. Therefore the number of the internal structures is 160 = 23 × 20, by taking the possible choice of the three-fold axis for the main axis into account. The numbers of A6 and O6 are both ten as K30 = 10 A6 + 10 O6 (in 160 ways) (2.8) An O6 is fixed in a cage as a partition and seven O6's are on the surface of a K30. Any of the seven can be chosen as the partition. Therefore the number of the internal structures of a C is 10816 = [23 × (1 + 3 + 32)]2 = 1042 (The value 1642 in the original paper is incorrect), by taking the possible choice of the three-fold axis for the main axis into account. Note that Penrose transformation can be
defined for any choice of these possibilities for F20 and C.
Further more, the highest symmetry is realized by giving three-fold symmetry
to the internal structure of C in A6*. There are four cases
for such configurations, among which two have inversion symmetry at the
centre of C and chirality and other two have reflection symmetry between
two K30's of C. As for the choice for F20's and the
chirality, some aspects from higher point of view is necessary as shown
later in Chapter 5.
|
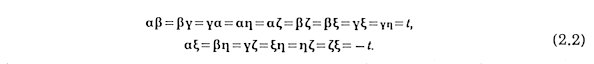
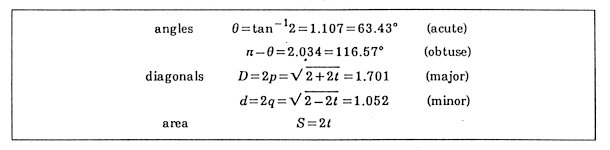


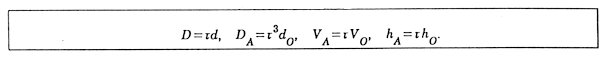
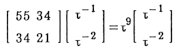 (2.7)
(2.7)