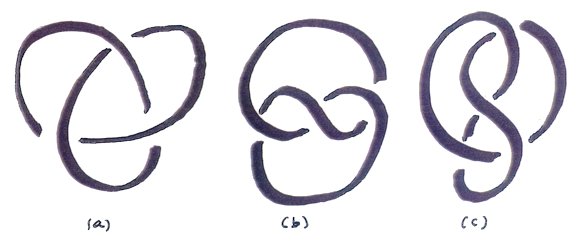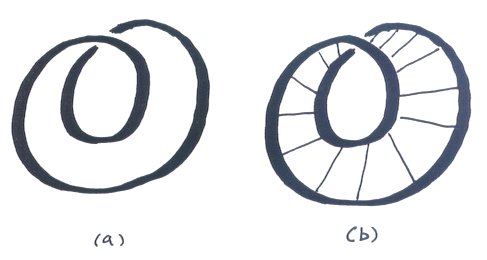Modern computer graphics has emphasized the fact that mathematics is very much a visual subject. Thus the visual mind and visual thinking are of basic importance in mathematics just as in art. Furthermore, visual thinking leads to seeing that mathematical forms can also generate art forms as in the work of the Swiss artist Max Bill. In Figure 1 is shown the granite sculpture Endless Ribbon by Max Bill based on the Möbius band.
 

The Dutch artist Maurice Escher also applied mathematical ideas to generate his art works. Recently the American artist Richard Serra applied the idea of a rotating ellipse as the basis of his now famous Torqued Ellipse sculptures. The Directory at www.isama.org  provides links to a variety of interesting websites relating art, mathematics, architecture, and mathematical visualization. For example, included in the Directory under Sculpture are links to the works of Bruce Beasley, Brent Collins, Helaman Ferguson, Robert Longhurst, Charles Perry, John Robinson, and Keizo Ushio, as well as many others. An excellent general reference on art and mathematics is the book The Visual Mind by Michele Emmer, MIT Press [1].

One can say that the operative word that unifies art and mathematics is SEEING. More precisely, art and mathematics are both about SEEING RELATIONSHIPS. One can see certain mathematical forms as art forms and creativity is about seeing from a new viewpoint. Thus it is all about seeing. As the Basque sculptor Eduardo Chillida states "to look is one thing, to see is another thing", "to look is to try to see", "to see is very difficult, normally" [2]. I would like to add that from my own experience as a research mathematician and sculptor, it can take a lot of looking before one finally sees what has been there all the time. Seeing better is a lifetime endeavor. An excellent related article is See-Duction by Howard Levine [3].

We will now discuss a more complete way of seeing a three-dimensional object that is called hyperseeing. First we note that to see a two-dimensional painting on a wall, we step back from the wall in a third dimension. We then see the shape of the painting (generally rectangular) as well as every point in the painting. Thus we see the painting completely from one viewpoint. Now theoretically, in order to see a three-dimensional object completely from one viewpoint, we would need to step back in a fourth spatial dimension. From one viewpoint, we could then (theoretically) see every point on the object, as well as every point within the object. This type of all-around seeing, as well as a type of x-ray seeing, was known to the Cubist painters such as Braque, Duchamp, and Picasso, as discussed in [4]. In particular, Cubists were led to showing multiple views of an object in the same painting. In mathematics four-dimensional space is referred to as hyperspace and I refer to seeing in hyperspace as hyperseeing ([5]-[8]). Thus in hyperspace one could hypersee a three-dimensional object completely from one viewpoint.
 
 

Cubist painters approximated hyperseeing by showing multiple views in the same painting. Hyperseeing can also be facilitated in our three-dimensional world by viewing a hypersculpture defined as follows. First, a sculpture is defined as an object in a given orientation relative to a fixed horizontal plane (the base). Two sculptures are said to be related if they consist of the same object. Note that related sculptures may look quite different depending on their orientation. A hypersculpture is a set of related sculptures. Thus viewing a hypersculpture allows one to see multiple views of an object from one viewpoint, which therefore helps to develop a type of hyperseeing in our three-dimensional world. Furthermore, a hypersculpture is a more complete presentation of the sculptural content of a three-dimensional form. A first hypersculpture called Rashomon by Charles Ginnever is shown in Figure 2, where three related sculptures are shown. Three other related sculptures are shown below. Actually the form in Rashomon has fifteen stable positions. A second hypersculpture Attitudes by Arthur Silverman is shown in Figure 3. Attitudes consists of six related sculptures. The commen form in Attitudes consists of a rectangle, parallelogram, and two triangles.
 

Figure 2. Rashomon, Charles Ginnever, 1998

Figure 3. Attitudes, Arthur Silverman, 1996
 
 

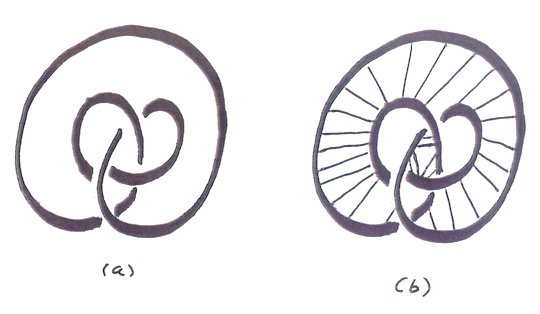
Knots

Knots are usually presented by two-dimensional knot diagrams that indicate where the knot crosses itself. Three diagrams of a trefoil knot are shown in Figure 4.
 

Knots are usually presented as two-dimensional knot diagrams. However, a knot is actually a three-dimensional object and a knot really comes alive in a three-dimensional model of the knot which can be constructed from wire, folded aluminum foil, folded aluminum foil with a wire insert, copper tubing, or other material. Models of knots are ideal mathematical forms that can generate ideas for sculptures. Examples of models of knots made from folded aluminum foil are shown in Figure 5. A knot made from copper tubing is shown in Figure 6.
 

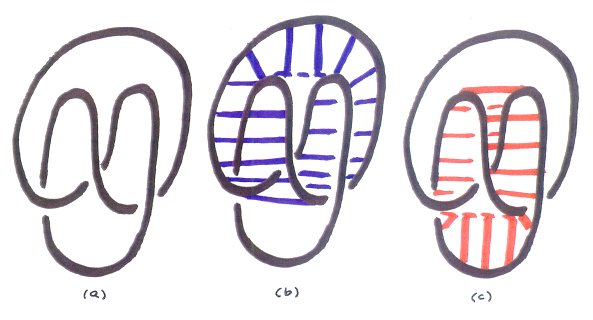
Models of knots are perfect mathematical forms for generating ideas for sculptures. They are completely three-dimensional with no preferred top, bottom, front, or back. Furthermore, a knot can look completely different when viewed from different directions.

In general, we can regard hyperseeing in our three-dimensional world as a more complete all-around seeing from multiple viewpoints. Since knots can look so different from different viewpoints, knots are excellent examples of interesting forms on which to practice hyperseeing. Knots are also open forms that one can actually see through. This is another reason that knots are ideal forms for hyperseeing.

For example, if one makes a wire model of a trefoil knot with front view as in Figure4(a), then the top view will appear similar to Figure 4(b). A right side view of the model with a little tip forward will appear similar to Figure 4(c). In general, a model of a knot yields an infinite number of diagrams of the knot depending on your viewpoint of the knot.

An interesting property that results from the open structure of a knot concerns looking at a model of a knot from opposite directions. Suppose we regard one viewpoint as the front viewpoint. The viewpoint directly opposite will be the rear view. In general, the rear view of an object cannot be determined at all from the front view. However, for a knot, the rear view will be the reflection of the front view with the crossings reversed.. For example, if one considers the views in Figure 4 as front views, then the corresponding rear views can be obtained by holding the turned page to the light and reversing the crossings.

Another property of knots is that one sees all points on a knot in any one view except for a finite number of crossing points. This implies that front and top views determine the side views. To see why this is true, let us fix one point P on the knot in an x,y,z coordinate system. A view along the x-axis determines the y and z coordinates of P. A view along the y-axis determines the x and z coordinates of P. Thus two orthogonal views determine the x,y,z coordinates of P in space. Thus two orthogonal views of a knot will determine the position of the knot in space. In particular, the front and top views determine the side view. This is an interesting exercise in hyperseeing the knot. A suggested first exercise is to consider a straight line in space with endpoints P = (a,b,c) and Q= (d,e,f). A view along the x-axis shows P at (b,c) and Q at (e,f) and a view along the z-axis shows P at (a,b) and Q at (d,e). The view along the y-axis is therefore determined with P at (a,c) and Q at (d,f). One can now connect (a,c) and (d,f) by a straight line to obtain the side view of the line. The next exercise is to consider a knot formed by straight line segments. One can then obtain the side view from front and top views using coordinates of the endpoints of the lines. No line should be parallel to an x,y, or z axis.
 
 

If one dips a wire model of a knot in a solution of liquid soap and water, one obtains a soapfilm minimal surface with the knot as the single edge of the surface. For example, the edge of a half-twist Möbius band is a simple loop as shown in Figure 7(a). If a wire is bent in this shape and dipped in a soap solution, one obtains a minimal surface with a central disk. If this disk is puntured, then one obtains the Möbius band minimal surface in Figure 7(b).
 

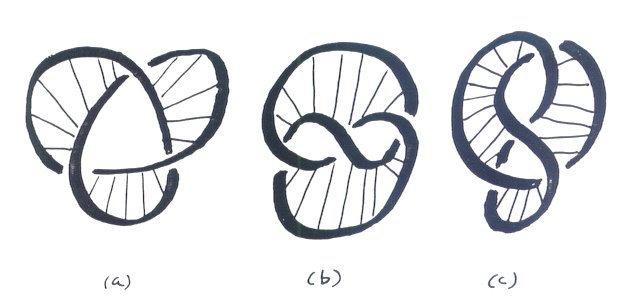
The corresponding soapfilm minimal surfaces for the trefoil knots in Figure 4 are shown in Figure 8. In (a) we have a triple twist Möbius band with one side. In (b) we have a two-sided minimal surface. In (c) we have a one-sided surface.
 

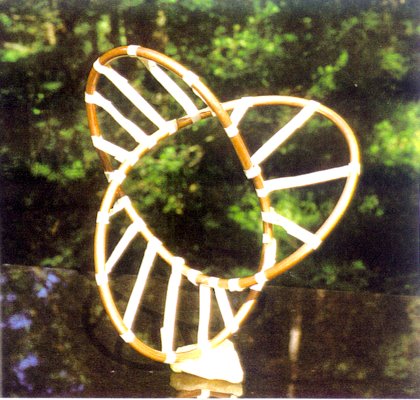
The exercise students of all ages really enjoy is dipping wire models of knots in order to obtain the corresponding soapfilm minimal surfaces. In order that students can learn to anticipate the shape of the surface, it is helpful to use masking tape in order to approximate the surface. An example is shown in Figure 9 for a trefoil knot.
 

In Figure 8(c) we have a minimal surface that could be described as a form consisting of three leaves with a central space. We will now modify the knot so that the leaves become space and the center is form. The modified knot is shown in Figure 10(a) and the corresponding minimal surface is shown in (b). We refer to the knot in (a) as a framed knot. The original idea is to form a link obtained by placing the knot inside a circle. This was first shown to me by the sculptor Charles Perry. Later I saw this link in several books on knots. This led me to the idea of a framed knot. From a mathematical point of view the framed knot is not much different from the original knot since it is easy to see that one can deform the framed knot by lowering the added "frame" to obtain the original knot. However, from a sculptural viewpoint, the framed knot is interesting since it has a minimal surface that reverses form and space in the minimal surface of the original knot. One can also suspend a wire knot in a wire circle using an extra piece of wire to suspend the knot. This is the form that Charles Perry introduced in order to obtain a sculpture where form and space are switched. Perry forms the surface using flexible metal screen and then applies automobile body putty on the screen. A mold is made and then the minimal surface is cast in bronze. The idea of forming a sculpture from the minimal surface of a framed knot or a knot in a circle is a very recent development.
 

In Figure 7(b) we have a minimal surface for a loop that consists of one Möbius band. It will now be shown that there is a configuration of a trefoil knot that has a minimal surface consisting of two Möbius bands that share part of their edges as in Figure 11(a) and also alternately cross over each other as in Figure 11(b). The knot is shown in Figure 12(a). In Figure 12(b) Möbius band 1 is shown and in Figure 12(c) Möbius band 2 is shown. The intersection lines on the crossovers are indicated by dotted lines.
 

If Figures 12 (b) and (c) are combined, then we obtain the complete minimal surface shown in Figure 13. The two bands share parts of their edges and alternately cross over each other. Band 1 crosses over band 2 at the top and band 2 crosses over band 1 at the bottom. It is interesting to see each soapfilm Möbius band twist as it crosses over the other Möbius band. The bands share edges until they twist.
 

The knot in Figures 12 and 13 is the representation of a trefoil knot as the 2-3 torus knot.

In general, given p and q mutually prime, the p-q torus knot wraps meridionally around the torus p times and wraps longitudinally around the torus q times. The p-q torus knot is equivalent to the q-p torus knot. That is, one is deformable into the other ( see [A], page 111 ). Thus from a mathematical viewpoint, the p-q and q-p torus knots are the same knot. However, from a sculptural viewpoint, they look quite different and they have configurations with very different minimal surfaces. In particular, the 3-2 torus knot is shown in Figure 4(a) and it has a minimal surface as in Figure 8(a), which is a triple twist Möbius band. In Figure 13 we have the 2-3 torus knot with a configuration having a minimal surface consisting of two single twist Möbius bands.

In general, the n-(n+1) torus knot has a configuration with a minimal surface consisting of n single twist Möbius bands that partly share edges and alternately cross over each other.

For example, the 3-4 torus knot has a minimal surface consisting of three single twist Möbius bands. Suppose we color these three bands red, white, and blue. Part of the surface will have the red band and white band sharing an edge with the red band to the left of the white band. The blue band will be crossing over the red and white bands. The blue band will then twist and share an edge with the white band, where the white band is now to the left of the blue band. The red band will now twist and cross over the white and blue bands. This structure goes around a central space so that each band twists once to cross the other two bands. In order to picture this, we will first draw the 3-4 torus knot as in Figure 14. We begin with three points as in (a). We then draw arcs as in (b). The knot is completed as in (c). The corresponding minimal surface is shown in Figure 15.
 

Models of the multiple Möbius band minimal surfaces in Figures 13 and 15 are shown in the paper Knots and Multiple Möbius Bands published in Visual Mathematics.

The behavior of minimal surfaces for configurations of (n+1)-n torus knots may consist of one or more bands with one or more half twists. In Figure 8(a) for the 3-2 torus knot we have one band with three half twists. The 4-3 torus knot has a minimal surface consisting of two bands that partly share edges and cross over each other twice, hence each band has two half twists. The 5-4 torus knot has a minimal surface that consists of one band that crosses itself five times as it wraps around four times. Part of the surface will appear as described above for the 3-4 torus knot except there is only one band alternately crossing over itself as it wraps around.

[1] M. Emmer, The Visual Mind, MIT Press, (1993).

[2] E. Chillida, Basque Sculptor, Video, Home Vision, 24, (1985).

[3] H. Levine, See-Duction, Humanistic Mathematics Network Journal #15, (1997).

[4] L.D. Henderson, The Fourth Dimension and Non-Euclidean Geometry in Modern Art, Princeton University Press, (1983).

[5] N.A. Friedman, Hyperspace, Hyperseeing, Hypersculptures, Conference Proceedings, Mathematics and Design 98, Javier Barrallo, Editor, San Sebastian, Spain.

[6] N.A. Friedman, Hyperseeing, Hypersculptures, and Space Curves, Conference Proceedings, 1998 Bridges: Mathematical Connections in Art, Music, and Science, Reza Sarhangi, Editor, Winfield, Kansas, USA. (also published in Visual Mathematics)

[7] N.A. Friedman, Hyperspace, Hyperseeing, Hypersculptures (with figures), Hyperspace, volume 7, 1998, Japan Institute of Hyperspace Science, Kyoto, Japan.

[8] N.A. Friedman, Geometric Sculptures for K-12: Geos, Hyperseeing, Hypersculptures, Conference Proceedings, 1999 Bridges: Mathematical Connections in Art, Music, and Science, Reza Sarhangi, Editor, Winfield, Kansas, USA.