

: Mathematica Programs
: Curious Properties of Reiterated
: Loops of the Digit
In this section we are going to study another process that has been proposed by the authors.
We define the dfsf function by
.gif) , where
, where
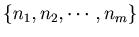 is the list of the digits of an integer n . we start with any positive
integer n, and repeatedly apply the function dsf, then we can generate
a sequence of integers
is the list of the digits of an integer n . we start with any positive
integer n, and repeatedly apply the function dsf, then we can generate
a sequence of integers  suuretu.gif) .
.
Example 9.1.
If we apply dfsf function to the number 228702286, then in 13 steps the sequence enters into a loop of three numbers. See Graph 9.1.
If we apply dfsf function to the number 199, then in 33 steps the sequence enters into a loop of three numbers. See Graph 9.2.
Example 9.2.
For
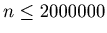 the longest steps to enter into a loop is 58, and one of the number that has the longest steps is 1233466.
the longest steps to enter into a loop is 58, and one of the number that has the longest steps is 1233466.
We are going to present the graph of sequence of numbers in the step to a loop.


: Mathematica Programs
: Curious Properties of Reiterated
: Loops of the Digit