7. The Digit Sum Process Under Mod K.

We are going to study another process. We denote by Mod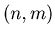$(n,m)$ the residue of n when it is divided by m. For a natural number K we define the dsfK function by

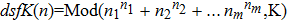
, where 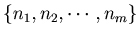$\left\{n_1,n_2,\cdots ,n_m \right\}$ is the list of the digits of an integer n. we start with any positive integer n, and repeatedly apply the function dsfK, then we can generate a sequence of integers .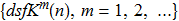
We call the process made by the dsfK function the dsfK process. It is ofthen the case that the dsfK process share many features with the original dsf process, but many theorems are easier to prove in the dsfK when the integer K is small enough. Therefore the dsfK is important for two reasons. One is that we can prove theorems first in the dsfK, and afterwards try to find the same kind of theorems in the original dsf process. The dsfK process gives us the chance to make predictions without using too much time .
The other reason is that it will make a very good courseware for students. Students can enjoy proving many things without worrying about the time and memory they are going to use with their computers.
In a sense this dsfK process is a small universe which shares many theorems with the dsf process which is a bigger universe.
Here we let K = 5000, and we can present interesting facts. We chose 5000, because 5000 is large enough not to make the problem trivial, but small enough to make the calculation easy.

Example 7.1.   If we apply dsf5000 function in Example10.11 to the number 1235 for 40 times, then we get the sequence
{1235, 3157, 1696, 3802, 2248, 2480, 2477, 2346, 1943, 773, 2113, 33, 54, 3381, 2271, 3552, 1281, 2222, 16, 1657, 3325, 3183, 2271, 3552, 1281, 2222, 16, 1657, 3325, 3183, 2271, 3552, 1281, 2222, 16, 1657, 3325, 3183, 2271, 3552, 1281}. By this sequence we can make Graph 7.1.

Graph 7.1.  

If we start with the number 8 and apply dsf5000 function for 40 times, then we get Graphnestdsf5000b.

Graph 7.2.  

To study the loop of dsfK function we use the Mathematica function in Example 10.12.