5. Randomness of the Digit Sum Process.

As you have seen in the previous sections, the digit sum process generated sequences that seems to be quite random. Therefore it is worth while to study the randomness of these sentences statistically.
We have chosen 1000 numbers at random, and for each of these 1000 numbers we get the list of numbers that are in the steps to the loops. We denote the odd number and the even number by 1 and 0, and we look for patterns {{0,0,0},{0,0,1},{0,1,0},{0,1,1},{1,0,0},{1,0,1},{1,1,0},{1,1,1}} in these lists of numbers. Then we have found out that the distribution of these patterns are {4509, 4159, 3862, 4619, 4151, 4398, 4745, 3585} by the Mathematica program in Example 10.10. By this we know that the pattern {1,1,1} is relatively small compared to other patterns, in other words the chance that we have three successive odd numbers in steps is small. Although we have not applied statistical method, the difference is almost clear. In other words this process is not random in terms of odd and even.
If 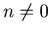$n \neq 0$, then 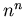$n^n$ is odd or even when 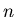$n$ is odd or even respectively, but 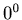$0^0$ is odd when 0 is even. The fact that we use 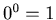$0^0=1$ in Definition 3.1 may have affected the non-randomness of the sequence that the process produces. In the next section we are going to study the process whose definition is different from Definition 3.1.