

: The Digit Sum Process.
: Curious Properties of Reiterated
: The Collatz Problem
We are going to study the DCS (digit cube sum) problem.
Definition 2.1.
We define the dcs function by
,m.gif) , where
, where
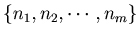 is the list of the digits of an integer n.
is the list of the digits of an integer n.
If we apply dcs(n) function to a natural number n repeatedly, then we get the sequence 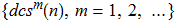 . For the detail of the theory of the DCS problem see [7].
. For the detail of the theory of the DCS problem see [7].
Example 2.1.
For Example, we start with n= 12. Then
dcs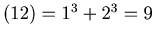 ,
dcs
,
dcs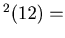 dcs
dcs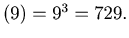 dcs
dcs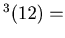 dcs
dcs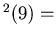 dcs
dcs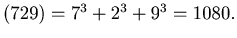 We continue this operation and we get
We continue this operation and we get
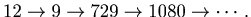
Lemma 2.1.
We have
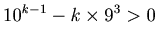 |
(2.1) |
for natural number 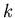 such that
such that 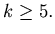
Proof.
Suppose that m has k digits, then
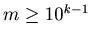 . Since each digit is less than or equal to 9,
dcs
. Since each digit is less than or equal to 9,
dcs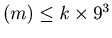 .
By Lemma 2.1 for
.
By Lemma 2.1 for 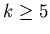 we have
we have
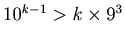 , and hence
dcs
, and hence
dcs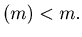
If
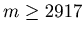 and
and 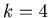 , then
dcs
, then
dcs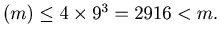
Theorem 1
has been already proved in p.27 of
 .
.
Theorem 2.
For any natural number 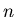 the sequence
the sequence
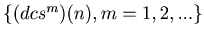 eventually will enter into a loop. In other words there exist numbers p and q such that
eventually will enter into a loop. In other words there exist numbers p and q such that
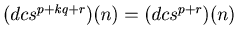 for any natural number k and any integer r such that
for any natural number k and any integer r such that
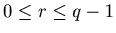 , where we call q the length of the loop. The sequence
, where we call q the length of the loop. The sequence
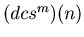 enters into a loop when m = p.
enters into a loop when m = p.
Proof.
If we start with a natural number n, we have a sequence
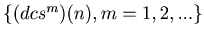 by applying the function dcs to the number n repeatedly. When
by applying the function dcs to the number n repeatedly. When
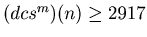 , by Theorem 1
, by Theorem 1
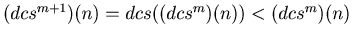 . If
. If
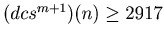 , by Theorem 1 we have
, by Theorem 1 we have
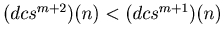 . In this way this sequence decreases while the value of the sequence is bigger or equal to 2917. Therefore there exists a natural number t such that
. In this way this sequence decreases while the value of the sequence is bigger or equal to 2917. Therefore there exists a natural number t such that
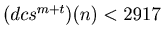 . In this way we can prove that there are infinite number of m such that
. In this way we can prove that there are infinite number of m such that
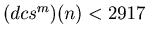 , and hence there is a non-negative integer u such that
, and hence there is a non-negative integer u such that
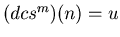 for at least two values of m. Let v be the smallest integer such that
for at least two values of m. Let v be the smallest integer such that
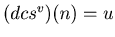 and let w be the second smallest integer such that
and let w be the second smallest integer such that
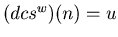 .
.
Then clearly
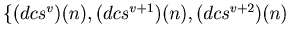 ,...,
,...,
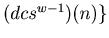 is a loop.
is a loop.
Example 2.2.
If we apply
dcs function to the number 115 for 20 times, then we get the sequence
{115, 127, 352, 160, 217, 352, 160, 217, 352, 160, 217, 352, 160, 217, 352, 160, 217, 352, 160, 217, 352}.
From this sequence we get Graph 2.1.
In Example 2.2 the
dcs function produces a sequence with a loop.
By Theorem 2 successive application of
dcs function will produce a sequence with a loop.
Now we are going to look for all the loops. By Theorem 1 we have only to look for loops of the sequences that start with a number
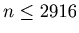 , and we can find loops by calculation of computers.
, and we can find loops by calculation of computers.
Example 2.3.
If we use the Mathematica function in Example 10.3, we can find all the loops. The output of the program is
{{1}, {55, 250, 133}, {133, 55, 250}, {136, 244}, {153}, {160, 217,
352}, {217, 352, 160}, {244, 136}, {250, 133, 55}, {352, 160,
217}, {370}, {371}, {407}, {919, 1459}, {1459, 919}}.
Loops of the length of 3 are {55, 250, 133},{160, 217,
352}, and loops of the length of 2 are {136, 244}, {919, 1459}.
Fixed points are {1}, {153}, {370}, {371}, {407}.


: The Digit Sum Process.
: Curious Properties of Reiterated
: The Collatz Problem
![]() . For the detail of the theory of the DCS problem see [7].
. For the detail of the theory of the DCS problem see [7].