Beautiful Designs made from the Knight's Tour.
Yuya Kakoi,Naoki Saida,Kazuki Takeshima,Yoshiaki Ohishi, Hiroshi Matsui,Toshiyuki Yamauchi, Takashi Kajimoto, Kanta Yoza, Akihiro Hyogu, Yuta Nakagawa, Naoyuki Totani, Daisuke Minematsu and Ryohei Miyadera
miyadera1272000@yahoo.co.jp
1. Introduction.
We are going to present beautiful graphs that were made from the boards of variants of the Knight's Tour.
Traditionally the Knight's Tour consists of moving a knight on a chessboard. The knight is placed on a empty chessboard and, moving by the rules of chess, must visit each square exactly once.
It is possible to define the Knight's Tour on any other grid.
In our variant of the Knight's Tour we do not use a chessboard, and we are going to use the following boards with a wide varieties of shapes.
We can make many beautiful graphs from these boards.
It is very interesting that boards that permit the Knight's Tour often present very beautiful graphs.
First we are going to start with an example.
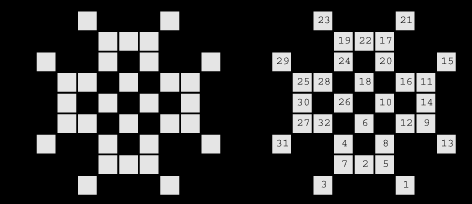
Example 1. How can the knight visit each square on this board exactly once?
The left board is the problem, and the right board shows the answer.

You can make a graph from this board by the following mathod.
The above board consists of 32 squares. We represents these 32 squares by 32 vertexes. We connect corresponding two vertexes by an edge if and only if the Knight can go from one square to another directly. We color a vertex with yellow and an edge with
blue. With a background of black color the graph looks quite beautiful.
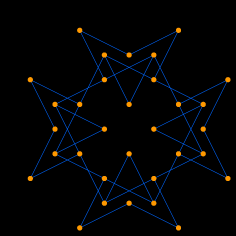
This problem of the Knight's Tour is equivalent to finding a Hamiltonian
path of the graph.
If the final position is a knight's move away from the first postion, we call the tour re-entrant. The tour that is re-entrant is a Hamiltonian circuit of the graph.
Example 2. The left board is the problem, and the right board shows the answer.
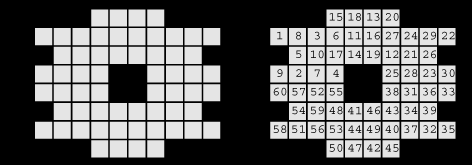
You can make a beautiful graph from this board by the same procedure we used in Example 1.
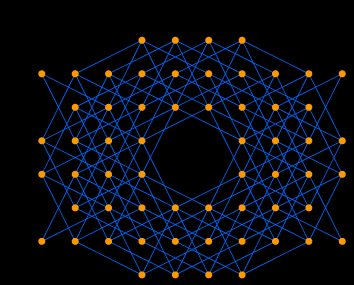
We studied the Knight's Tour problem with a purpose that is different from that of ordinary researchers of the Knight's Tour.
We looked for boards that gave us beautiful graphs.
We are going to show some beautiful graphs without the boards that produced
them.
If you want to see the boards, please read Section 5.
Graph 1.
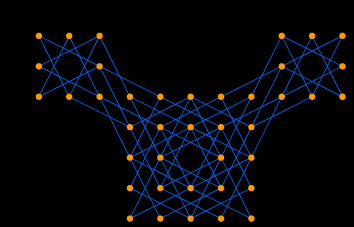
Graph 2.
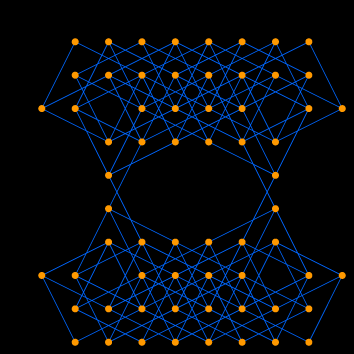
Graph 3.
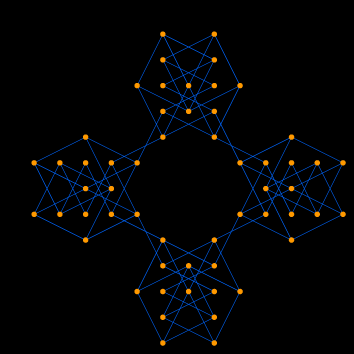
Graph 4.
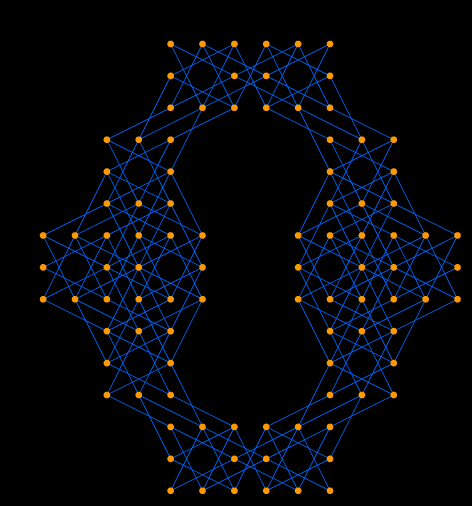
Graph 5.
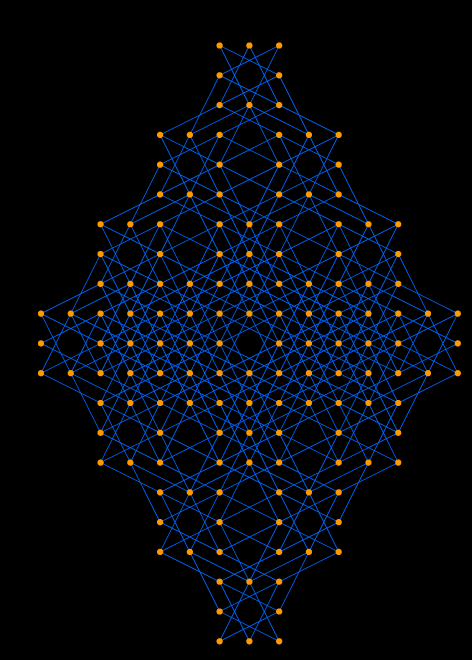
Example 3. We can generalize the Knight's Tour.
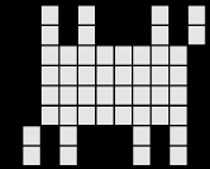
If we use two Knights, then we can use two boards that are mutually disjoint.
The left board is the problem, and the right board shows the answer. One Knight moves on the white squares, and the other on the gray squares.
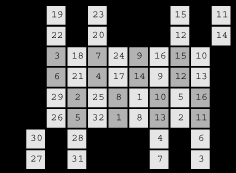
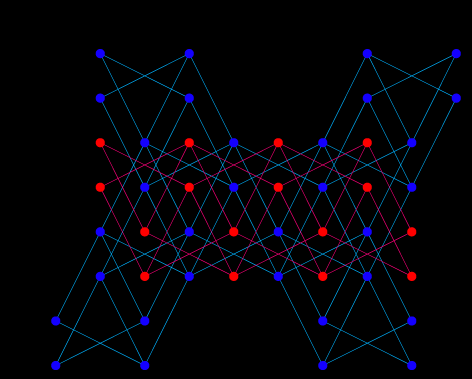
We connect two corresponding blue vertexes with a light blue edge if and only if the Knight can go from one square to another directly, and do the same thing for red vertexes with a purple edge. Then you get the following graph.
We found out that a graph that are made from two Knight's tour can be very
elegant.
Go to Section 2 "A Gallery of Graphs Part 1".
Go to Section 3 "A Gallery of Graphs Part 2".