Isohedrally compatible tilings

Philip M. Maynard 
School of Mathematics, University of East Anglia,
Norwich, NR4 7TJ, United Kingdom. 

Philip_maynard@hotmail.com



 
 
 

Abstract: Two of the 17 (plane) crystallographic groups, G and H, are isohedrally compatible if there exists a tile which admits separate tilings with respective automorphism groups G and H. The purpose of this article is to show that of the 136 possible pairs, 77 are definitely compatible, 44 are not and we conjecture the remaining 15 pairs are also not compatible.

1.  Introduction to isohedral tilings

A tessellation or tiling is simply a covering of the plane by "tiles" which leave no gaps or overlaps. For technical reasons we must be fairly precise by what we mean by tiles. In particular we only consider tiles whose boundary curve is a single, simple (non-intersecting), closed curve (in essence a "loop"). Further, we assume that all our tiles are unmarked i.e. no motif has been drawn on them. An isometry is any mapping of the Euclidian plane E2 into itself which preserves distance. It is well-known that there are only four types of isometry different from the trivial isometry, the identity map. First, there is translation in a given direction by a given distance. Second, we have rotation about a point called the centre of rotation. Next reflection through a line referred to as the line of reflection. A glide-reflection consists of reflecting through some line which we call a line of glide-reflection and then translating parallel to this line some set distance. For a given tiling the set of all isometries which leave the tiling invariant form an algebraic structure called a group. Indeed, this is referred to as the group of symmetries, or automorphism group of the tiling. We can now define two important classes of tilings. 

Definition: A tiling is called periodic if the automorphism group contains non-parallel translations. 

Definition: A tiling is called isohedral if the automorphism group is transitive on tiles. Specifically, if for any two tiles x and y in the tiling there is a symmetry of the tiling which takes x onto y. 

Hence in an isohedral tiling there is essentially just one type of tile. An isohedral tiling is necessarily periodic, (this follows, for instance, from the classification of isohedral tilings given in [2]). We now assume that we have a periodic tiling and we wish to establish its automorphism group. It is a surprising fact that there are only 17 different possible automorphism groups arising from periodic tilings, the so-called (plane) crystallographic groups or wallpaper groups. We shall describe a simple procedure which allows us to differentiate among the 17 groups. Imagine a blank transparency covering the tiling and mark on it the following symbols: a small regular n-gon at every centre of rotation of order n (for n = 2 we use a diamond shape), a solid line at each line of reflection, and a dashed line at each line of glide reflection. It is sufficient to do this only on a small portion of the tiling. What you have now is a blueprint for the automorphism group of the tiling. It is now a simple matter of checking this against a list containing all 17 possible blueprints to determine the automorphism group of your tiling. We note that you may need to rotate, re-size or stretch your blueprint to match exactly the ones in the list. We now present the complete list of 17 different blueprints representing the automorphism groups. In practice this procedure can often be done mentally. A more complete discussion of this section can be found in chapter 1 of [2], where essentially we have taken our list, Figure 1. See also [3] for general reference. 

Finally, we define compatibility. Let P and Q be any two of the 17 (plane) crystallographic groups or wallpaper groups. We call P and Q isohedrally compatible, or just compatible, if there exists a tile T which admits both an isohedral tiling whose automorphism group is isomorphic to P and an isohedral tiling whose automorphism group is isomorphic to Q. Here we are assuming that the tile T is unmarked. We investigate this concept in the next two sections. 

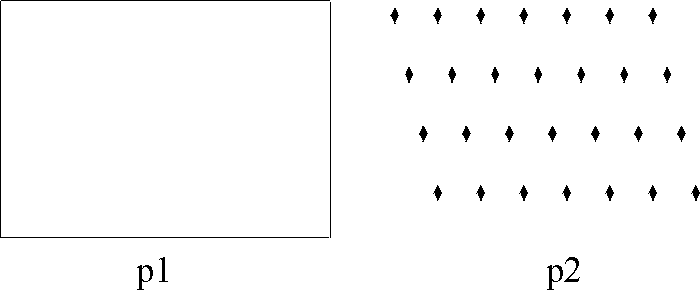
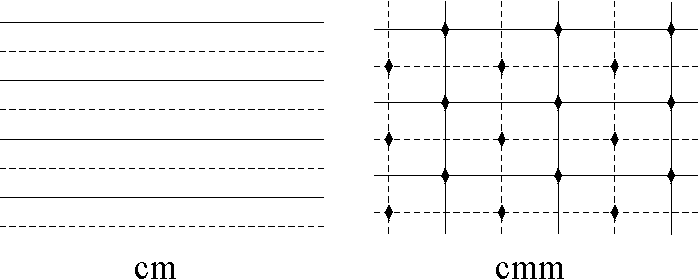
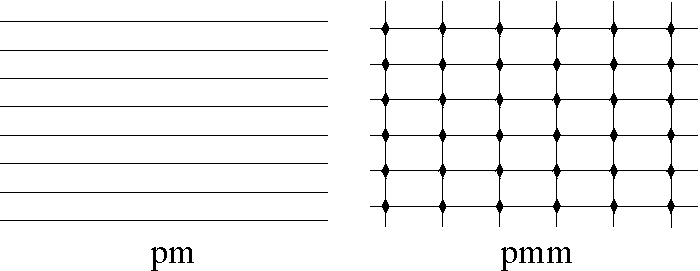
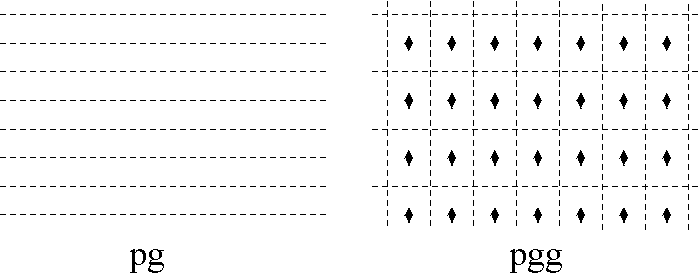
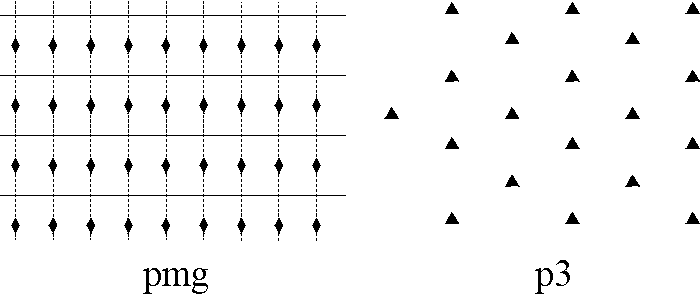
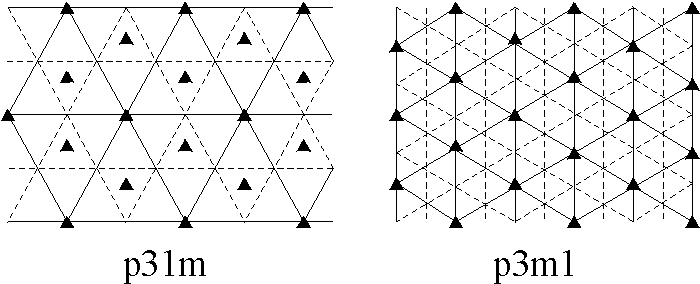
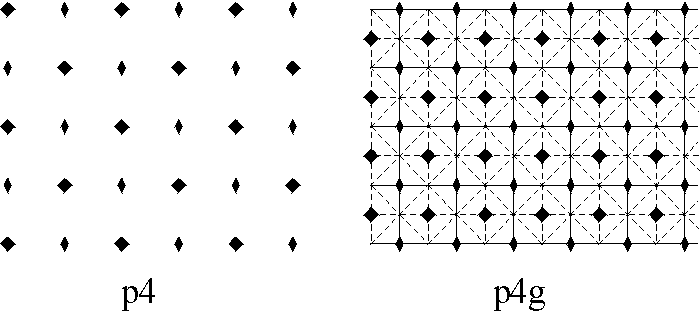
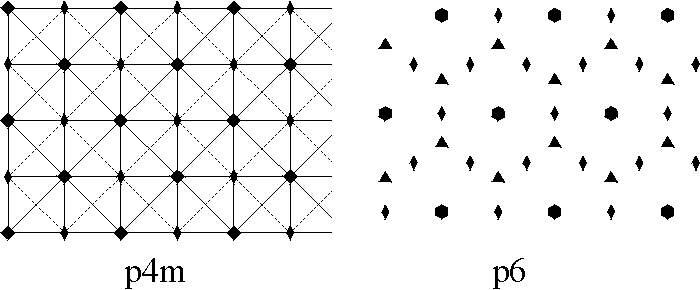
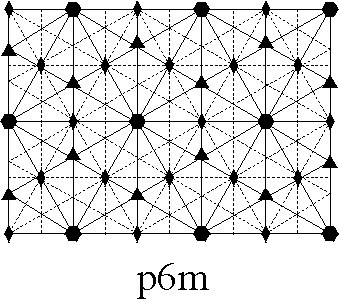
Figure 1: Exhibits all the possible "blueprints" for 
the automorphism group of any periodic tiling.

Example: We present an example of an isohedral tiling which has automorphism group pgg. 

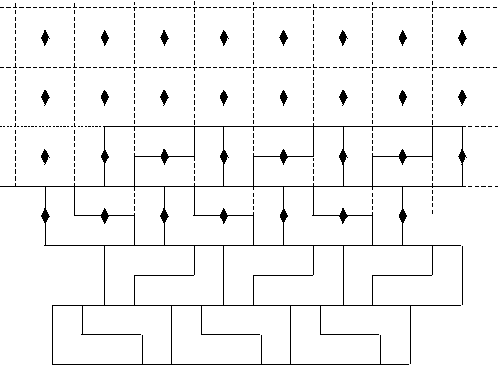
Figure 2: An example of determining the automorphism group of a tiling.



2.  Isohedral compatibility: the exceptional cases

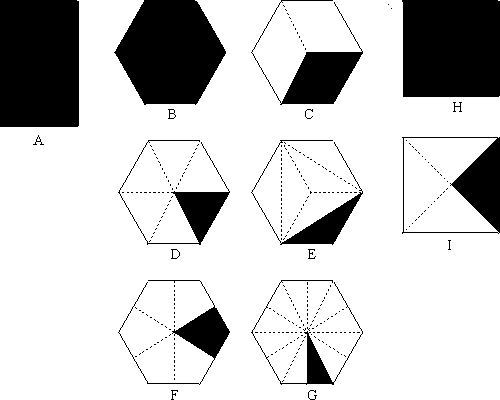
In this section we use the classification of isohedral tilings given in chapter 6 of [2]. First, it follows that the group p3m1 is not isohedrally compatible with any of the other sixteen crystallographic groups. This is since it is not the automorphism group of any isohedral tiling using an unmarked tile. Further, since reflections in the automorphism group of a tiling must have their main lines lie on edges of tiles or bisect tiles, there is only a very limited number of unmarked tiles for which there are isohedral tilings that have p4m, pmm or p6m as automorphism groups. These tiles are shown in Figure 3. (We note that tile A is representative of all non-square rectangles.) 

Figure 3: Shows all the possible tiles (solid) that 
admit isohedral tilings with automorphism groups 
p4m, pmm or p6m.  (A for pmm, B, C, D, E,
F and G for p6m and H and I for p4m).

The justification of this is as follows. We look at the complete list of unmarked isohedral tiles given in [2] for the above groups and inspect their incidence symbols. In particular we look at IH72, IH76, IH82, IH20, IH32, IH37, IH40, IH77 and IH93. For example, for IH32 we have the incidence symbol [a+a-b+b-;a-b-]. All tilings of the same type are obtained by manipulating the edges using a procedure given in [2, p.279] and by altering the lengths or position of edges. All the incidence symbols we are looking at have the following property: any two edges which abut each other either have the same label but orientated in the opposite direction or have the same label and are unorientated. The procedure in [2] then dictates that for all the incidence symbols we are interested in we must leave the edges as straight lines, i.e., we may only distort the tilings by altering the lengths or positions of edges so long as the symmetries of the tiling are not affected. This is only possible in the case of IH72 and this results in a tiling by rectangles. In all other cases we just "enlarge" or "shrink" our tiling. 

We can now determine which of the other 16 crystallographic groups can be isohedrally compatible with the groups p4m, pmm and p6m. To establish this it is simply a matter of determining all the possible isohedral tilings using the tiles in Figure 3. By considering all such possibilities it turns out that it is sufficient to exhibit all isohedral tilings of the tiles I, A and C (the other tiles add no new automorphism groups); we show these tilings in Figure 4, 5 and 6, respectively. 

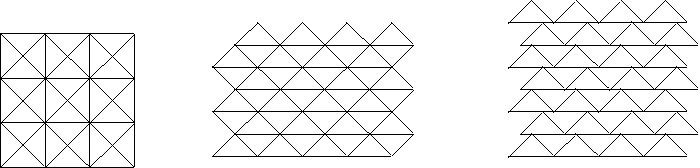
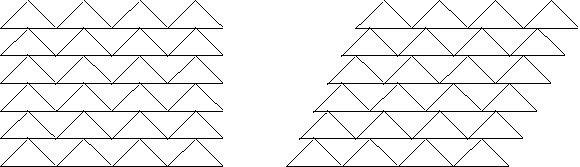
Figure 4: Exhibits all the possible symmetry groups 
with isohedral tilings using the tile I of Figure 3: 
p4m, cmm, pgg, pmg, p2.

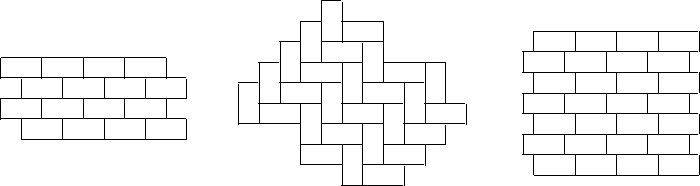
Figure 5: Exhibits all the possible symmetry groups with 
isohedral tilings using the tile A of Figure 3: 
pmm, p2, p4g, cmm, pgg, pmg.

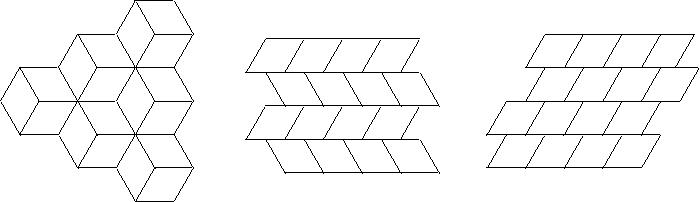
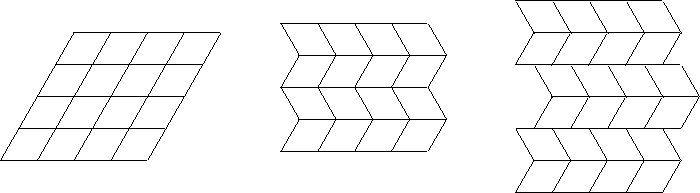
Figure 6: Exhibits all the possible symmetry groups with 
isohedral tilings using the tile C of Figure 3: 
p6m, pgg, p2, pmm, pmg, cm.

We summarize the results of this section in a lemma. 

Lemma 1. The group p3m1 is not isohedrally compatible with any of the other 16 crystallographic groups. Let G1 be isohedrally compatible with p4m then G1 @ cmm, pmg, p2 or pgg. Let G2 be isohedrally compatible with pmm then G2 @ p2, p4g, cmm, pgg or pmg. Let G3 be isohedrally compatible with p6m then G3@ pgg, p2, cmm, pmg or cm.
 
 

3.  Isohedral compatibility: the general case

There are 13 groups left to consider. That is, a possible 78 different compatible pairs. It would appear that some pairs are not possible, however it seems very difficult to show this is the case. We are resigned therefore to presenting examples of tilings that show there are at least 63 compatible pairs. Our results are then summarized in an incomplete table. We begin with a tile which admits isohedral tilings with the following automorphism groups: p1, pmg, p2, pg, pgg, cm, cmm, p4g, p4, (see Figure 7). This accounts for 36 compatible pairs. 

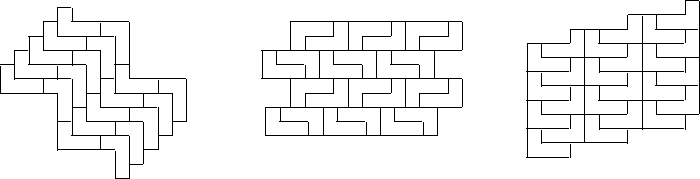
Figure 7: Exhibits isohedral tilings with the following automorphism groups:
p1, pmg, p2, pg, pgg, cm, cmm, p4g, p4.

We now present tilings with a tile that admit the following groups of automorphisms: p1, p2, pgg, cm, pmg, pm, pg, (see Figure 8). This gives 6 additional compatible pairs that include pm. 

Figure 8: Exhibits isohedral tilings with the following automorphism groups:
p1, p2, pgg, cm, pmg, pm, pg.

Figure 9 exhibits tilings with the following automorphism groups: pg, p2, p1, p3, pgg, and gives 4 new compatible pairs that include p3. 

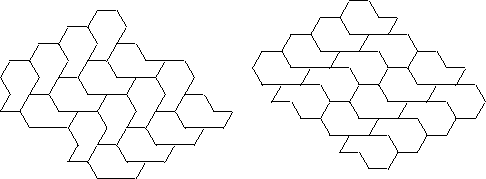
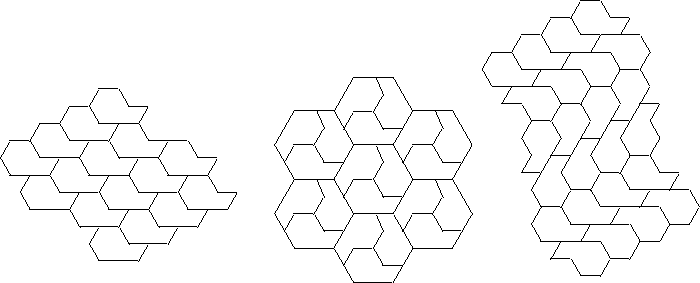
Figure 9: Exhibits isohedral tilings with the following automorphism groups:
pg, p2, p1, p3, pgg.

The next example, Figure 10, shows a tile that admits 8 different isohedral tilings, and adds 13 new compatible pairs that include p6 or p31m. 

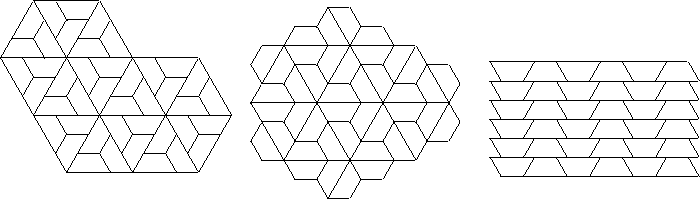
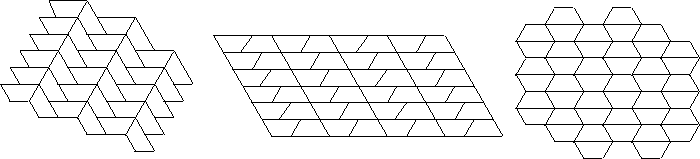
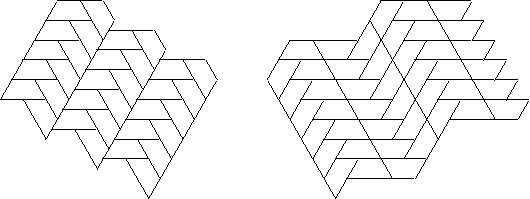
Figure 10: Exhibits isohedral tilings with the following automorphism groups:
p6, p31m, pmg, cm, p2, cmm, pg, pgg.

The tile in the next example has many different isohedral tilings but we show only the three that give us 2 new compatible pairs that include p6. 

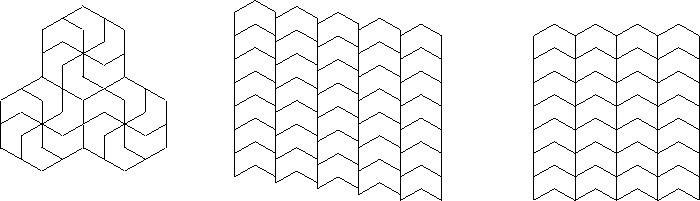
Figure 11: Exhibits isohedral tilings with the following automorphism groups:
p6, p1,pm.

The next example shows isohedral tilings with the same tile and automorphism groups p3 and pmg, respectively. Finally, Figure 13 shows isohedral tilings admitting automorphism groups p1 and p31m, respectively. Each of these examples adds one new compatible pair of groups to our list.

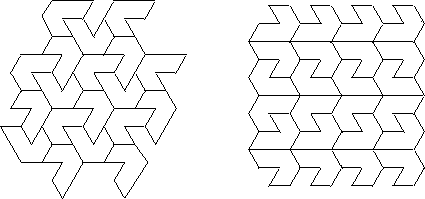
Figure 12: Exhibits isohedral tilings with the following automorphism groups:
p3, pmg.

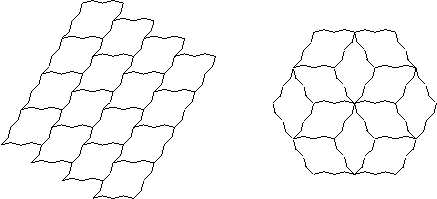
Figure 13: Exhibits isohedral tilings with the following automorphism groups:
p1, p31m.

We summarize our results in Table 1. A "yes" shows that the two groups are isohedrally compatible and a question mark means the question is unresolved. 

p1 pg p2 pgg pmg cm pm cmm p4 p4g p3 p31m p6
p1 yes  yes  yes  yes  yes  yes  yes  yes  yes  yes  yes  yes
pg yes  yes  yes  yes  yes  yes  yes  yes  yes  yes  yes
p2 yes  yes  yes  yes  yes  yes  yes  yes  yes  yes
pgg  yes  yes  yes  yes  yes  yes  yes  yes  yes
pmg  yes  yes  yes  yes  yes  yes  yes  yes
cm yes  yes  yes  yes  ?  yes  yes
pm ?  ?  ?  ?  ?  yes
cmm yes  yes  ?  yes  yes
p4 yes  ?  ?  ?
p4g ?  ?  ?
p3 ?  ?
p31m yes
p6

Table 1: Isohedral compatibility between 13 of the crystallographic groups.


4. Remarks

Obviously, it would be nice to complete Table 1. After searching the author conjectures that crosses (not possible) should replace all the question marks. We note that the problem considered here is related to numerous other (broader) questions, (many not completely solved). For example, given a tile how many different ways can it tile the plane? In general this is unsolvable, even for simple tiles such as polyominoes, see [2]. There are also many obvious ways of modifying the definition of compatibility; for instance, we may weaken it by looking at monohedral tilings or marked tiles. In the former case Grünbaum and Shephard have shown that the 30-60-90 triangle can be used in monohedral tilings with (at least) 14 of the 17 crystallographic groups, see [1]. More generally, we may ask about the compatibility of the 81 different isohedral types. For example, the tilings in Figure 13 are of types IH36 and IH1, respectively. We might also consider higher dimensional crystallographic groups. 

The author has produced many "Escher-type" symmetry pictures, (isohedral tilings using recognizable shapes for the tiles). It seemed a natural challenge to produce recognizable tiles, which can be used in isohedral tilings with 2 (or indeed more) symmetry groups. The author has produced many such examples (Figs. 14, 15, 16). 

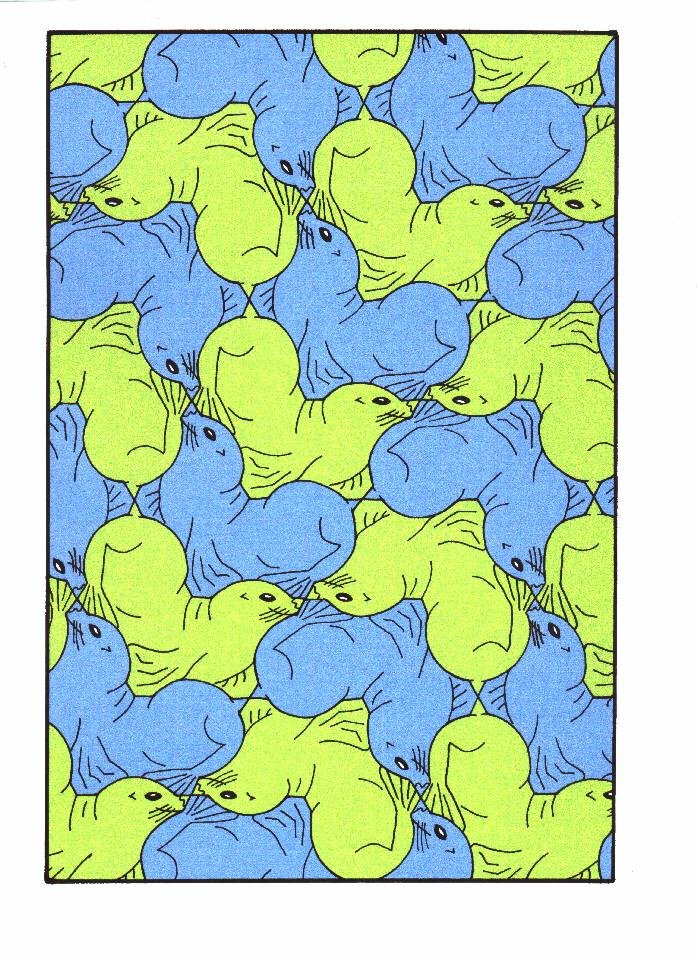
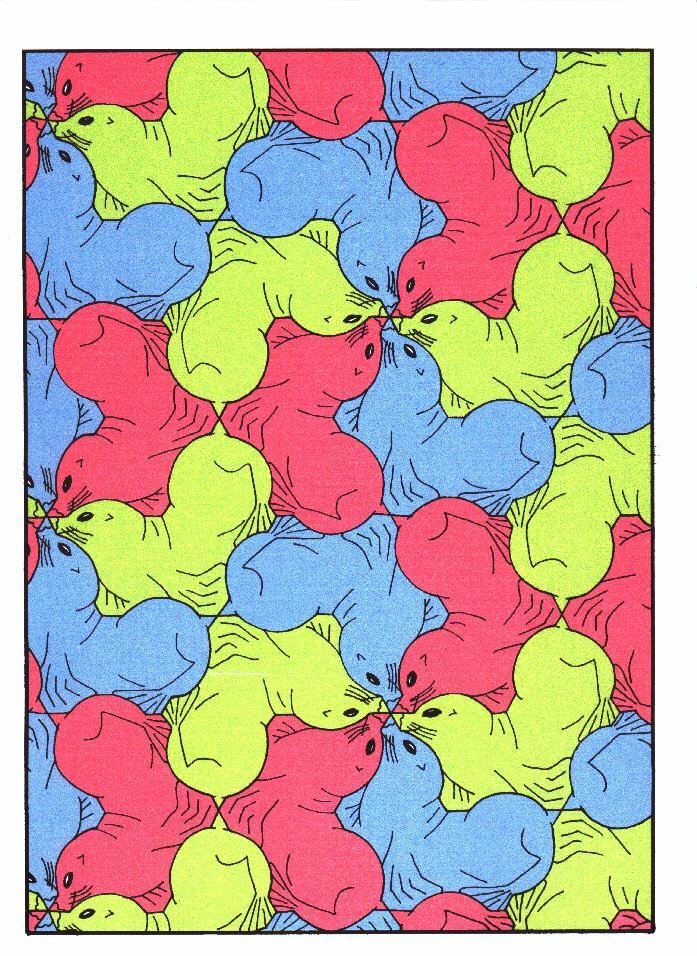
Figure 14: "Sealion", symmetry group p1, pg, pgg, p6.

Figure 15: "Skater", symmetry group p1, p3.

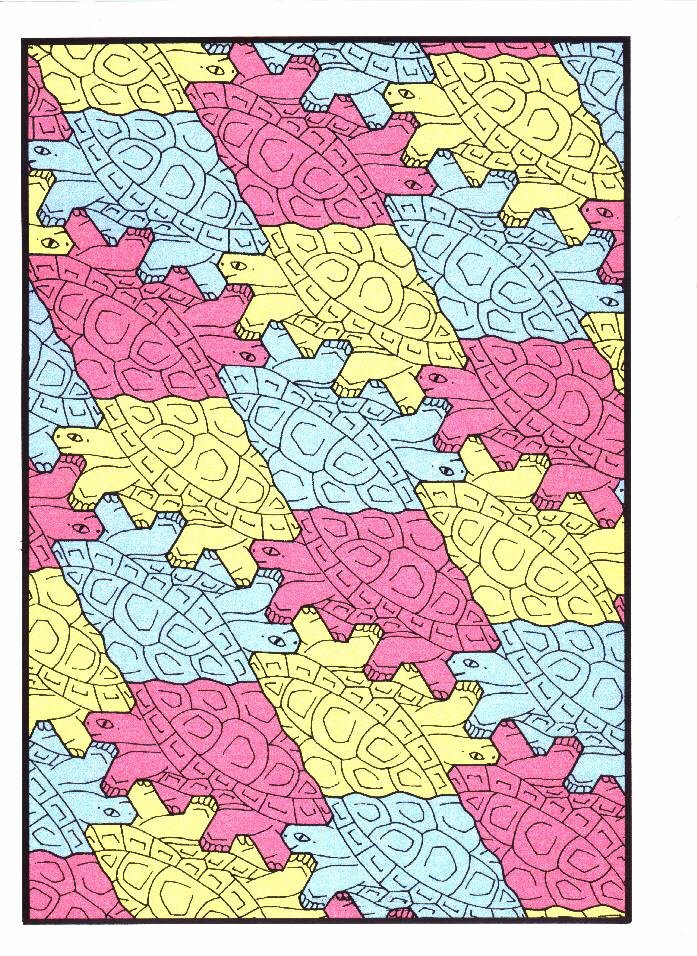
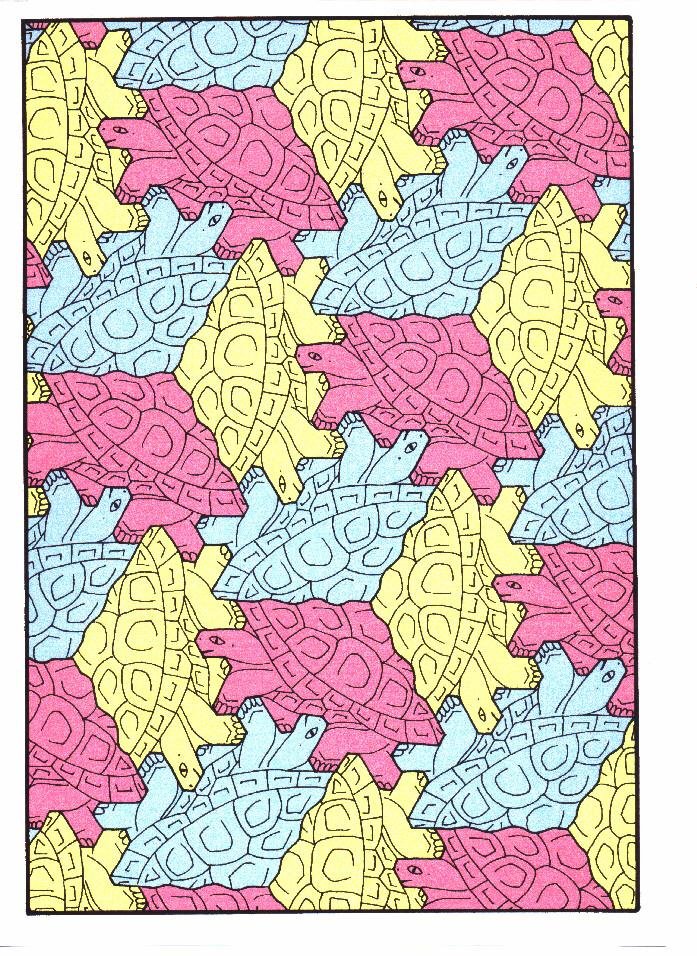
Figure 16: "Tortoise", symmetry group p2, p3.



Acknowledgements

I would like to thank Professor Grünbaum for his helpful correspondence and review of this work. 

References

[1]
B. Grünbaum and G.C. Shephard (1986), Is there an all-purpose tile? Amer. Math. Monthly 93, 545-551.
[2]
B. Grünbaum and G.C. Shephard (1987), Tilings and Patterns, Freeman.
[3]
D. Schattschneider (1978), The Plane Symmetry Groups. Their recognition and notation. Amer. Math. Monthly 85, 439-450. 
VisMathHOME