|
G. Lucca Italy
1. INTRODUCTIONSeashells may be considered a connection point among geometry, mathematics and art. In fact, since ancient times, seashells have always fascinated human kind for their beauty, elegance and, in many cases, symmetry; in particular, this last aspect can be an invite to describe seashells surface by a means of a suitable mathematical model and to visually represent it by the aid of the computer. The first studies on seashells model are due to Reverend H. Moseley [1] and to D'Arcy W. Thompson [2] who emphasized the gnomonic properties and the role of the equiangular (logarithmic) spiral of many seashell species during the growth process. More recent contributions are the ones of D.M. Raup [3], M. B. Cortie [4], [5], C. Illert [6], [7] and D. Fowler et al. [8]. On
the basis of those works, the next paragraphs are devoted to shortly describe
the algorithm for the seashells surface representation and to present some
examples of applications.
2. THE MODEL2.1
Structural curve and Frenet frame
The
first step is to define a Cartesian coordinate system xyz in the
space whose origin is O and characterized by unit vectors i,
j,
k
respectively (see
Fig.1); let us define, with respect
to that system, a curve in the space whose name is
structural curve,
which is strictly related to the overall shape of the seashell. (In many
seashells species the structural curve is represented by the equiangular
spiral in the space i.e. the helico-spiral). It is convenient to represent
the structural curve in parametric form where the parameter is the azimuth
angle q that is:
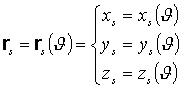 (1)
(1)Related
to the structural curve, we introduce the relevant Frenet frame i.e. an
orthogonal coordinate system characterized by the unit vectors t,
n,
b
(see Fig.1) given by the equations:
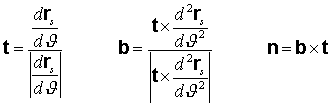 (2)
(2)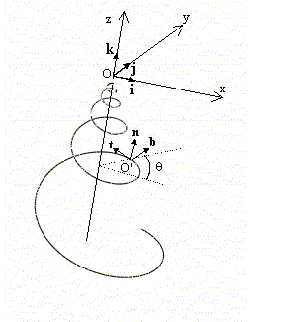
Fig.1: Structural curve (in this case an helico-spiral) and associated Frenet frame.
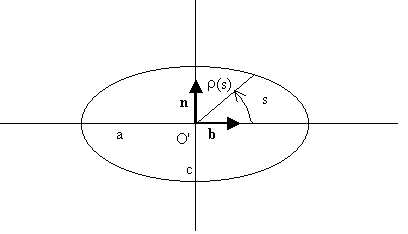
2.2 Generating curve The
second curve that is necessary to introduce is the generating curve
which is strictly related to the shape of the seashell aperture; in most
of cases, an ellipse or an arc of ellipse, with center in O' (the
origin of the Frenet frame) can be a convenient choice. By expressing the
ellipse in parametric form with the angular parameter s as shown
in Fig.2, with respect to the Frenet frame, we
have:
being
(s) given by:
with
a
and c major and minor semi-axes of the ellipse respectively.
Fig.2: Generating curve expressed with respect to the Frenet frame. For the following, it is convenient to represent the generating curve with respect to the fixed system xyz with origin in O; thus, by considering the linear transformation which transforms the unit vectors b into i, t into j and n into k respectively, we have:
We emphasize that in this case the generating curve is also function of the parameter q just because the orientation of the Frenet frame along the structural curve is a function of q. 2.3 Generation of the surface
The
seashell surface is generated by simply translating the generating curve
along the structural curve and, at the same time, by dilating it, in order
to model the growth process; such a process occurs, in most of cases, according
to exponential law. Therefore,the seashell surface equations given in function
of the parameters s and q are:
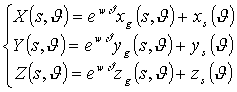 (6) In (6), w is a parameter controlling the exponential growth rate. It
is also possible to model the typical ornamentations present on seashells
surface like ribs, bumps and spikes by introducing a perturbation function
y=y(s,q)
to be added to the function r=r(s) expressed by formula (4).
In such a way, the new following expression for r(s) is obtained:
Without entering into details, we only add that suitable forms for y=y(s,q) are sinusoidal functions (for modelling ribs) or bell-shaped functions (for modelling bumps); the parameters characterising such functions clearly influence the aspect, not only of the ornamentations themeselves, but also of the whole seashell surface. 3. EXAMPLES This
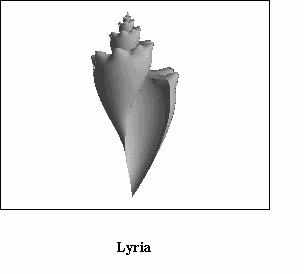
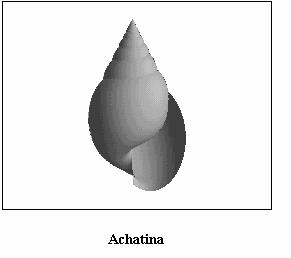
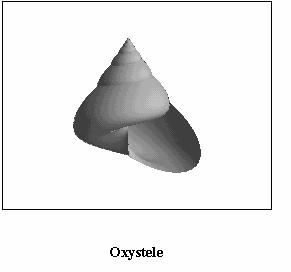
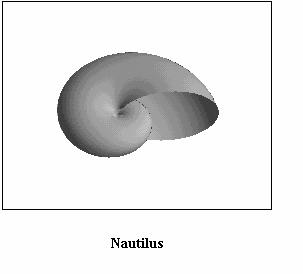
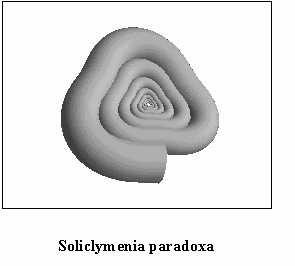
paragraph is devoted to show some examples of real species of seashells
represented by applying the algorithm above described; some among them
are relevant to living molluscs (see Figs. (3), (4),
(5), (6), (7),
(8)) but some other to extinct molluscs i.e. fossils.
(See Figs. (9), (10), (11))
Fig.3
Fig.4
Fig.5
Fig.6
Fig.7
Fig.8
Fig.9
Fig.10
Fig.11
It is useful to mention that Figs. from 3 to 8 are based on a structural curve that, in all the cases, is represented by an helico-spiral (or, as a limit case, a plane equiangular spiral); the consequence is that the seashells exhibit a self similarity property during the growth i.e. the shape of the seashell does not change during the mollusc life but only changes its size. On
the contrary, Figs from 9 to 11 represents seashells
of heteromorphic molluscs; in those cases the structural curve is not an
helico-spiral and thus the self similarity property is not present; this
is particularly evident by looking at Figs 9 and 11.
REFERENCES [1] H. Moseley: On the geometrical forms of turbinated and discoid shells, Philosophical Transactions of the Royal Society of London, Pt I, p. 351-370, 1838. [2] D'Arcy W. Thompson: On Growth and Form, University Press, Cambridge, 2nd Edition, 1942. [3] D. M. Raup: Geometrical analysis of shell coiling: general problems, Journal of Paleontology, vol. 40, no. 5, p. 1178-1190 September 1966. [4] M. B. Cortie: Models for mollusc shell shape, South African Journal of Science, vol. 85, p. 454-460, July 1989. [5] M. B. Cortie: Digital Seashells, Computer & Graphics, vol.17, no. 1, p. 79-84, 1993. [6] C. Illert: Formulation and Solution of the Classical Seashell Problem. II Tubular Three-Dimensional Seashell Surfaces, Il Nuovo Cimento, vol. 11 D, no. 5, May 1989. [7] C. Illert: Nipponites Mirabilis-A Challenge to Seashell Theory?, Il Nuovo Cimento, vol. 12 D, no.10, October 1990. [8]
D. R. Fowler, H. Meinhardt, P. Prusinkiewicz: Modeling seashells, Proceeding
of SIGGRAPH '92 (Chigago, Illinois, July 26-31, 1992), In Computer Graphics,
26, 2 (July 1992), ACM SIGGRAPH, New York, p. 379-387 (available on line
at the address: http://www.cpsc.ucalgary.ca/Redirect/bmv/papers/shells/sig92.pdf).
|
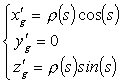 (3)
(3) 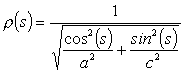 (4)
(4)
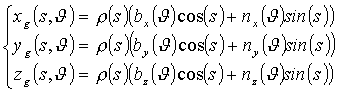
 (7)
(7)