|
Abstract Using a computational procedure that imitates tightening of an assembly of billiard balls, we have generated a number of packings of n equal and non-equal disks in regions of various shapes for n in the range 10 to 10,000. Our experiments revealed various geometric patterns and regular features, including polycrystalline textures with "rattlers'' typically trapped along the grain boundaries. We also observed series of packings with similar patterns for n taking on increasing sequences of values, n = n(1), n(2),... n(k),.... Billiards algorithm
Packings of non-overlapping disks or cylinders can be mechanically generated by tightening the container boundary [7]. A variant of this procedure has been implemented on a computer [4] as a discrete event "billiards'' simulation algorithm [3]. Rather than shrinking the container, in the billiards simulations we uniformly expand the disks. Fig. 1 illustrates the work of the billiards simulation algorithm while packing 2000 equal disks in a square with periodic boundary (torus). The initial stage at time t = 0 is represented on the top square in the figure where 2000 points are randomly scattered. To each point an initial velocity vector is randomly assigned (not shown). Some points lie outside the square; they are periodic images of the corresponding points inside. When t > 0, the points grow into disks, and all disks at each time t have common diameter d = Et. The growth continues until the configuration "jams,'' at which time we expect to have a packing. At t = 0 disks do not overlap because their sizes are zero. For t > 0 disks move along straight lines with given velocities; their motions may conflict with each other. At an instance of such a two-disk conflict, we simulate an elastic collision of these disks assuming their masses are equal. At a collision both disks change their velocity vectors so as to exchange momenta and energies according to known mechanical laws.Note that the evolution of the disk configuration does not change if we proportionally change both the disk expansion speed E and linear disk velocities.We normalize the simulation input by assuming the unity mean initial disk velocity. 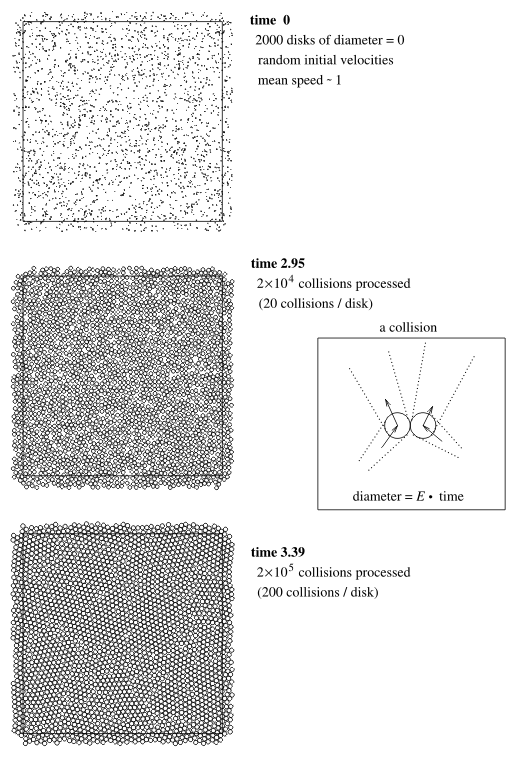
Figure 1: Successive stages
in an instance of disk packing by billiards algorithm.
A number of packings have been produced by randomly varying initial configuration of points, their initial velocity, and the expansion speed E. Packings generated under a high E (in Fig. 2), a moderate E (in Fig. 3), and a low E (in Fig. 4) were obtained. For high E the pattern is a combination of hexagonally packed fragments, "grains,''with each grain having generally different orientation. Irregularity concentrates along the grain boundaries, as do the "rattlers,'' the disks that are not rigidly fixed in their positions but trapped in the cages formed by their fixed rigid neighbors or boundary walls if any.
The size of the grains increases (and their number for a fixed n decreases) as the E decreases. For a sufficiently small E, a single hexagonal "crystal'' emerges. The array of hexagonally packed disks contains interesting structural deviations and insertions.Sometimes the symmetry of the packing coupled with a high value of its density suggests that perhaps we have achieved the optimum, i.e., the packing of the largest possible disk diameter and density. This might be the case in Fig. 4. (The density is the fraction of the region area covered by disks.)
Frustrated packings56 equal disks stacked hexagonally in
8 alternating columns, 7 disks in a column, constitute the optimum packing
in a rectangle with periodic boundary conditions if the ratio of the height
of the rectangle to its width is (1 + 1/48)1/2 = 1.01036...
We frustrate the packing by increasing the width of the rectangle and making
it equal to the height. In the new shape, previously jammed disks become
loose and can grow further to exploit the extra space. As the disks grow,
a new jamming is achieved with a larger disk diameter.
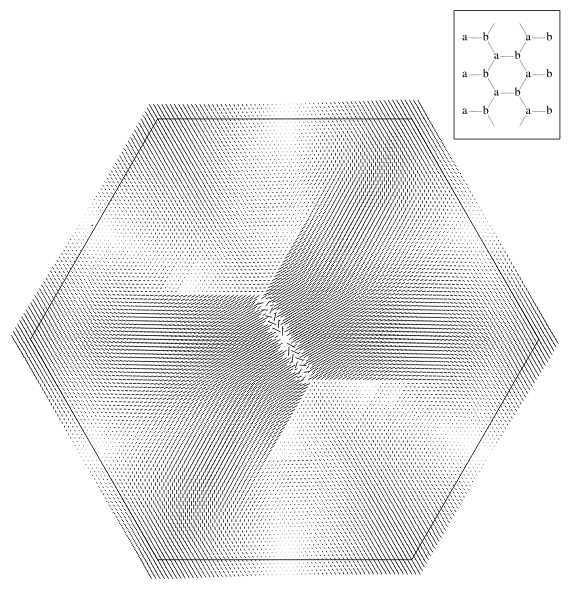
In the example of a frustration in Fig. 6 we begin with a perfectly hexagonally packed configuration of 10,800 equal disks. Note that we can always perfectly pack 3k2 equal disks in a regular hexagon with periodic boundary conditions, as explained in the figure. k disks will fit along each hexagon side. Here k = 60. We uniformly decrease the size of all the disks but one in the center. The diameter of the latter is increased. As a result all the disks become loose. We tighten the configuration by simulating expansion with very small rate E. During the expansion, while diameters of all disks are increasing, we keep constant the ratio of the diameter of the large disk to that of other disks.
As a result, a frustration with a "crack''
centered at the larger disk is developed. To enhance visually the structure
of the frustration, we display disk displacements. Each disk has the "ideal''
position of its center p0 in the original non-frustrated
packing and the final position of the center p1 in the
frustrated packing.Vector p1 - p0 is
the displacement. Accumulation of the round off error may cause the entire
configuration to shift during the expansion. We "calibrate'' the displacement
vectors by subtracting from each of them the displacement of the larger
disk. The latter displacement becomes zero by definition.
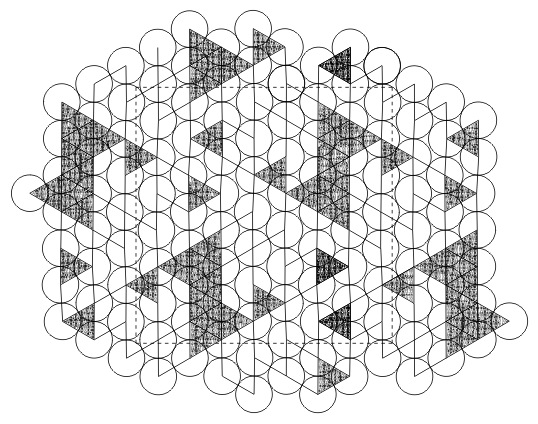
Repeated patterns in packings in equilateral triangle,
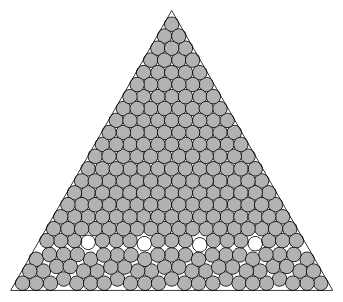
The optimum packing of D(k) = k(k+1)/2 equal disks in an equilateral triangle is the hexagonal arrangement [6] and the optimality holds for all k = 1, 2, .... Are the triangle numbers D(k) the only such lucky sequence? We conjecture the existence of an infinite number of sequences so that each sequence has its own well-defined pattern of optimal packings.
For each p = 0, 1, 2,... consider sequence
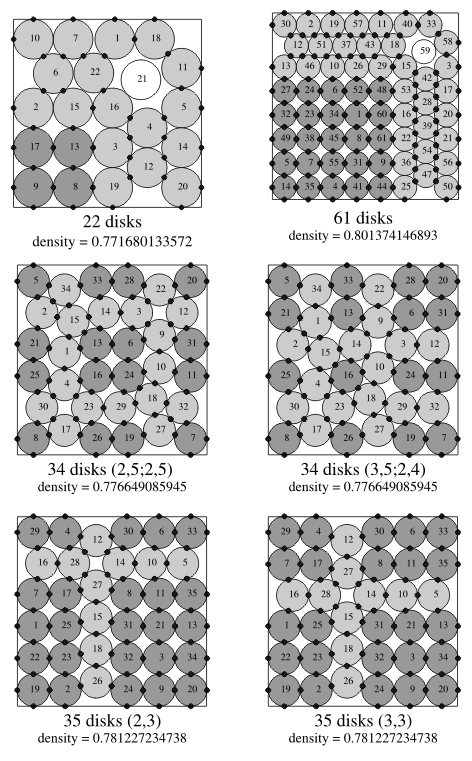
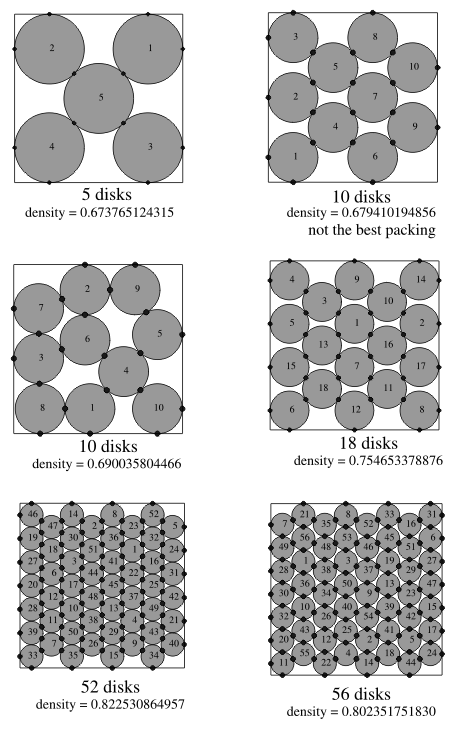
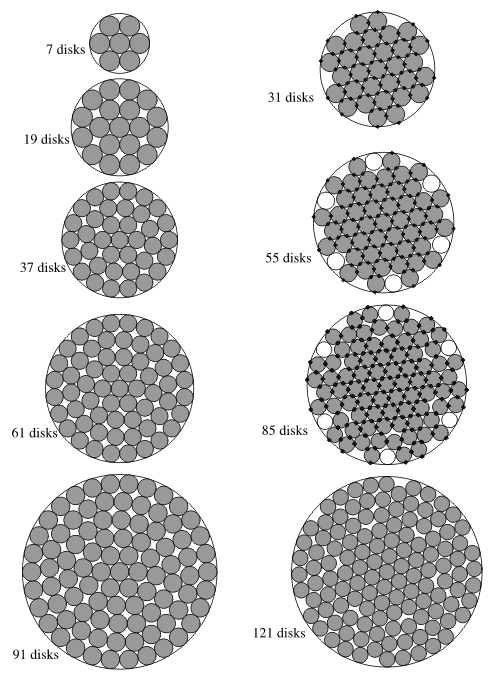
For p = 0 sequence np(k) is identical with the sequence of triangle numbers D(k) with known optimal packings. For each p > 0, we conjecture the optimal packing of np(k) disks as the pattern that consists of n-p+1 solid disks and p-1 rattlers; it includes one triangle of side (k+1)p-1 and 2p+1 alternating triangles of side k each as shown in Fig. 7 for the case p = 5 and k = 3. A k×k orthogonal arrangement is a "natural'' square packing in the same spirit as hexagonal disk arrangement is a natural packing in an equilateral triangle. This square arrangement becomes non-optimal for large k, though. What we observe in the best found packings in the square is an interplay between two patterns: square and hexagonal. For a sufficiently large number of disks n the hexagonal pattern becomes dominant.With the billiards simulation algorithm we were able to examine details of this interplay for small n. The following sequences were recently identified [1, 5] as candidates for pattern repetitions: k2-3, k2 -2,k2-1. These are "frustrations'' of the "natural'' square pattern. Some members of these sequences are presented in Fig. 8. In this and the following figures black dots identify contacts (between two disks in a pair or between a disk and the boundary). Sometimes, disks are seemingly in contact, like disks 2 and 15 in the packing of 22 disks in Fig. 8, but no dot is present in the contact site. This indicates a positive gap between the disks. The gap may be not discernible on the picture, but can be verified computationally. Because a pair of rows and a pair of columns are "frustrated'' in best packings of k2-2 disks (middle row in Fig. 8), the two pairs of indices can identify the packing, like (3,5; 2,4). Sequences k(k+1) and k2+ [k/2] were also identified (where [x] denotes largest integer that is not exceeding x); they can be considered as "frustrations'' of a hexagonal pattern adjusted to the square boundaries. Some of their members are presented in Fig. 9. Note that the best packing of 10 disks does not follow the common pattern of sequence k2+ [k/2]. As in the case of a square, a circle boundary shape does not conform to the hexagonal disk arrangement. Unlike the case of a square or equilateral triangle, no obviously "natural'' packing of equal disks has been proposed. Perhaps, the curved hexagonal packings [2] can be taken as such. They are presented in the left column in Fig. 10. Three different equally dense curved hexagonal packings of 61 disks are known. Fig. 10 presents one of them. Similarly, 12 different equally dense curved hexagonal packings of 91 disks are known and Fig. 10 presents one of them.The curved hexagonal packings of 3k(k+1)+1 disks exist for arbitrary large k but they become not the densest ones for k = 6, 7,... (n = 127, 169, ...). The right column in Fig. 10 presents best found packings for the sequence 3k(k+3)+1. These demonstrate a different way of adjusting hexagonal packing to the circular-wall boundary.
References
|