3. Recursive Pursuit Relative Motions

3.1 Definition

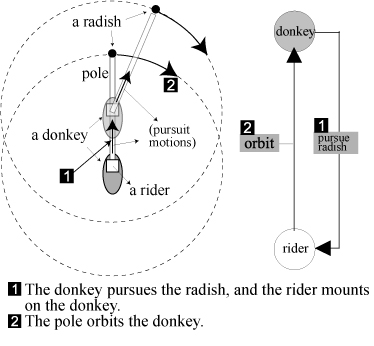
It is difficult to imagine that what kinds structure of relative motion should be, which implement the recursive characteristic into the framework of pursuit motions. We approach to introduce the concept of recursive pursuit motions by means of imagine that a rider mounting on a donkey, and who holds on a pole which hang a radish on it. The pole with hang a radish places in front of the donkey, and entice it to move forward and then eat the radish. The pole orbited the rider who mounted the donkey by a unit of angle variation when the donkey moving forwards a step. That is a repeated cycle for the donkey pursued the radish, and then the pole orbited the rider (also the donkey). Detailed descriptions can be shown as the illustrations of Fig. 10. The position of the donkey should highly influence the absolute coordinate system of the pole, and repeatedly re-influence itself of the donkey. Endless of iterating the recursive pursuit motions, the ultimate trajectories can result in highly unpredictable and peculiar complex patterns.

Fig. 10. Illustrations of recursive pursuit relative motions

3.2 Manipulate the Parameters

We might divide manipulations of the parameters into four implements, and experiment the differences in diversity of related parameters. The combinations for these implements should influence mutually in the same recursive pursuit relative motions. The implements include (1) manipulate the number of recursive pursuit levels, (2) dynamic variations of recursive radius, (3) dynamic ranges of angular increment, and (4) dynamic variations of pursuit velocity.

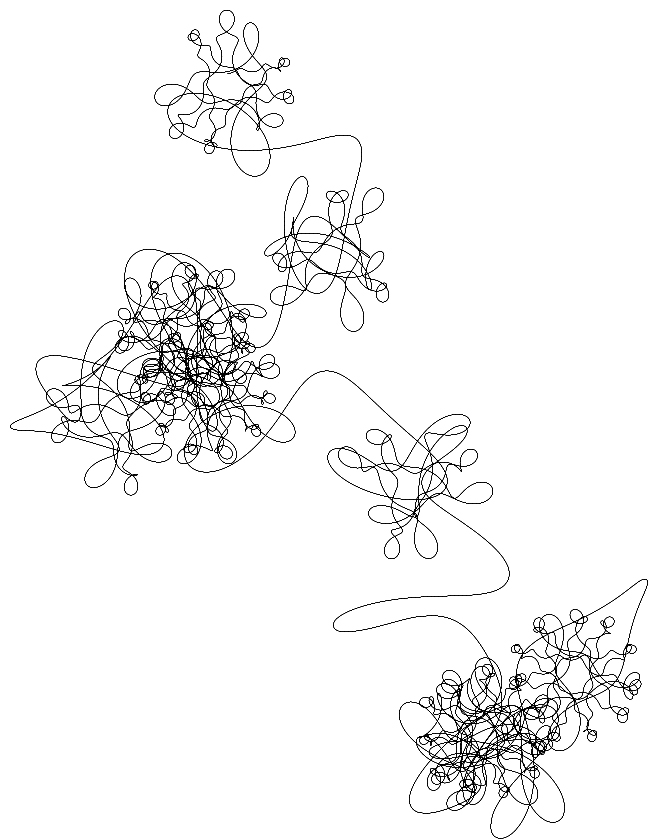
It is apparent that the number of recursive pursuit levels can be unlimited, and more complicated recursive pursuit motions induce the unpredictable and complex patterns. Dynamic variation of recursive radius appears a spiral motion to influence the positions of next iterations. To manipulate the angular increment is an implement that immediately influences the patterns. Angular increment is a constant in general. In order to implement the different orbited velocities between periods of recursive pursuit motions, we can manipulate dynamic range of angular increment to complicate the movements. The manipulated parameters of dynamic ranges include ceiling-limit, floor-limit and slight variations. Pursuit velocity also plays a significant factor that concerns with the appearances of patterns. In recursive framework, the slight variations of pursuit velocity acutely influence the scale of generated patterns, and namely have effects on the scope of movements. It is obviously difficult to experiment the fullness of diversities for manipulated parameters. A series of case studies would be investigated as below discussions.

3.3 Geometric Patterns Design

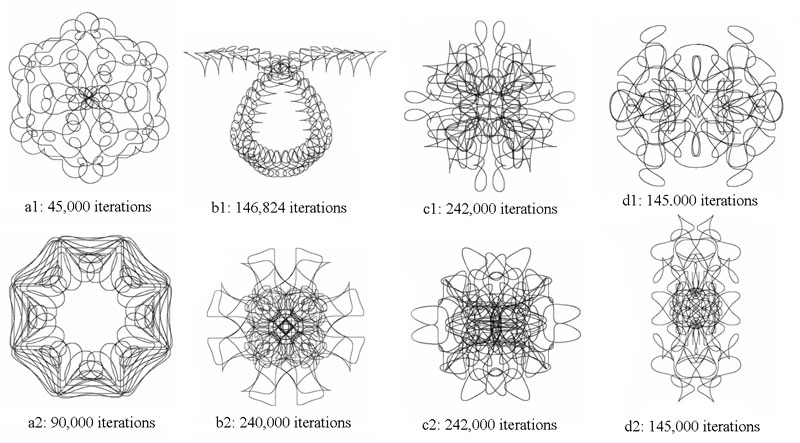
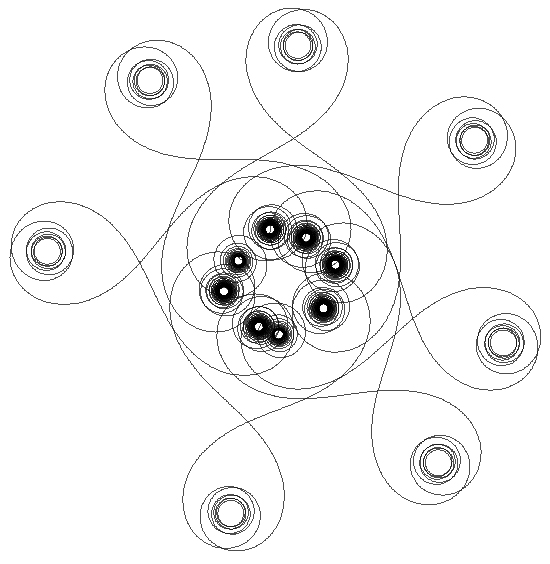
In this section, we experimented some cast studies with manipulate different parameters of recursive pursuit relative motions. The patterns of Fig. 11 were created with 4-RL, 5-RL, 6-RL, and 7-RL. The detailed parameters of Fig. 11 are shown in Tab3. The initiation P₀ always pursues the termination of coordinate system (for * marker), and the pursuit velocity is 0.1 pixels per iteration. Each of recursive radiuses equals 2 pixels.

Fig. 11. The differences in patterns created with the 4-RL, 5-RL, 6-RL, and 7-RL. Detailed parameters show in Tab 3.

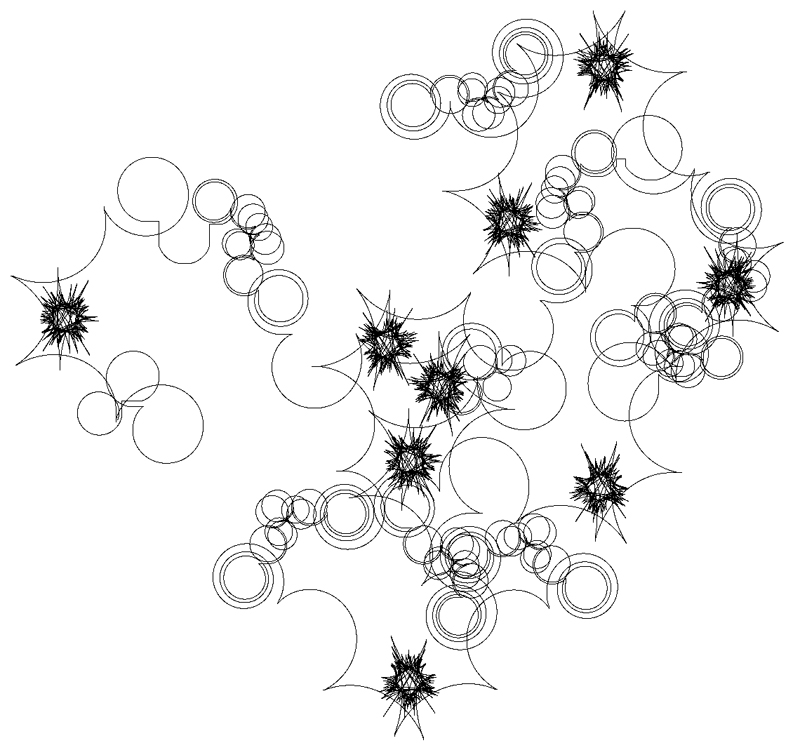
Tab. 4 had showed the detailed parameters of Fig. 12. The patterns of Fig. 12 were created with 3-RL, 4-RL, and 5-RL, and the manipulations of these case studies focused on implementing the slight variations of radius to generate the spiral motions. Furthermore, we had manipulated the termination of coordinate systems to perform the dynamic radius in addition to the case of Fig.12b3 for whole movements appear the spiral motion. The initiation P₀ pursues the termination of coordinate system by 1 pixel per iteration.

Fig. 12. The differences in patterns created with the 3-RL, 4-RL, and 5-RL. Detailed parameters show in Tab 4.

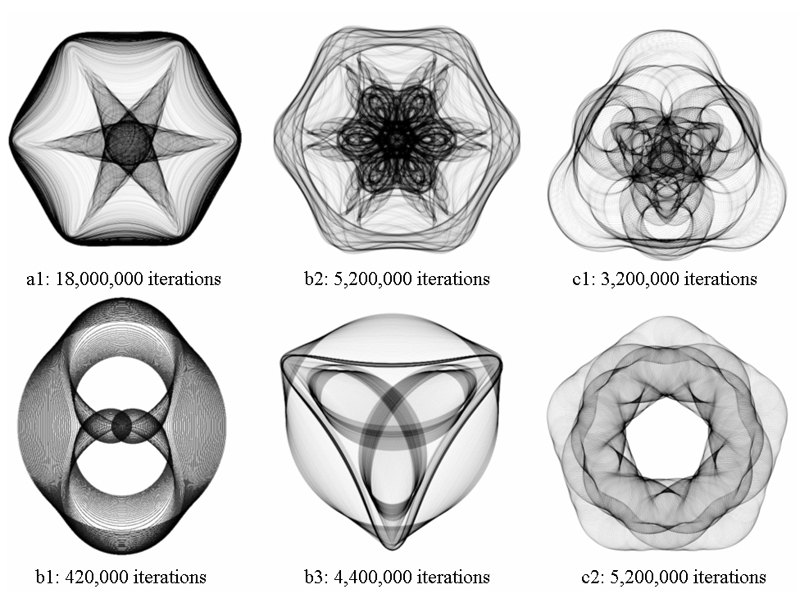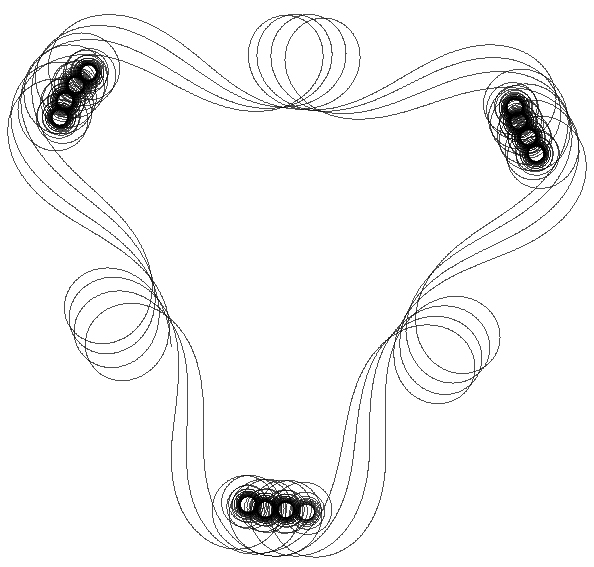
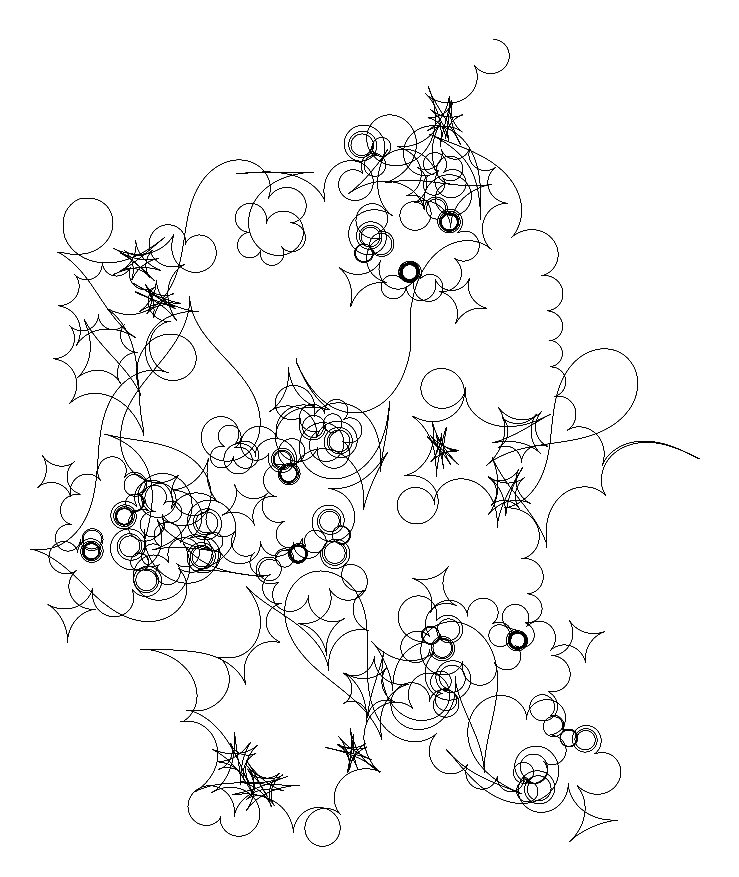
Tab. 5 had showed the detailed parameters of Fig. 13, and the patterns were generated with 2-RL, 3-RL, and 4-RL coordinate systems. The manipulations of these case studies of Fig. 13 concentrated on experimenting dynamic ranges of angular increment. We had manipulated the angular increment(s) of coordinate system(s) to vary from the range between assigned ceiling and floor value. Manipulating the dynamic angular increments is easily to compose the fascinated patterns with peculiar geometric trajectories. The initiation P₀ pursues the terminational coordinate system by 1 pixel per iteration, and then each of recursive radiuses equals 10 pixel.

Fig. 13-a1: 36,000 iterations ( The differences in patterns created with the 2-RL, 3-RL, and 4-RL. Detailed parameters show in Tab 5.)

Fig. 13-a2: 34,000 iterations ( The differences in patterns created with the 2-RL, 3-RL, and 4-RL. Detailed parameters show in Tab 5.)

Fig. 13-b1: 400,000 iterations ( The differences in patterns created with the 2-RL, 3-RL, and 4-RL. Detailed parameters show in Tab 5.)

Fig. 13-b2: 180,000 iterations ( The differences in patterns created with the 2-RL, 3-RL, and 4-RL. Detailed parameters show in Tab 5.)

Fig. 13-c1: 160,000 iterations ( The differences in patterns created with the 2-RL, 3-RL, and 4-RL. Detailed parameters show in Tab 5.)

Fig. 13-c2: 240,000 iterations ( The differences in patterns created with the 2-RL, 3-RL, and 4-RL. Detailed parameters show in Tab 5.)