Group Theory and Architecture, 2:

Why Symmetry/Asymmetry?

Professor Michael Leyton.

Dept. of Psychology, Rutgers University

Introduction

This is the second in a sequence of tutorials on the mathematical structure of architecture. The first was Group Theory and Architecture, 1. The purpose of these tutorials is to present, in an easy form, the technical theory developed in my forthcoming book on the mathematical structure of design.

In this second tutorial we are going to look at the functional role of symmetry and asymmetry in architecture. We are all aware that classical architecture was dominated by symmetry. In contrast, we have seen, in the 20th century, a shift from the dominating role of symmetry to the gradual raising of asymmetry as the major principle. Famous examples of the latter include Frank Lloyd Wright's Falling Water, with its asymmetrically arranged blocks, or Eero Saarinen's TWA Building with its free form structure, or in the contemporary world, the Deconstructivist Architects are now the dominant force. The latter movement came into significant public recognition with the exhibition of their work in the Museum of Modern Art, New York, in1988, and these architects are now the most famous archictects in the world - usually winning the major architecture competitions. They include Peter Eisenman, Zaha Hadid, Frank Gehry, Coop Himmelblau, Rem Koolhaas, Daniel Libeskind, and Bernard Tschumi. In all their buildings, asymmetry is the major organizing factor.

What we wish to consider, in this paper, is the following issue: Why was classical architecture dominated by symmetry; i.e., what purpose did symmetry serve in classical architecture? Correspondingly, why is modern architecture dominated by asymmetry; i.e., what purpose does asymmetry serve in modern architecture?

The answer to this question comes from my previous book Symmetry, Causality, Mind (MIT Press, 630pages), in which I argue that symmetry is always used to erase memory from an organization, and asymmetry is always used to introduce memory into an organization. I show that these memory principles are deeply embedding in the human mind: indeed they are what allows the mind to work. It is these memory principles, I argue, that are at the basis of classical architecture's use of symmetry and the modern architecture's use of asymmetry. That is, classical architecture is aimed at removing memory, and contemporary architecture aims at creating memory.

Inferring History from Shape

The book Symmetry, Causality, Mind  (MIT Press) presents a 630 page rule-system by which the mind extracts the past history that produced a shape, i.e., the sequence of causal forces that produced the shape. Despite the enormous number of rules they all are different forms of only two basic rules: one that exploits the asymmetries in a shape, and one that exploits the symmetries in the shape. The theory ultimately explains how any organization can hold "memory" of past actions.

If we define "memory" to be information about the past, we observe that there are many forms that memory can take. For example, a scar is memory of past events because, when we look at it, we are able to extract information about past actions, i.e., the fact that there had previously been a past cutting action across the skin. Again, a crack in a vase is memory of past events because, when we look at it, we are able to extract information about past actions, i.e., the fact that there had previously been a blow applied to the vase. There are in fact an almost infinite number of forms that memory can take: scars, cracks, dents, twists, growths, and so on. However arguments presented in my book (Leyton, 1992), lead to the conclusion that, on an abstract level, there is only one form that memory takes:

I can give you a simple illustration of this as follows: Imagine a tank of gas on the table. Imagine that the gas is at equilibrium, at TIME 1. The gas is therefore uniform throughout the tank, in particular, symmetric - left to right in the tank. Now use some means to attract the gas into the left half of the tank at TIME 2. The gas is now asymmetric.

Someone, who has not previously been in the room now enters and sees the gas. The person will immediately conclude that the gas underwent a movement to the left. This means that the asymmetric state is memory of the movement. Now let the gas settle back to equilibrium, that is symmetry at TIME 3, that is, uniformity throughout the tank.

Suppose another person enters now, someone who has not been in the room before. This new person would not be able to deduce that the gas had previously moved to the left and returned. The reason is that the symmetry has wiped out the memory of the previous events. The conclusion is that from symmetry, you can conclude only that the past was the same. We can summarize the rules used here, in two principles:

ASYMMETRY PRINCIPLE: An asymmetry in the present is assumed to have been a symmetry in the past.

SYMMETRY PRINCIPLE: A symmetry in the present is assumed to have always existed.

In mathematics, symmetry means indistinguishability under transformations. Thus, for example, a face is reflectionally symmetric because it is indistinguishable from its reflected version, and a circle is rotationally symmetric because it is indistinguishable from any of its rotated versions.

Now, what we will see, over and over again, in this paper, is that the way to used the above two rules is as follows: You first partition the present situation into its asymmetries and symmetries. You then use the first rule on the asymmetries and the second rule on the symmetries. That is, the first rule says that the asymmetries go to symmetries, backward in time; and the second rule says that the symmetries are preserved, backward in time.

Let us now illustrate this: In a converging series of psychological experiments, I showed that, if subjects are presented with the first stimulus shown in the figure below, a rotated parallelogram, they reference it, in their minds, to a non-rotated parallelogram, which they then reference to a rectangle, which they then reference to a square. The important thing to understand is that they are presented with only the first figure; and, from this, their minds generate the sequence shown.

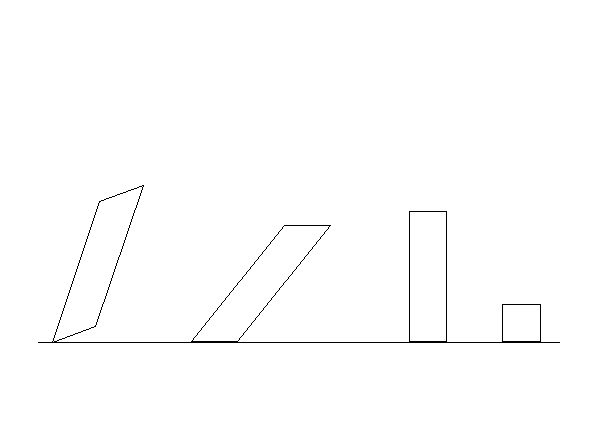One can interpret this data by saying that, given the initial object, subjects are inferring the process-history that produced it. That is, the presented object was produced by starting with a square, stretching it, then shearing it, and then rotating it. We shall now see that what the subjects are doing is using the Asymmetry Principle and Symmetry Principle. To see this, we must, as I said, first partition the presented shape - the rotated parallelogram - into its asymmetries and its symmetries. Consider first the asymmetries. There are in fact three of them: (1) the distinguishability between the orientation of the shape and the orientation of the environment; (2) the distinguishability between adjacent angles; (3) the distinguishability between adjacent sides.

As we can see from the above figure, what subjects are doing is removing these three distinguishabilities, backwards in time as prescribed by the Asymmetry Principle. That is, successively, the orientation of the shape becomes the same as that of the environment, the sizes of the adjacent angles becomes the same, and the sizes of the adjacent sides become the same. To repeat: Asymmetries become symmetries backward in time - as predicted by the Asymmetry Principle.

Now let us use the Symmetry Principle. It says that the symmetries must be preserved, backward in time. Well, the rotated parallelogram has two symmetries: (1) opposite angles are indistinguishable in size; and (2) opposite sides are indistinguishable in length.

Observe that both of these symmetries are preserved backward in time - thus corroborating the Symmetry Principle.
Now, those of you who have seen my book, might say to me: "There seem to be 100's of rules in your book. How can you say that there are actually only two rules?" Well, the reason is that, as I said earlier, the term symmetry means indistinguishability under transformations: Reflectional symmetry is indistinguishability under reflectional transformations; rotational symmetry is indistinguishability under rotational transformations, and so on. Thus you obtain the different kinds of symmetry by instantiating the different kinds of transformations in the definition of symmetry. The different rules of the book are obtained by instantiating different transformations within the Asymmetry Principle and Symmetry Principle. Notice that it is by doing this instantiation process that you obtain the different sources of memory that can exist in an organization.

In the paper so far, I have given you only an intuitive sense of the instantiation process. What I want to do now is show you how it works, in depth. We are going to examine the extraction of memory from a particular asymmetry called curvature extrema. We will see later that curvature extrema are violations of rotational symmetry in the outline of a shape.

So lets look at curvature extrema. What is a curvature extremum? Well, first we note that curvature, for curves in the 2D plane, is simply the amount of bend. The straight line has no bend, and therefore has no curvature. As you successively increase bend, you are increasing curvature. Finally, observe that on a shape such as a finger, there is a point that has more bend than the other points on the line (the finger tip). This is a curvature extremum.

We will start be elaborating two successive rules by which the curvature extrema can be used to infer processes that have acted upon a shape. The input to the rules will be smooth outlines of shapes such as embryos, tumors, clouds, etc. So the rules will infer the history of such objects - that is, convert them into memory.

The inference, from curvature extrema to historical processes will be seen as requiring two stages: (1) Curvature extrema Symmetry axes, and (2) Symmetry axes Processes. We first consider stage 1.

NEXT PAGE