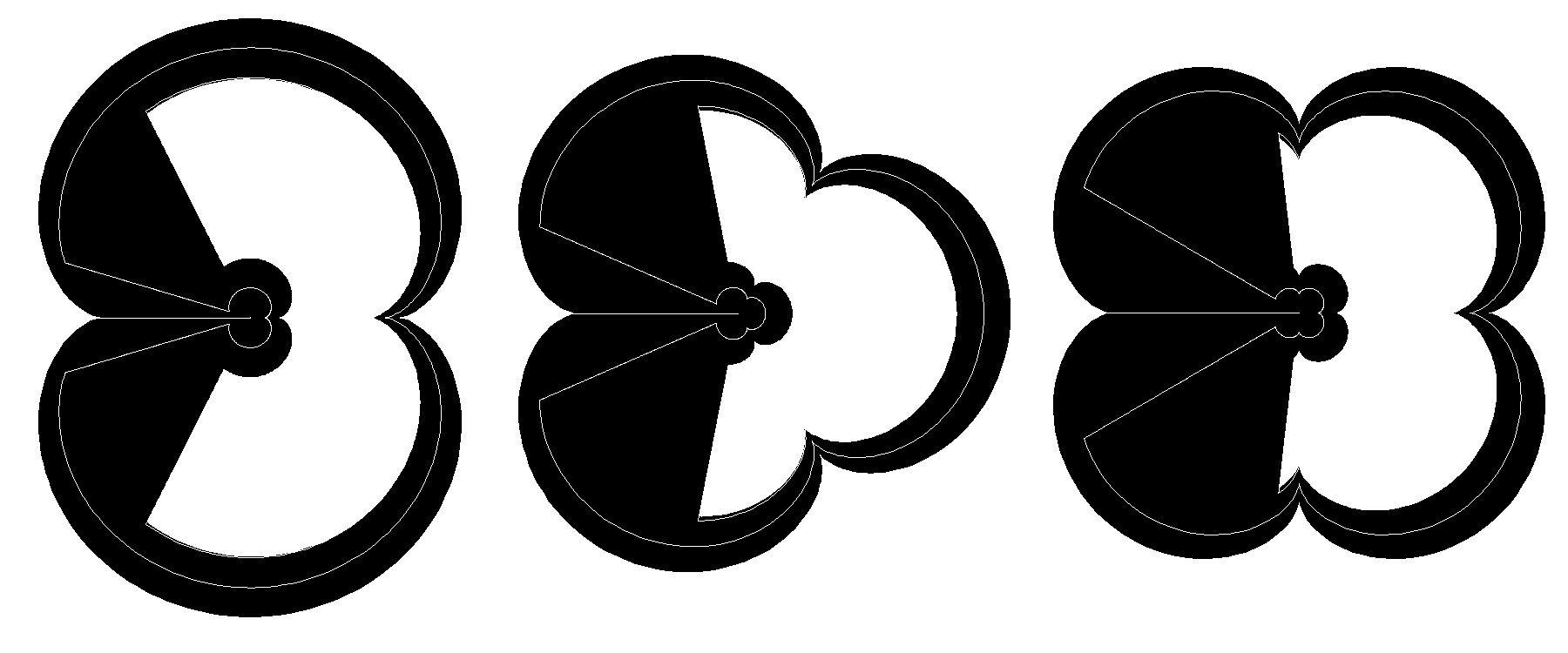|
More Curved Spirolaterals Robert J, Krawczyk College of Architecture Illinois Institute of Technology Chicago, IL 60616 USA E-mail: krawczyk@iit.edu
Abstract
1. Introduction A spirolateral is created by drawing a set of lines; the first at a unit length, then each additional line is increased by one unit length while turning to a constant angle. To complete a closed spirolateral, it is necessary to only repeat this procedure until the starting point is reached. The first apparent reference to this geometric figure was by Odds [8]. Further information can be found at Abelson [1] and Gardner [3]. In addition to the property of closure, spirolaterals need not always turn the same direction. The direction can be reversed at any turn, which makes the total number of possible spirolateral unknown. 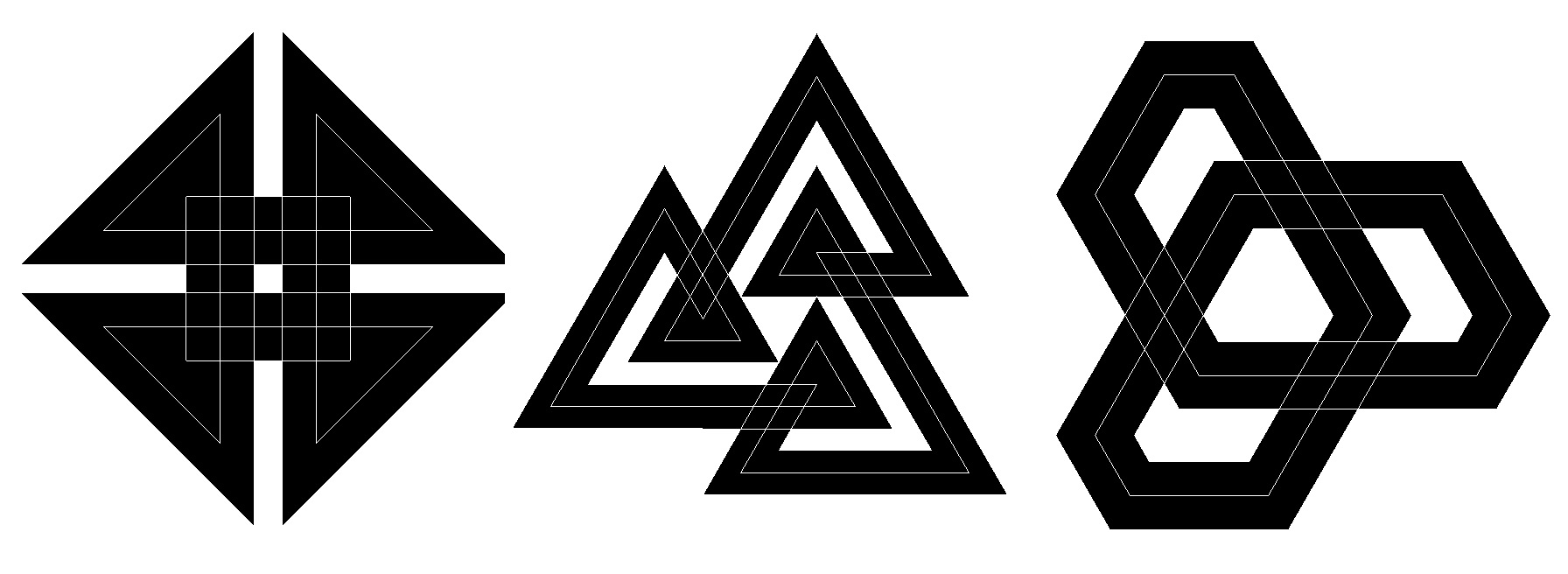
245 460 4120 Figure 1: Closed spirolaterals In this series of investigations, spirolaterals were generated to determine predictable closure and the variety of angles that could be used for turns as in Krawczyk [4]. The image of the spirolaterals remained as single lines. Reversals were the next area of interest. Krawczyk [6] covers the generation of all the unique reversals of any particular spirolateral. While developing software for the generation of spirolaterals as artwork, the single line was re-evaluated as the only representation. The turning line was given a thickness, and options were included to overlay a center line, edge lines, or corner lines. These options were included in Krawczyk [5], in the web site, www.netcom.com/~bitart, and in the Bridges 2001 Electronic Exhibition, which displays 200 spirolaterals. The web site also includes a JAVA program to generate your own variations. Figure 1 displays a sample of closed spirolaterals, and Figure 2 ones with reversed turns. The notation for identifying spirolaterals starts with
the number of turns, followed by the turning angle, then a list of the
reversed turns, if present.
5901,3,4,6,7 4601,3,43361,3 Figure 2: Closed spirolaterals with reversals 2. Curved Spirolaterals One of the extensions of using spirolaterals as artwork
beyond their original image was first discussed in Krawczyk [5].
A spirolateral consists of lines drawn between two vertices. Instead of
using the actual lines, one idea was to use only the vertices. Using CAD-based
software, procedures were written to interpret the vertices as control
points for curves. Figure 3 displays this concept. The
simple 190 spirolateral, a square, consists of four vertices.
These vertices can be fitted with arcs at the start and end of adjacent
vertices. The vertices can also be control points to generate a spline
curve.
Original Vertices Curve Fit Spline Figure 3: Curved spirolateral 190 Many of the spirolaterals developed as curves were found
to be interesting but not visually exciting nor did they generate any unexpected
images. The first set created were ones that consisted on ten or less turns.
Figure 4 displays one of these.
Figure 4: Curved spirolateral 790 Only when the number of turns increased to a range of
11 to 15, with reversed turns included, did the number of control points
increase to the point where they begin to generate images of unexpected
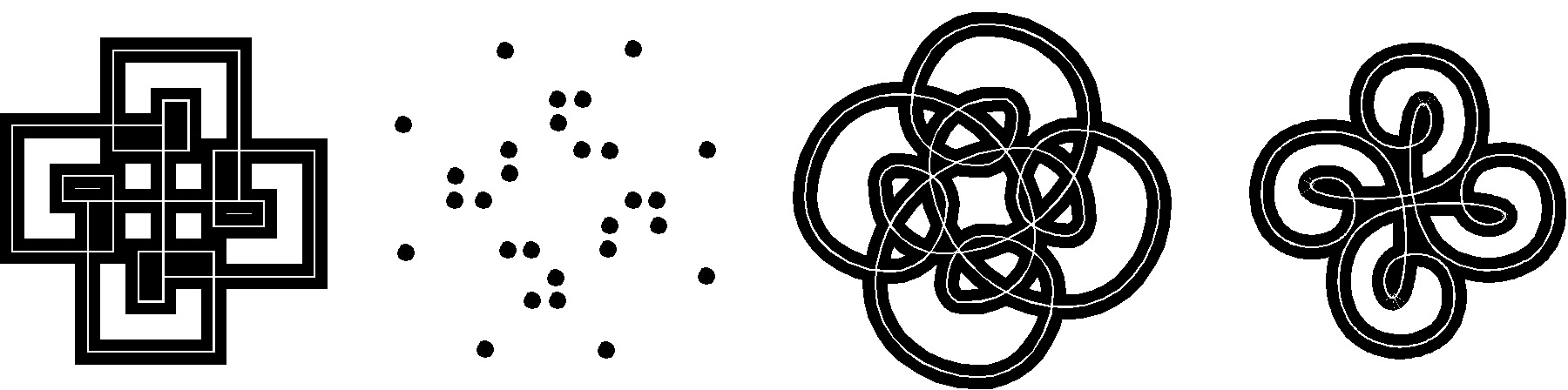
detail and complexity. Figure 5 displays two such examples.
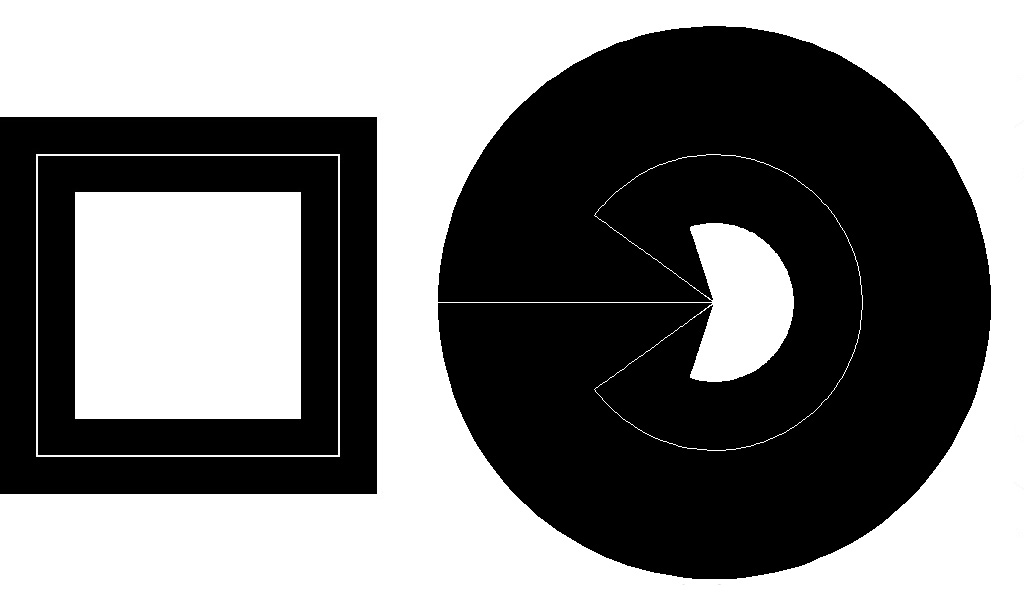
Figure 5: Curved spirolaterals of 1490 3. Curves by Inversion Another approach to curving spirolaterals is to apply a transformation, a projection, or mapping from a linear image to a curved one. In researching these possibilities, the first one encountered that was interesting was the concept of inversion, as described by Weisstein [9], Dixon [2] and Lawerence [7]. This mathematical method turns lines into circles. The transformation based on the image midpoint is as follows: X = (x * r2) / (x2 + y2) Y = (y * r2) / (x2 + y2) Figure 6 demonstrates this transformation on a simple square spirolateral. Inversion by definition reconstructs the spirolateral
as curves. After transforming a variety of spirolaterals, it was found
that ones that are open in the center generate the most interesting results.
Ones that have lines that cross the image midpoint generate very strange
results, which are visually not interesting. Symmetry also added to the
quality of the results, as did the selection of the line thickness. Figure
7 displays a sample of spirolateral inversions.
Figure 6: Inversion of spirolateral 190
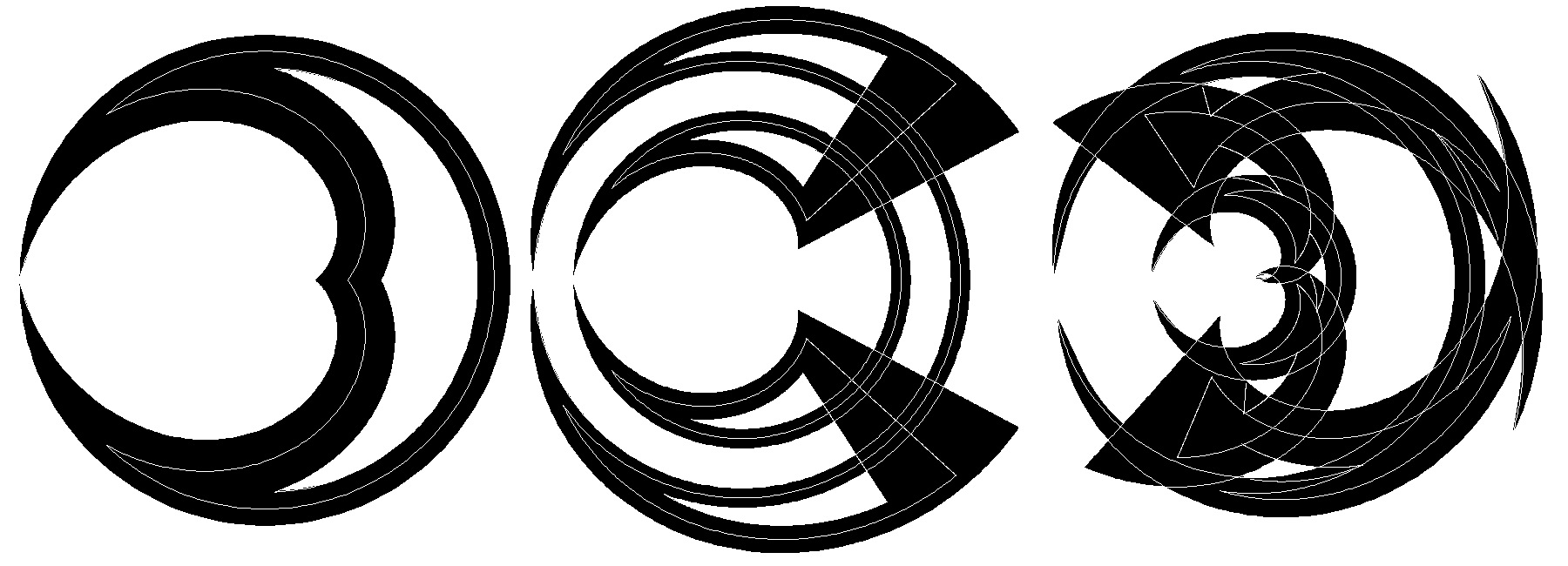
7901,3,4,6,7 245 230 Figure 7: Spirolateral inversions 4. Circular Transformations Continuing the search for other methods of curving spirolaterals, Dixon [2] in a section on transformations outlines a method he calls anitMercator. Horizontal lines become circles concentric with the coordinate origin, vertical lines become radial, and slanting lines become logarithmic spirals. The transformation in polar coordinates is as follows: A = k * x where: k = 2p /(xmax-xmin) R = exp(k * y) Figure 8 demonstrates this transformation on a simple square spirolateral. This transformation is affected by the line thickness and also by the offset from the origin. The origin is positioned in the lower-left corner of the image. This location results in the image being bent clockwise starting with the left corner. Figure 9 displays
a sample of spirolateral transformed by antiMercator.
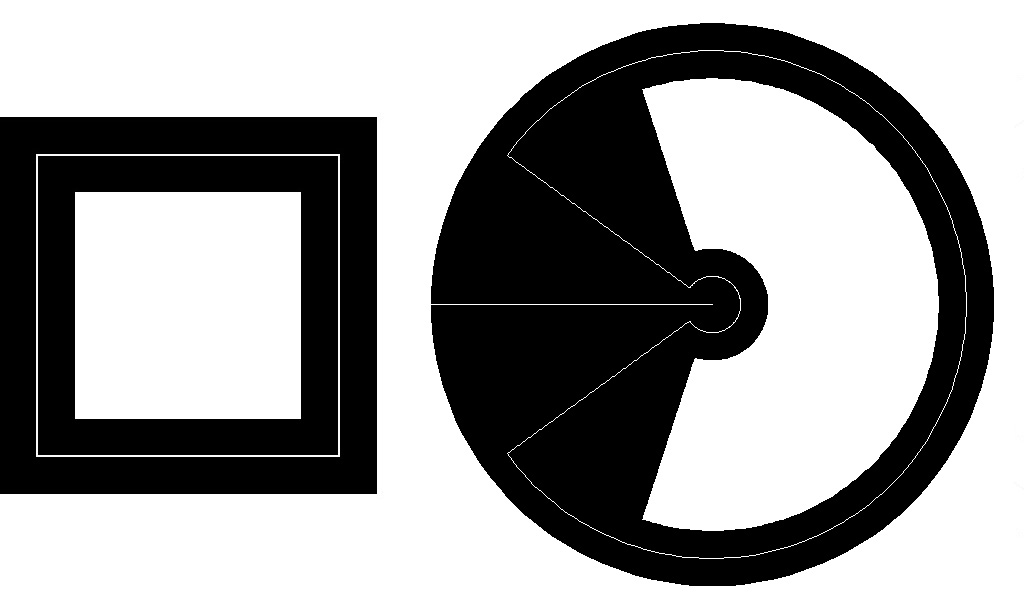
Figure 8: antiMercator spirolateral 190
160 230 390 Figure 9: antiMercator
spirolaterals While investigating the antiMercator transformation, one alternate method was found by removing the exponential function. The circular form remains without the logarithmic spiral effect. Since no formal name has been found for this transformation, it will be referred to as simply Circular. Figure 10 demonstrates this circular transformation on a simple square spirolateral. This transformation differs from the antiMercator in that
the line spacing is of a more constant distance from the center, so that
the original distances are better represented. This transformation also
changes as the offset increases. Figure 11 displaysa
sample of spirolateral transformed by the Circular transformation.
Figure 10: Circular spirolateral 190
160 245 230 Figure 11: Circular spirolaterals 5. Following a Curve The antiMercator and Circular transformation consist of computing polar coordinates based on the original image and then converting them to Cartesian coordinates. An alternate method is to not convert the polar to rectangular Cartesian coordinates but to follow curved ones. Using the angle and radius computation from the Circular transformation, the modified Cartesian coordinates are computed with the following curves, as in Lawerence [7]: Hypocycloid: X = R * (cos(A)*(n-1) + cos(A*(n-1))) where: n = number of cusps, 3 and 4 Y = R * (sin(A)*(n-1) - sin(A*(n-1))) Epicycloid: X = R * (cos(A)*(n+1) - cos(A*(n+1))) where: n = number of cusps, 2, 3, and 4 Y = R * (sin(A) (n+1) - sin(A*(n+1))) The major difference between these two curves is that the Hypocycloid produces concave curves and the Epicycloid produces convex ones. Figures 12 and 13
demonstrate these transformations on a simple square spirolateral.

Figure 12: Hypocycloid spirolateral 190
Figure 13: Epicycloid spirolateral 190 Figures 14 and 15
display sample of spirolaterals using the Hypocycloid and Epicycloid curves.
160 245 390 Figure 14: Hypocycloid spirolaterals
245 230 390 Figure 15: Epicycloid spirolaterals These transformations produce much more delicate curves due to the effect of the line thickness. The Hypocycloid is particularly interesting because of the very sharp point where its curves meet. It is also the transformation that produces concave curves. The Epicycloid is somewhat similar to the antiMercator and Circular transformation except for the unequal treatment of vertical and horizontal lines, as they generate a changing radius. Both generate quite a series of unexpected results.
As the mathematical basis of these forms evolves and image
variations are developed, there is a sense that even though it is at times
difficult to predict an outcome, the resulting images have a strange familiarity
to them, reminiscent of decorative patterns from the ancient world. On
the other hand the sharp edges, the lack of color, and the natural mathematical
presentation give them a distinctly futuristic look. It may be very difficult
to judge totally new forms since the aesthetic we use is based on all of
our previous visual experience and training. The potential for the unexpected
is clearly there, even from the simplest of beginnings.
References [1] Abelson, Harold, diSessa, Andera, Turtle Geometry, MIT Press, pp.37-39, 120-122, 1968. [2] Dixon, Robert, Mathographics, Dover Publications, Inc., p.152, 1987. [3] Gardner, Martin, Knotted Doughnuts and Other Mathematical Entertainments, W. H. Freemand and Company, pp. 205-208, 1986. [4] Krawczyk, Robert, "Spirolaterals, Complexity from Simplicity", in International Society of Arts, Mathematics and Architecture 1999, edited by N. Friedman and J. Barrallo, The University of the Basque Country, pp. 293-299, 1999. [5] Krawczyk, Robert, "The Art of Spirolaterals", in The Millennial Open Symposium on the Arts and Interdisciplinary Computing, edited by D. Salesin and C. Sequin, University of Washington, pp. 127-136, 2000. [6] Krawczyk, Robert, "The Art of Spirolateral Reversal", in International Society of Arts, Mathematics and Architecture 2000, edited by N. Friedman, University of Albany-SUNY, 2000. [7] Lawrence, J. Dennis, A Catalog of Special Curves, Dover Publications, Inc., p.43, 1972. [8] Odds, Frank, "Spirolaterals", Mathematics Teacher, February 1973, pp.121-124. [9] Weisstein, Eric, Concise
Encyclopedia of Mathematics, CD-ROM edition 1.0, Chapman &
Hall/CRCnetBASE, 1999.
|