: The Josephus Problem in : Recursive relations and some

An interesting fact about the Josephus Problem in Both Directions.

There is a very interesting fact about the function $JI(n)$.

Example 3.1   The list of the sequence $\{JI(n), n = 1,2,3,...,63 \}$is
$\{1, 1, 3, 4, 3, 6, 1, 3, 9, 1, 11, 5, 11, 7, 9, 14, 5, 12, 7, 12, 11,14, 9,......5, 43, 7, 41, 19, 33, 17, 35, 13, 43, 15, 41, 27, \\ 33, 25,35, 29, 35, 31\}.$
We denote this sequence $JI(n)$ modulo 2 by $JI(\ mod \ 2)$. Then $JI(\ mod \ 2)$ is
$\{1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0...... 1, 1, 1, 1, 1, 1, 1, 1,1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1\}.$
We can find a very beautiful pattern if we arrange them as the following.

$${\tiny \begin{array}{c} JI(1) \\ JI(2) JI(3) \\ JI(4) JI(5) JI(6)......2) JI(23) JI(24) JI(25) JI(26) JI(27) JI(28) JI(29) JI(30) JI(31) \end{array} }$$

(3.1)

$$\begin{array}{c} 1 \\ 1, 1 \\ 0, 1, 0, 1 \\ 1, 1, 1, 1, 1, 1, 1, 1\\ 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1 \end{array}$$

(3.2)

We are going to present a formula for this pattern in Theorem 3.2.

Lemma 3.1 (a)   $JI(2m+1)$ is odd number for any non-negative integer $m$.
(b) $JI(2m)$ is even if and only if $JI(2m) \geq m+1$ for any natural number $m$.

Proof (a)   By (2),(4),(6) and (8) of Theorem 2.1 we know that $JI(n)$ is odd number for any odd number $n$.
(b-1) Suppose that $2m = 8n$ for some natural number n. If $JI(8n)$ is even, then By (1) of Theorem 2.1 $\lfloor JI(2n)/(n+1) \rfloor$ =1,
which implies that $JI(2n) \geq n+1$. Then by (1) of Theorem 2.1 $JI(8n) \geq 4(n+1) -1 -1 \geq 4n + 1.$ Conversely if $JI(8n) \geq 4n + 1$, then by (1) of Theorem 2.1 we have $JI(2n) \geq n+1$. Then $\lfloor JI(2n)/(n+1) \rfloor$ =1 and by (1) of Theorem 2.1 we know that $JI(8n)$ is even. We have proved (b) for $2m = 8n$.
(b-2) Suppose that $2m = 8n+2$ for some natural number n. By the same method that we used in (b-1) we can prove that $JI(8n + 2)$ is even if and only if $JI(2n) \geq n + 2$. Similarly we have $JI(2n) \geq n + 2$ if and only if $JI(8n + 2) \geq 4n + 2$.
(b-3) Suppose that $2m = 8n+4$ for some natural number n. By the same method that we used in (b-1) we can prove that $JI(8n+4)$ is even if and only if $JI(2n+1) \leq n+1$. Similarly we can prove that
$JI(2n+1) \leq n+1$ if and only if $JI(8n+4) \geq 4n + 3$.
(b-4) Suppose that $2m = 8n+6$ for some natural number n. By the same method that we used in (b-1) we can prove that $JI(8n+6)$ is even if and only if $JI(2n+1) \leq n+1$. Similarly we can prove that
$JI(2n+1) \leq n+1$ if and only if $JI(8n+6) \geq 4n + 4.$

Our aim in this section is to prove the existence of the pattern in $(\ref{naitopattern})$. By Lemma 3.1 $JI(2m)$ is even if and only if $JI(2m) \geq m+1$, and hence it is important to know $JI(2m) \geq m+1$ or not for any natural number $m$.

Lemma 3.2   $[I]$ Suppose that $JI(2n) \leq n$ or $JI(2n) \geq n+1$, then
(a) $JI(8n) \leq 4n$ or $JI(8n) \geq 4n + 1$,
(b) $JI(8n+1) \geq 4n+2$ or $JI(8n+1) \leq 4n+1$,
(c) $JI(8n+2) \leq 4n+1$ or $JI(8n + 2) \geq 4n + 2$ and
(d) $JI(8n+3) \geq 4n+3$ or $JI(8n+3) \leq 4n+2$ respectively.
$[II]$ Suppose that $JI(2n+1) \leq n+1$ or $JI(2n+1) \geq n+2$, then
(e) $JI(8n+4) \geq 4n + 3$ or $JI(8n+4) \leq 4n+2$,
(f) $JI(8n+5) \leq 4n+3$ or $JI(8n+5) \geq 4n+4$,
(g) $JI(8n+6) \geq 4n+4$ or $JI(8n+6) \leq 4n+3$ and
(h) $JI(8n+7) \leq 4n+4$ or $JI(8n+7) \geq 4n+5$ respectively.

Proof   $[I]$ (a) First we suppose that

$$JI (2 n) \leq n .$$

(3.3)

By (1) of Theorem 2.1 $JI(8n) = 4JI(2n) - 1 - \lfloor JI(2n)/(n+1) \rfloor$, and hence by $(\ref{proofoflemmaforH1})$

$$JI(8n) = 4 JI(2 n) - 1.$$

(3.4)

By $(\ref{proofoflemmaforH1})$ and $(\ref{proofoflemmaforH2})$ we have $JI(8n) \leq 4n - 1 \leq 4n$.
Next we suppose that

$$JI (2 n) \geq n+1 .$$

(3.5)

By Theorem 2.1 and $(\ref{proofoflemmaforH3})$

$$JI(8n) = 4 JI(2 n) - 2.$$

(3.6)

By $(\ref{proofoflemmaforH3})$ and $(\ref{proofoflemmaforH4})$ we have $JI(8n) \geq 4(n+1) - 2 \geq 4n+1$.
Therefore we have proved (a) of this theorem.
By the similar method we are going to prove (b), (c) and (d).
Suppose that $JI(2n) \leq n$ or $JI(2n) \geq n+1$. Then by Lemma 2.1 $JI(2n) \neq n + 1$, and hence we have $JI(2n) \leq n$ or $JI(2n) \geq n + 2$.
(b) By (2) of Theorem 2.1 we have $JI(8 n + 1) \geq 8n + 5 - 4n = 4n + 5$ or $JI(8 n + 1) \leq 8n+5-4(n+1) = 4n + 1$ respectively. Therefore we have proved (b).
(c) By (3) of Theorem 2.1 we have $JI(8 n + 2) \leq 4n - 3 \leq 4n+1$ or $JI(8 n + 2) \geq 4(n+2) - 4 = 4n + 4 \geq 4n+2$ respectively.
We have proved (c).
(d) By (4) of Theorem 2.1 we have
$JI(8 n + 3) \geq 8n + 7 - 4n = 4n + 7 \geq 4n+3$ or $JI(8 n + 3) \leq 8n + 7 - 4(n +2) = 4n - 1 \leq 4n+2$ respectively. We have proved (d).
$[II]$ Next we are going to prove (e),(f),(g) and (h). Suppose that $JI(2n+1) \leq n+1$ or $JI(2n+1) \geq n+2$.
(e) By (5) of Theorem 2.1 we have $JI(8 n + 4) \geq 8n + 8 - 4(n + 1) = 4n + 4 \geq 4n+3$ or $JI(8 n + 4) \leq 8n + 8 - 4(n + 2) + 1= 4n + 1 \leq 4n + 2$ respectively.
We have proved (e).
(f) By (6) of Theorem 2.1 we have $JI(8 n + 5) \leq 4(n + 1) - 1 = 4n + 3$ or $JI(8 n + 5) \geq 4(n + 2) - 1 = 4n +7 \geq 4n + 4$ respectively.
We have proved (f).
(g) By (7) of Theorem 2.1 we have $JI(8 n + 6) \geq 8n + 10 - 4(n+1) = 4n + 6 \geq 4n + 4$ or $JI(8 n + 6) \leq 8n + 10 - 4(n+2) + 1 = 4n + 3$ respectively.
We have proved (g).
(h) By (8) of Theorem 2.1 we have $JI(8 n + 7) \leq 4(n + 1) -3 = 4n + 1 \leq 4n + 4$ or $JI(8 n + 7) \geq 4(n + 2) -3 = 4n + 5$ respectively.
We have proved (h).

Definition 3.1   To use Lemma 3.2 we need a function. We define $H(n)$ by

$H(2n)= \begin{cases}0 & ( \text{ if } JI(2n) \leq n ) \\1 & ( \text{ if }JI(2n) \geq n+1 )\\\end{cases}$
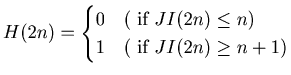
for any natural number $n$ and
$H(2n+1)= \begin{cases}0 & ( \text{ if } JI(2n+1) \leq n+1 ) \\1 & ( \text{ if }JI(2n+1) \geq n+2 )\\\end{cases}$
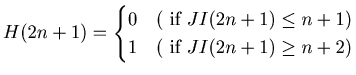
for any non-negative integer $n$.

In short $H(n)$ = 0 or 1 if $JI(n)$ is in the first or the second half of the list $\{1,2,...,n \}$. $H(n)$ is a useful function when we study the pattern in $(\ref{naitopattern})$.

Lemma 3.3   Let $m$ be a natural number. (1) $JI(2m+1) = 1$ $(mod \ 2)$. (2) $JI(2m) = 0$ $(mod \ 2)$ if and only if $H(2m) = 1.$

Proof   This is direct from Definition 3.1 and Lemma 3.1.

This function $H(n)$ has simple recursive relations.

Lemma 3.4   Suppose that $H(2n) = 0$ or $1$, then
(1) $H(8n) = 0$ or $1$,
(2) $H(8n+1) = 1$ or 0,
(3) $H(8n+2) = 0$ or $1$ and
(4) $H(8n+3) = 1$ or $0$ respectively.
Suppose that $H(2n+1) = 0$ or $1$, then
(5) $H(8n+4) = 1$ or 0,
(6) $H(8n+5) = 0$ or $1$,
(7) $H(8n+6) = 1$ or 0 and
(8) $H(8n+7) = 0$ or $1$ respectively.

Proof   This is direct from Theorem 3.2 and Definition 3.1.

Example 3.2   The sequence {H(n), n = 1,2,... } has a very beautiful pattern. First we make a triangle with H(n) for n = 1,2,3,..,31.

$${\tiny \begin{array}{c} H(1) \\ H(2) H(3) \\ H(4) H(5) H(6) H(7) ......H(21) H(22) H(23) H(24) H(25) H(26) H(27) H(28) H(29) H(30) H(31) \end{array} }$$

(3.7)

We are going to calculate each H(n) using Definition 3.1 and Lemma 3.4.
Since JI(1)=1, JI(2)=1, JI(3) = 3, by Definition 3.1 we have H(1) = 0, H(2) = 0, H(3) = 1.
Since H(1) = 0, let n = 0 and by using (5), (6), (7) and (8) of Lemma 3.4 we have {H(4), H(5), H(6), H(7)} = {1,0,1,0}.
Since H(2) = 0 and H(3) = 1, let n = 1 and by using (1), ..., (8) of Lemma 3.4 we have
{H(8),H(9),H(10),H(11),H(12),H(13),H(14),H(15)} = {0,1,0,1,0,1,0,1}.
Since H(4) = 1 and H(5) = 0, let n = 2 and by using (1), ..., (8) of Lemma 3.4 we have {H(16),H(17),H(18),H(19),H(20),H(21),H(22),H(23)} = {1,0,1,0,1,0,1,0}. Since H(6) = 1 and H(7) = 0, let n = 3 and by using (1), ..., (8) of Lemma 3.4 we have
{H(24),H(25),H(26),H(27),H(28),H(29),H(30),H(31)} = {1,0,1,0,1,0,1,0}.
Therefore we can calculate the value of each H(n) in 3.7, and we get the following triangle of numbers.

$$\begin{array}{c} 0 \\ 0, 1 \\ 1, 0, 1, 0 \\ 0, 1, 0, 1, 0, 1,......1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1\\ \end{array}$$

(3.8)

We can make a theorem by generalizing the pattern we found in Example 3.2.

Theorem 3.1 (1)   Suppose that $2^{2s} \leq m \leq 2^{2s+1}-1,$ then
$H(m)= \begin{cases}1 & ( \text{ if m is an even number} ) \\0 & ( \text{ if m is an odd number} ).\\\end{cases}$
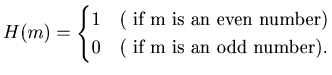
(2) Suppose that $2^{2s+1} \leq m \leq 2^{2s+2}-1,$ then
$H(m)= \begin{cases}0 & ( \text{ if m is an even number} ) \\1 & ( \text{ if m is an odd number} ).\\\end{cases}$

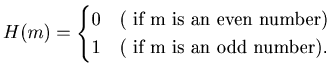
Proof   Here we can use the method that is similar to the one used in Example 3.2. By Lemma 3.4 we can get the values of H(8n), H(8n+1), H(8n+2), H(8n+3), H(8n+4),H(8n+5), H(8n+6),H(8n+7) from the values of H(2n) and H(2n+1) for any natural number $n$. In this way we can prove this theorem.

Example 3.3   Now we are going to show how the pattern in $(\ref{Hrelation2})$ and Lemma 3.3 produce the pattern in $(\ref{naitopattern})$.
By Lemma 3.3 $JI(2m+1)$ is odd for any non-negative number $m$.
By $(\ref{Hrelation})$ and $(\ref{Hrelation2})$ we have
{H(2),H(4),H(6),H(8),H(10),H(12),H(14),H(16),H(18)}
= {0,1,1,0,0,0,0,1,1}, and hence by Lemma 3.3 we have
{JI(2),JI(4),JI(6),JI(8),JI(10),JI(12),JI(14),JI(16),JI(18) }
= {1,0,0,1,1,1,1,0,0}.
In this way we can calculate
$JI(20), JI(22), ...,JI(30)$ by $H(20), H(22),...,H(30)$.

Theorem 3.2 (1)   Suppose that $2^{2s} \leq m \leq 2^{2s+1}-1,$ then
$JI(m)= \begin{cases}0 & ( \text{ mod 2 if m is an even number} ) \\1 & ( \text{ mod 2 if m is an odd number} ),\\\end{cases}$
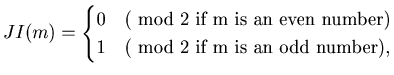
(2) Suppose that $2^{2s+1} \leq m \leq 2^{2s+2}-1,$ then
$JI(m) = 1$ $(mod \ 2)$.

Proof   We can prove this theorem by the same method that we used in Example 3.3. By Lemma 3.3 $JI(2m+1)$ is odd for any non-negative integer $m$.
By Theorem 3.1 and Lemma 3.3 we can get the values of $JI(2m)$ for any natural number $m$.

Example 3.4   Figure (3.1) is the graph of the list {JI(n) , $n = 2$, 3, ..., 256} and Figure (3.2) is the graph of the list {JI(n) , $n = 2$, 3, ..., 1024}. The horizontal coordinate is for the number of numbers (or people in the original Josephus problem) involved in the game, and the vertical coordinate is the number that remains when the game is over. For example by $JI(256) = 214$ we have the point $(256, 214)$ in the graph.
.

Figure (3.1.) 　　　　　　　　　　　　　　　　　　Figure (3.2)
If we compare Figure 3.1 and 3.2, we can discover a very interesting fact. That is the existence of self-similarity. As to the research of self-similarity by the authors see $\cite{suurikaiseki}$.

Is there any relation between the patterns of the sequence {$JI(n)$, n = 1,2,...} and the self-similarity of Figure (3.1) and Figure (3.2)?

Example 3.5   Here we present recursive relations that have nothing to do with the Josephus problem. First we let $F(1) = F(2) = 1$, $F(3) = 3$ and $F(4) = 4.$
(1) $F(8n) = 4F(2n) - 1 - 2\lfloor F(2n)/(n+1) \rfloor$.
(2) $F(8n+1) = 8n+5-4F(2n).$
(3) $F(8n+2) = 4F(2n)-3-2 \lfloor F(2 n)/(n + 2) \rfloor$
(4) $F(8n+3) = 8n+7-4F(2n).$
(5) $F(8n+4) = 8n+9-4F(2n+1)+ 2\lfloor F(2n+1)/(n+2) \rfloor.$
(6) $F(8n+5) = 4F(2n+1)-1.$
(7) $F(8n+6) = 8n+11-4F(2n+1)+ 2\lfloor F(2n+1)/(n+2)\rfloor.$
(8) $F(8n+7) = 4F(2n+1)-3.$
If we calculate $F(m)$ for $m = 1,2,...,63,$ we get {1, 1, 3, 4, 3, 7, 1, 3, 9, 1, 11, 7, 11, 9, 9, 13, 5, 11, 7, 13, 11, 15, 9, 25, 1, 23, 3, 29, 3, 31, 1, 11, 25, 9, 27, 7, 35, 9, 33, 3, 41, 1, 43, 7, 43, 9, 41, 25, 25, 25, 27, 15, 43, 17, 41, 33, 25, 31, 27, 31, 35, 33, 33}. In these numbers 4 is the only even number. In fact this is the only even number in {$F(m)$, $m = 1,2,...,200000$} by the calculation of the computer algebra system Mathematica.
Figure (3.3) is the graph of the list {F(n) , $n = 2$, 3, ..., 256} and Figure (3.4) is the graph of the list {F(n), $n = 2$, 3, ..., 1024}.

Figure (3.3.) 　　　　　　　　　　　　　　　　　Figure (3.4)
The sequence {F(n) $(mod \ 2)$, n = 1,2,...} = {1,1,1,0,1,1,1,...} does not have any interesting pattern, but the graph of it has the self-similarity. By this example we know that a sequence can produce a graph with the self-similarity even if it does not have any interesting pattern when reduced by 2. Therefore the authors think it is almost sure that there is not any relation between the pattern of sequence in 3.2 and the graph that is produced by it.

Acknowledgments
Contributions from Hiroshi Matsui, Soh Tatsumi and Takahumi Inoue. Although they were not the primary authors, their contributions were significant. We would like to thank Mr. Harrison Gray for helping us to prepare this article.

: The Josephus Problem in : Recursive relations and some