Formalization of enharmonic modulations

 

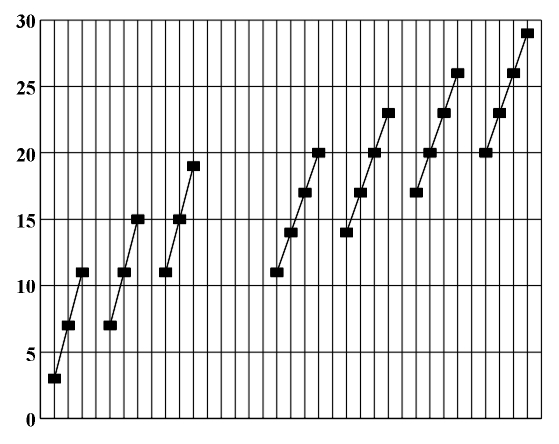
Each chord type is determined by a corresponding interval sequence. For example, a major triad is determined by the interval sequence of (4,3), an augmented triad is determined by the interval sequence of (4,4), a diminished seventh-chord by the sequence (3,3,3), a seventh chord with a diminished third and a doubly diminished fifth by the interval sequence of (2,3,4), etc. In the same manner, all chord inversions can be described by corresponding interval sequences. For example, in the case of the major triad (4,3), the first inversion is (3,5) and the second is (5,4). The first and second inversion of the augmented triad (4,4) are determined by an identical interval sequence (4,4). In general, for the triad (i₁,i₂) the first inversion is (i₂,12-i₁-i₂), and for the second inversion it is (i₂,12-i₁-i₂). All three inversions of the diminished seventh-chord (3,3,3) are also determined by the same interval sequence (3,3,3). For the first inversion of a seventh-chord with a diminished third and a doubly diminished fifth, the corresponding interval sequence is (3,4,3), for its second inversion the corresponding interval sequence is (4,3,2), and for the third inversion it is (3,2,3). In a general case, for the first inversion of seventh-chord (i₁,i₂,i₃) the corresponding interval sequence is (i₂,i₃,12-i₁-i₂-i₃), for the second inversion it is (i₃,12-i₁-i₂-i₃,i₁), and for the third inversion it is (12-i₁-i₂-i₃,i₁,i₂).

In the process of constructing a chord inversion, it may occur that the obtained interval sequence also corresponds to a chord in its basic position. This is not the case with the major triad, but is true of all the other given examples. All inversions of the augmented triad are augmented triads and all inversions of diminished seventh-chords are diminished seventh-chords (Fig. 6.2).

 

 

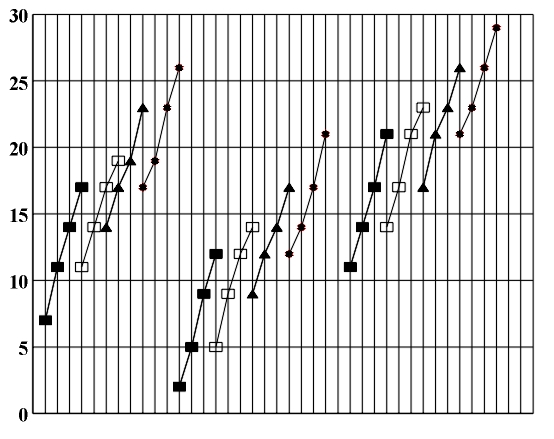
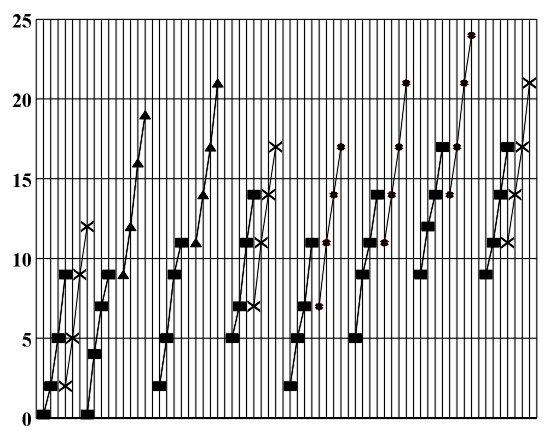
The interval sequence (3,4,3) of the first inversion of the seventh chord with a diminished third and a doubly diminished fifth (2,3,4) corresponds to the minor seventh-chord, the interval sequence of its second inversion (4,3,2) corresponds to the diminished seventh-chord and the interval sequence of its third inversion (3,2,3) corresponds to the chromatic seventh-chord which consists of a minor third, a diminished third and a minor third. The described transformation of one chord into a chord of the same or different type by means of inversions, allows for the possibility of changing the basic tone. The possibility of pronouncing some other tone as the basic tone based on these transformations is the basis of enharmonic modulation. For example, since the basic position and all the inversions of the augmented triad or diminished seventh-chord are identical in regards to interval sequences, every tone pertaining to them can be taken as the basic tone and thus all the prerequisites for enharmonic modulations are met. We can also, with the same purpose, pronounce the second tone of a seventh-chord with a diminished third and a doubly diminished fifth (2,3,4) as the basic tone, i.e. we can pronounce its first inversion (3,4,3) as a minor seventh-chord, etc.

We can deduce from the previous examples that only some chords can be used as the basis of enharmonic modulation. Since all diatonic and chromatic chords consist of intervals i=2,3,4 (diminished, minor and major thirds), based on the interval sequences that correspond to the chord inversions we may draw the following conclusion: in order for a chord to be transformed into a basic-position chord by inversion, the new intervals 12-i₁-i₂ (occurring in the triad inversion), and 12-i₁-i₂-i₃ (occurring in the seventh-chord inversion), must also be thirds (i.e., 2 £ 12-i₁-i₂ £ 4, and 2 £ 12-i₁-i₂-i₃ £ 4). For instance the major triad (4,3) does not meet this prerequisite, as 12-i₁-i₂=12-4-3=5. The augmented triad (4,4), the diminished seventh-chord (3,3,3) and the seventh-chord with a diminished third and a doubly diminished fifth (2,3,4) do meet it, since 12-i₁-i₂=12-4-4=4, 12-i₁-i₂-i₃=3, and 12-i₁-i₂-i₃=12-2-3-4=3, respectively.

In verifying the validity of the mentioned prerequisite in reference to all studied chords we may conclude that this prerequisite is met by the augmented triad (4,4) for which 12-i₁-i₂=4, the dominant seventh-chord (4,3,3), the minor seventh-chord (3,4,3), the half dimnished seventh-chord for which 12-i₁-i₂-i₃=2 (Fig. 6.3), the diminished seventh-chord (3,3,3) for which 12-i₁-i₂-i₃=3 and all chromatic seventh-chords (4,4,2), (4,2,4), (2,4,4) for which 12-i₁-i₂-i₃=2, (4,3,2), (4,2,3), (3 ,4,2), (3,2,4), (2,4,3) and (2,3,4) for which 12-i₁-i₂-i₃=3 and (3,3,2), (3,2,3), (2,3,3) for which 12-i₁-i₂-i₃=4.

All inversions of the given chords will also be chords in the basic position, except for the first inversion (4,2,2) and the second inversion (2,2,4) of the chromatic seventh-chord (4,4,2), the first and the third inversion (2,4,2) of the chromatic seventh-chord (4,2,4), and the third inversion (2,4,2) of the chromatic seventh-chord (2,4,4) which do not represent chords in the basic position (Fig. 6.4). At the same time, the augmented triad and the diminished seventh-chord are invariant in regards to inversions, i.e., they are transformed into same-type chords. The rest of the diatonic seventh-chords are transformed into chromatic chords, and the chromatic chords either into chromatic or diatonic.

Since with every modulation there is a tendency towards the stabilization of the newly-established tonality by way of cadence, special significance is given to the possibility of pronouncing an adequate inversion of a chord as the diatonic chord. An overview of such possibilities is given in the following table. In this table we will give

1) the initial chromatic chord;

2) the ordinal number of the inversion;

3) the inversion itself, representing a diatonic chord;

4) the type of the diatonic chord.

 

1)	2)	3)	4)
(4,3,2)	3	(3,4,3)	min/min
(4,2,3)	2	(3,3,4)	dim/min
(3,4,2)	3	(3,3,4)	dim/min
(3,2,4)	2	(4,3,3)	dom
(2,4,3)	1	(4,3,3)	dom
(2,3,4)	1	(3,4,3)	min/min
(3,3,2)	3	(4,3,3)	dom
(3,2,3)	2	(3,4,3)	min/min
(2,3,3)	1	(3,3,4)	dim/min

Figure 6.3. Diatonic seventh-chords and their inversions representing chromatic seventh-chords.

 

Figure 6.4. Inversions of chromatic seventh-chords representing diatonic seventh-chords.

Without going deeper into a detailed analysis of all the harmonic possibilities, the very type of thus obtained diatonic chords and their harmonic functions (dom as V (D) of major, harmonic major, and melodic major, and IV (S) of melodic major; min/min as V (D) of natural minor and IV (S) of natural minor and harmonic minor; dim/min as VII of major, II of natural and harmonic major and VI and VII of melodic major), testify as to the significance of chromatic chords as the basis of enharmonic modulations.

All the possibilities that occur in the case of enharmonic modulations can be directly identified in the tables of the versatility of triads, seventh-chords  and chromatic seventh-chords. By applying these tables it is possible to construct complete tables of all enharmonic modulations, analogous to the tables of diatonic modulations. Because of the vast number of possibilities that occur thanks to the versatility of chromatic seventh-chords, we will show only a part of the table of all major ® major enharmonic modulations. Only those enharmonic modulations in which the inversion of a chromatic seventh-chord is treated as the diatonic seventh-chord will be shown. In this table the following data are given:

1) the interval, made by the starting tones of the initial and final tonality;

2) the type of chromatic chord;

3) the degree where it is positioned in the initial tonality;

4) the ordinal number of the tone which we will pronounce as the basic tone;

5) the type of chord;

6) the degree where it is positioned in the final tonality.

 

1)	2)	3)	4)	5)	6)
i=2	1 (2,3,4)	II	2	min/min	II
i=2	2 (4,3,2)	V	4	min/min	II
i=2	7 (3,2,3)	VII	3	min/min	II
i=5	1 (2,3,4)	I	2	min/min	VI
i=5	1 (2,3,4)	V	2	min/min	III
i=5	2 (4,3,2)	I	4	min/min	III
i=5	2 (4,3,2)	IV	4	min/min	VI
i=5	7 (3,2,3)	VI	3	min/min	VI
i=7	1 (2,3,4)	II	2	min/min	VI
i=7	1 (2,3,4)	V	2	min/min	II
i=7	2 (4,3,2)	I	4	min/min	II
i=7	2 (4,3,2)	V	4	min/min	VI
i=7	7 (3,2,3)	VII	3	min/min	VI
i=10	1 (2,3,4)	I	2	min/min	III
i=10	2 (4,3,2)	IV	4	min/min	III
i=10	7 (3,2,3)	VI	3	min/min	III

Since any tone of the augmented fifth-chord may be pronounced as basic, it allows us to carry out the following enharmonic modulations: harmonic minor to harmonic minor, melodic minor to melodic minor, harmonic minor to melodic minor and vice versa. In the course of these modulations the initial and final tonalities build the interval i=4,8. In a similar manner, since any tone of the diminished seventh-chord may be pronounced as the basic tone, the diminished seventh-chord allows various enharmonic modulations thanks to its versatility.