Symmetry of fifth-chord coefficients of stability

 

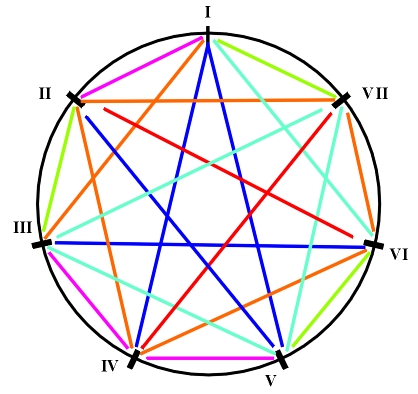
The instability of a fifth-chord can be measured according to its similarity with the tritone triangle (Despi\' c, 1987). Based on this, we define the coefficient of instability n of a fifth-chord as the number of common tones it shares with a tritone triangle (i.e., as a coefficient of similarity of a fifth-chord in regard to tritone triangle). Vice versa, the coefficient of stability of a fifth-chord can be expressed by the formula s=3-n ¹.

Thus the stability coefficient of the tonic fifth-chord is 3, for the subdominant it is 2, and for a dominant it is 1. Consequently, the harmonic crescendo in the case of a major key has the form T-S-D and in the case of a minor key, the tritone occurs on the II degree, whose secondary function is s (s-tritone), which produces a harmonic crescendo T-D-S.

The corresponding stability coefficient s can be found for any fifth-chord on any degree. For example, in the case of a major key, s(\textII)=1, as the fifth-chord which has 2 common tones with a tritone triangle is on the II degree (its instability coefficient is n=2, so s=1). In this manner we get the following table of stability coefficients s of the fifth chords that are positioned on different degrees of the major and minor key.

	major	minor
	s	s
I	3	3
II	1	0
III	2	3
IV	2	1
V	1	2
VI	3	2
VIII	0	1

The most stable fifth-chords are positioned on the I and VI degree of the major key, or on the III and I degree of the minor key. The obtained result offers an additional element for the study of the causes for the separation of natural major and natural minor from other modal scales - the action of the principle of stability: we have chosen the points of maximum fifth-chord stability (the I and VI degree of the major key and the III and I degree of the minor key) as the initial points of tone sequences. At the same time this means that the tonic function of the VI degree of the major key will be significantly stronger than its subdominant function, whereas the tonic function of the III degree of the natural minor will be more significant than its dominant function.

By using an analogous procedure it is possible to study the seventh-chord structure of natural scales. Of course, the transition to seventh-chords will not have any impact on harmonic functions. The table of the stability coefficient S=4-N of the seventh-chords is as follows:

 

	major	minor
	S	S
I	3	3
II	2	1
III	2	3
IV	3	2
V	1	2
VI	3	3
VIII	1	1

The sequence of the interval, fifth-chord, seventh-chord, and other structures in this study is descending in terms of symmetry and clearly illustrates the universal principle according to which symmetry decreases with the increment of the degree of structural organization.

Besides d-tritone on the VII degree, s-tritone appears on the II degree in the harmonic minor (Fig. 5.4)

 

(a)

(b)

Figure 5.4 A diagram of the interval structure of the harmonic minor (a) and melodic minor (b).

In the case of harmonic minor, by using the proposed procedure we get a diagram of the symmetry of interval structure. In this diagram an identification of complementary intervals has been made, i.e., the principle of minimal same-name intervals has been applied. In this diagram we can directly read the fifth-chord structure of the harmonic minor. The appearance of the tritone rectangle II-IV-VI-VII is evident at first sight. The instability of the fifth-chord on certain degrees is expressible in terms of their similarity with the tritone rectangle. As a result we get the following table of the stability coefficients of the fifth-chords:

	s
I	3
II	0
III	2
IV	1
V	1
VI	2
VIII	0

In this table we note the complete stability of the tonic fifth-chord and the uniformity of the kinetic role of the subdominant and dominant function. As for the stability of the fifth-chord, the function of the VI degree is equally close to the tonic and subdominant function. However, the distinctive stability of the seventh-chord on the VI degree (S=3) prevails in favor of the tonic function. The stability coefficients of seventh-chord S are as follows:

	S
I	3
II	1
III	2
IV	2
V	1
VI	3
VIII	0

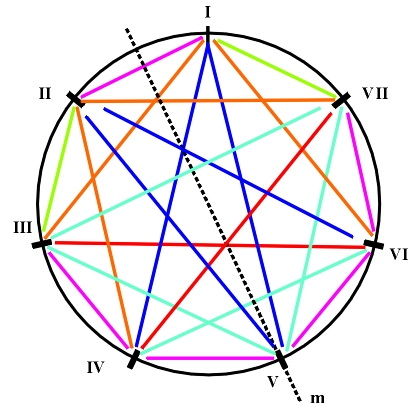
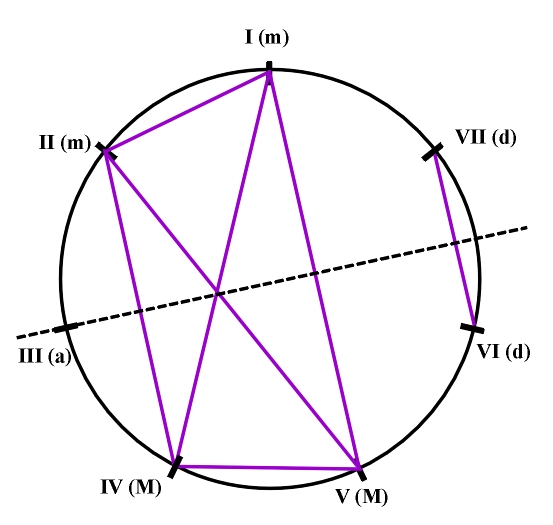
Based on this table we can deduce that the harmonic crescendo in the case of the harmonic minor will have the form T-S-D.

As opposed to the asymmetric interval structure of the harmonic minor (Fig. 5.4.a), the melodic minor has a symmetric interval structure (Fig. 5.4.b). There appears the axis of symmetry which contains the V degree and passes between the I and II degree. In regards to the symmetry of the fifth-chord structure, in the melodic minor the ambivalent symmetric function of the III degree stands out. Both the axis of symmetry for the VI and VII degree (dim-dim) and the axis of antisymmetry for the V and I, and the IV and II degree (maj-min) cross it simultaneously (Fig. 5.5).

In the melodic minor the d-tritone on the VII degree represents a source of instability. The t-tritone in the diminished fifth-chord on the VI degree has an inferior role, so that when calculating the coefficient of stability it occurs only as a correctional factor on the VI degree. Accordingly, the coefficients of stability of fifth-chords s and the coefficients of stability of the seventh-chords S have the following values:

	s	S
I	3	3
II	1	2
III	2	2
IV	2	3
V	1	1
VI	2	3
VIII	0	1

Based on this, the form of the harmonic crescendo is T-S-D.

 

Figure 5.5 The ambivalent symmetry function of the III degree of the melodic minor.

---

¹For the tritone fifth-chord n equals 3. Consequently, its stability coefficient is s=0.