|
Isometric transformations of melodic structure
The isometry transformations of a unison melodic structure are made up of the following kinds of transformations:
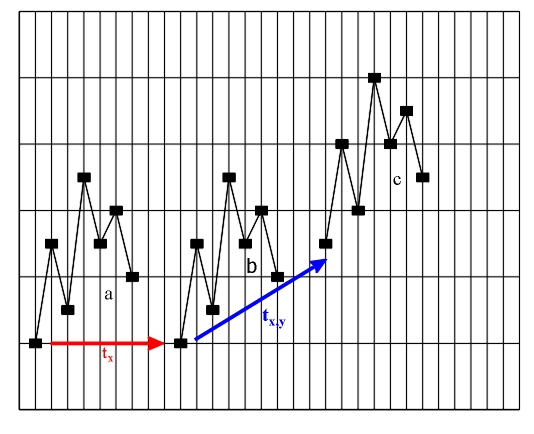
Figure 3.15 a)-b) Translational repetition (translation tx); b)-c) transposition (translation tx,y).
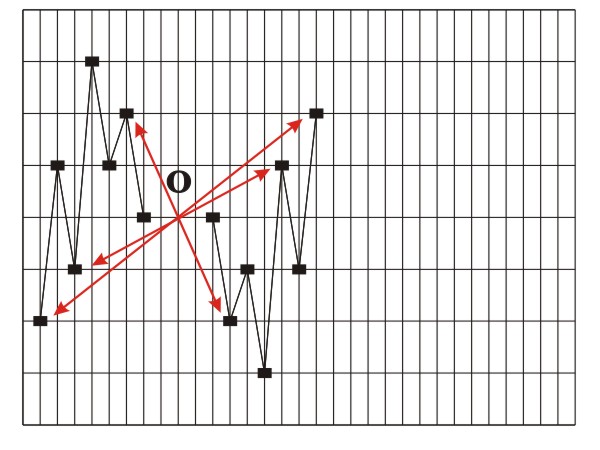
Figure 3.16 Retrograde inversion (central reflection O).
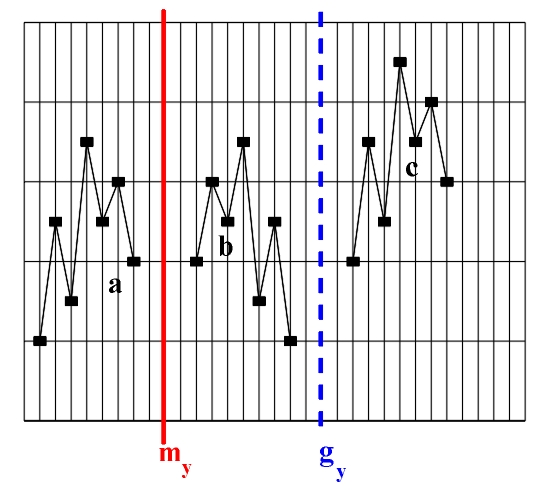
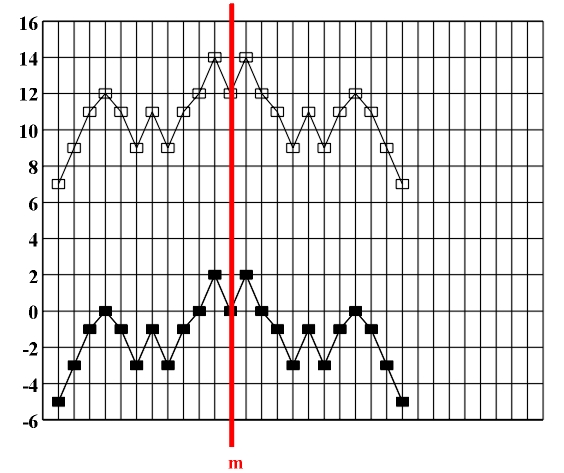
Figure 3.17 a)-b) Retrograde repetition (mirror reflection my); b)-c) retrograde transposition (glide reflection gy).
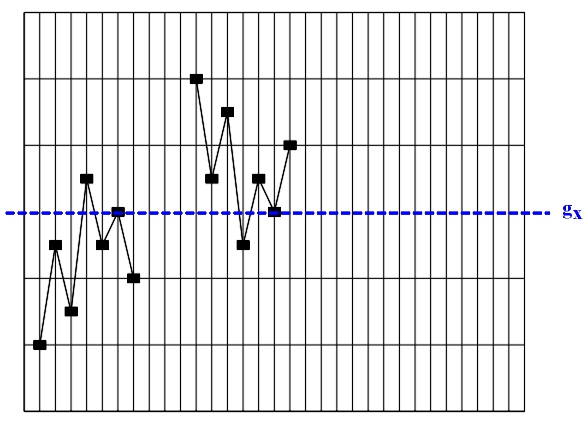
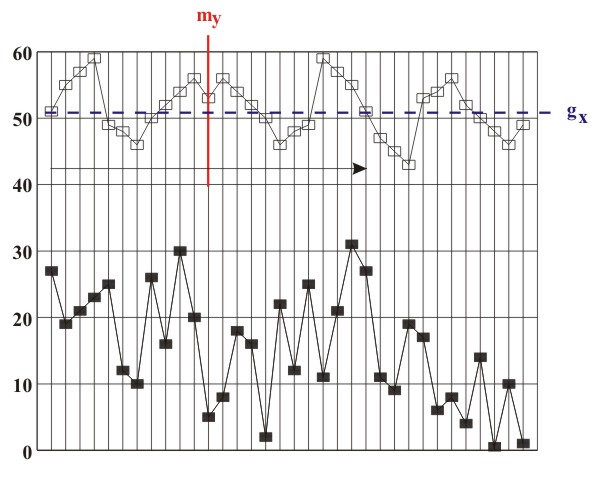
Figure 3.18 Inversion (glide reflection gx) Transposition (translation) and retrograde inversion (central reflection) are direct isometric transformations - orientation-preserving transformations. This means that by undergoing transposition and retrograde inversion, ascending intervals are transformed into ascending ones, and descending intervals are transformed into descending ones. Retrograde repetition (mirror reflection my), retrograde transposition (glide reflection gy) and inversion (glide reflection gx) are all indirect isometric transformations, i.e., transformations that change orientation and transform ascending intervals into descending ones, and descending intervals into ascending ones. The only transformation that does not permit the conjunction of the original with the image, i.e., the congruence of the last point of the original with the first point of the image (for example, the last tone of the theme with the first tone of the variation) is retrograde transposition. Perhaps it is due to this very fact that the term "retrograde transposition", unlike other terms, does not appear in musical theory (see, for example, Skovran and Pericic, 1986). All of the mentioned isometric transformations are applied to an initial asymmetric figure (an elementary melodic entity, e.g., a motif). Since the result (product) of consecutive application of every two isometric transformations is a new isometric transformation, the existence of two isometric transformations within a melodic structure always results in the appearance of a third isometric transformation - their product, in the studied melodic structure. For this reason we will analyze the products of isometric transformations of a unison melodic structure:
With these compositions of isometric transformations of melodic structure in mind, one notes certain similarities and also crucial differences between two-dimensional geometric symmetry structures - plane ornaments, and melodic symmetry structures. The first difference is in the character of the effect of symmetry transformations: in the case of geometric symmetry structures the effect of transformations is global and results in complete periodicity and regularity of structure, which is not the case with melodic symmetry structures where the action of symmetry transformations is local, i.e., it refers only to individual melodic entities (Fig. 1.5) Another specific property of melodic symmetry structures is the non-equivalence of x and y-axis. As opposed to real infinite geometric symmetry structures (plane patterns) which have two equivalent infinite translations in the direction of the x and y-axes, in the melodic symmetry structures the directions of the x and y-axes are non-equivalent. The finite (modular) y-axis also causes specific limitations as to the position of the symmetry elements. Because of this, within unison melodic symmetry structures, individual elements of symmetry (otherwise present in two-dimensional geometric symmetry structures) do not appear as translations on the y-axis, mirror reflection mx with the mirror line parallel to the x-axis, etc. For this reason melodic symmetry structures that correspond to unison compositions may only conditionally be called two-dimensional. They are two-dimensional only when the position of each point (tone) is exactly defined by two coordinates (x1, y1). However, from the aspect of the equivalency of axes and the choice of the position of the elements of symmetry, they do not fulfill the conditions that a two-dimensional symmetric structure fulfills. We will show three examples to illustrate the isometric transformations of melodic structure (Figs. 3.19; 3.20; 3.21).
Figure 3.19 Retrograde repetition (mirror reflection m) as the basis of melodic structure: B. Bartok, Microcosmos, Vol. 1, Six Unison Melodies, part 6, (Apagyi, 1989).
|