|
Symmetry analysis of
rhythmic structure
We will illustrate the proposed
procedure with the example of a hypothetic rhythmic structure
(Fig. 2.5).

Figure 2.5
A hypothetic rhythmic structure prepared for a symmetry
analysis.
After assigning a corresponding
numerical value T(S)k to each measure, the most
important part of the task is the interpretation of the results.
In the case of the studied rhythmic structure we may draw the
following conclusions:
-
The distribution of numerical
values T(S): within the studied rhythmic structure made up
of sixteen measures, the numerical value of 6 appears four
times, the value of 20 appears once, the value of 18 appears
three times, the value of 24 six times and the value of 48
two times. The measures which correspond to equal numerical
values T(S) are permutationally equal, i.e., they share the
same rhythmic content.
-
The distribution of codes T(S)k:
the code 61 corresponds to the 1st, 15th and 16th measure,
which points to translational repetition. For T(S)=6, the
possible values of the lower index k are 1 and 2 (as [1/2]
and [1/4] can give only two possible arrangements). The code
62 corresponds to the 14th measure which points
to retrograde repetition. In the case where T(S)=18 the
possible values of the lower index k are 1, 2 and 3 (as
[1/2], [1/4] and [1/4] can only give three different
permutations with repetition). This means that within the
studied rhythmic structure all symmetry possibilities for
T(S)=18 have been used, in a cyclic order (181,
182, 183). The codes 181
and 183 which correspond to the 2nd and 8th
measure point to retrograde repetition. In the case of
T(S)=24 there are six possible permutations with the
repetition of elements [1/4], [1/4], [1/8], [1/8] and all
have been used. The pairs of codes 241 and 246
which correspond to the 5th and 11th measures and 242
and 245 which correspond to the 7th and 9th
measure point to the existence of retrograde repetition.
Because of the strictly periodical order of these codings
(243, 241, 242, 245,
246, 244) which correspond to the 3rd,
5th, 7th, 9th , 11th and 13th measure, retrograde repetition
represents not only local, but also global symmetry in the
substructure level. Finally, in the case of measures coded
as 484 (the 6th measure) and 4827
(12th measure), retrograde repetition is found.
-
The relationships between the
numerical values T(S): the sum of values T(S) which
correspond to the 1st and 2nd measure (6+18=24), when
multiplied by 2, gives 48. When we examine the order of note
durations we can conclude that the 6th measure can be
obtained by applying the method of diminishment, and that
the 12th measure is obtained by applying retrograde
diminishment on the first two measures. The sum of the
values T(S) which correspond to the 14th and 15th measure
(6+6=12), when multiplied by 2 gives 24. If we study the
order of the note durations we may conclude that these two
measures can be obtained by applying the method of
retrograde augmentation in the 3rd measure, and of
augmentation on the 13th measure. The same is true of the
15th and 16th measure. They can be derived by augmentation
from the 7th measure, and by retrograde augmentation from
the 9th measure. In terms of the half-phrases, it is
possible to see permutational repetition in half-phrases
5-6, 11-12, and 12-13, and in half-phrases 2-3, 3-4, 4-5,
7-8, 8-9, 9-10, 10-11. The same is true of 3-4-5, 7-8-9 and
for 5-6-7 and 11-12-13.
Finally, a more versatile
application of permutational proportionality is possible. We can
apply different proportional augmentations or diminishments with
the aim of obtaining a new rhythmic entity. For example, from
rhythmic entity S1=(1/2,1/4)
(to which diminishment has been applied) and rhythmic entities S2=(1/2,
1/8, 1/2) and S3=(1/4,
1/4, 1/8, 1/8)
(to which double diminishment has been applied) we obtain a new
rhythmic entity S=(1/4, 1/8,
1/8, [1/16],[1/16], [1/32], [1/32],
[1/32], [1/32]), and so forth. Although it does not pose major
problems, a detailed analysis of such procedures has been
omitted because of its extensiveness and a great number of
possibilities.
By applying this method it is
possible to analyze the symmetry of a rhythmic structure of real
musical pieces (Fig. 2.6)

Figure 2.6
The Art of the Fugue by J.S. Bach, an example of
diminishment (Skovran and Pericic, 1986).
The study of the symmetry of a
rhythmic structure within polyphonic musical pieces is reduced
to the study of the composition of linear symmetric structures.
Without straying away from a general approach, we can illustrate
this problem with an example of a two-part composition, In this
case, besides the already mentioned symmetry relationships that
exist between rhythmic structures within every linear component
(higher or lower voice), it is also necessary to examine the
symmetry transformations which translate the rhythmic entities
of one component to the rhythmic entities of a second component.
In this case, the following transformations of correlation may
occur:
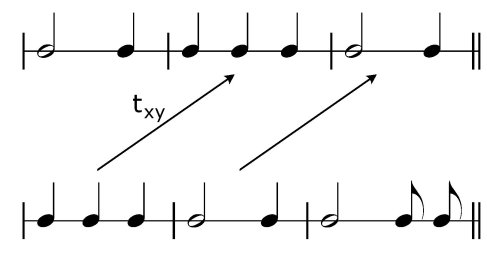
-
translation on the y-axis ty
(Fig. 2.7 a);
-
translation on the x and y-axes
tx,y (Fig. 2.7 b)
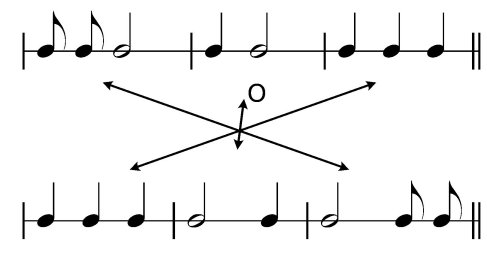
-
central reflection O (Fig. 2.7
c)

(a)
(b)
(c)
Figure 2.7
Symmetry transformations of a two-part rhythmic
structure: a) ty; b) tx,y; c) O.
The following group of
transformations of polyphonic musical pieces is made up of
transformations of proportionality. Each one of them can be
presented as an action of one of the mentioned isometric
transformations followed by a proportional augmentation or
diminution of all note durations that belong to the studied
rhythmic entity. Besides that, it is possible to study also the
permutational congruence or permutational proportionality of
rhythmic entities that belong to linear components (voices). By
defining the transformations that connect the linear components
it is possible to conduct a precise analysis of the different
aspects of complementary rhythms and polyrhythms which appear in
polyphonic compositions (Lemacher and Schroeder
1967, p. 21-22).
|



