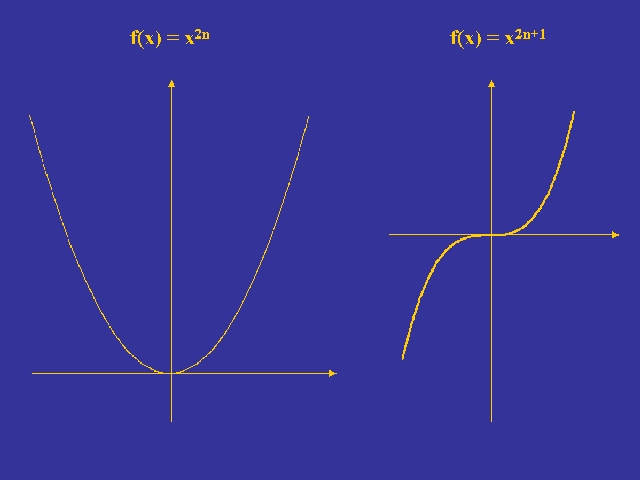COGNITIVE VISUALIZATION OF SOME INTEGER - VALUED POLYNOMIALS

Emiliano Ippoliti

University of Rome - "La Sapienza"

e-mail: e.ippoliti@srd.it

Abstract

Visualization is a powerful device in scientific discovery and in conjecture's formulation and it  has an increasing number of techniques and applications, revealing its cognitive and heuristic power.
A.A. Zenkin [Zenkin 1991] has found an interesting new propriety of square numbers, 1, 4, 9, 25,..., f(x) = x², x ÎN, using the so called phytograms, a cognitive and interactive visualization of number-theoretical proprieties.
In this paper I am going to show how such new graphical representation of number-theoretical objects can lead to find some new proprieties and formulate two analytical conjectures.
It will be shown, in particular, how visualization is essential to find new proprieties about some natural numbers series generated by integer-valued polynomials, i.e. f(x) = ax² ± bx ± c, where x, f(x), a, b, cÎN, and f(x) = xⁿ, i.e. f(x) = x²ⁿ⁺¹ and f(x) = x²ⁿ where x,n,f(x), n ÎN.
In §1 I will give a short introduction and will briefly describe Zenkin's result and his visualization's devices (CCG - Cognitive Computer Graphics).
In §2 and §3 we will present our visual results and conjectures about the above polynomials. 

§1 Introduction

§2 Visualization of second – degree integer - valued polynomials

§2.1 A first general conjecture

§3 Visualization of even and odd integer series

§3.1 A second general conjecture

Concluding remarks

References

§1 INTRODUCTION

           The well known relevance of formal proofs in mathematics cannot lead us to undervaluate the possibility of mathematical discoveries without proofs.
Visualization is traditionally seen (e.g. [Hadamar 1945]) as a valid mean of discovery, integrative or alternative to formalization and deduction, and as a powerful device in conjecture's formulation in mathematics. In fact not only it has an increasing number of techniques and plays a main role in many mathematical domains, like number theory, (see [Borwein and Jörgenson 1997], [Goetgheluck 1993], [Zenkin 1990]), but it is also the focus of epistemological ([Giaquinto 1994], [Giaquinto 1993]) and philosophical ([Brown 1997], [Horgan 1993]) debates.
Vision uses in fact very different cognitive processes from formal and abstract ones - i.e. geometrical construction and gestalt principles, recognition of patterns, space symmetries, etc. – that are able to induce data organization that lead to find new, unexpected mathematical proprieties and formulate fruitful conjectures.
Moreover my results are going to show how it lays not simply on something like direct perception, but how it needs some kind of “interpreting”.
Problem solving, hypothesis’s and conjectures formulation and mathematical discoveries in fact often arise from change of codification of knowledge, both formal both graphical: this apparently simple transformation allows in fact to treat mathematical problem or concept like an object in a open conceptual system [Cellucci 1998, Cellucci 1992], where its many, different, codification cooperate and interact during the solution or discovery  process.
"However the history of mathematics is marked by many notable developments grounded in the visual. Descartes' introduction of 'cartesian' co-ordinates, for example, is arguably the most important advance in mathematics this millennium"([Borwein and Jörgenson 1997], pag.1).The famous interpretation of algebraic equations like bi-dimensional curves, and vice versa, allows in fact Descartes, and separately Fermat, to make interesting mathematical discoveries and solve long standing problems: they fruitfully link two different mathematical disciplines (i.e. algebra and geometry) and create a new domain and a new codification of knowledge.
In number theory, however, is well known how visualization of figurate numbers (i.e. triangular numbers, squares numbers, pentagonal numbers, etc.) heavily helps Pythagoras to find beautiful and relevant arithmetical laws.
           Thus it seems to be no doubt, in general, on heuristic nature, and power, of visualization. So the real question seems to be: can visualization be a mean of discoveries of analytical truth? can it, finite and empirical, allow to find evidences for infinite and abstract processes?
There are, obviously, notorious and traditional limits of visualization that can be adduced as strong arguments against not only its heuristic role, but also its local, naïve and didactic use: the number of data that can be visualized, the few available dimensions, the empirical nature are often really big theoretical and practical obstacles of images, that can do us error steps or lead to false inference (see e.g. [Brown 1997] the case of four circles in dimension n, for n>10).
Moreover visualization seems to bring to mind only single cases and particular examples, that are unable to reach the abstractness and the generality necessary to create new, relevant mathematical knowledge.
Giaquinto ([Giaquinto 1994], [Giaquinto 1993]) argues nevertheless that visualization allow inner experiments and can make emerge both schemes (of operations or analytical proofs) and the possibility of certain relationship at least in arithmetic and in elementary real analysis: he shows, discussing two famous Litllewood’s examples – fixed point’s theorem and intermediate value’s theorem - how visual thinking, although rarely a method of discovery, can be a stimulus to discover.

But there is a more radical and fine question about visualization, that has obviously only limitative and local answers, if any.We can express it in the following way: does visualization occur in every discovery or proof? Does visual thinking, and the ability to create and operate on images and space, support every both logical and intuitive mental operations? Is it possible to suppose that there is a geometrical – graphical component in every mathematical reasoning?

It obviously doesn’t mean that every mathematical concept or idea has a specific visual representation, but rather that is possible in some way to express graphically concepts, solvability’s conditions, terms and relationship ofproblems and concepts.

In this paper I first of all try to give a positive, but very local, answer to above questions, showing with some examples in number theory how just cognitive visualization is not a superfluous "correlate" of mathematical thought, but how it can play an essential and cognitive role in mathematical discovery's process.

It is worth noting that number theory isn’t a casual choice: numbers in fact, as noted by [Giaquinto 1993], seem to be pure abstract objects, entities that are also potentially not visualizable.

Then I will try to illustrate how visualization and images can be not only a valid means of discovery and creation of new knowledge, but also how it can allow to overcome some limits of formalist and deductive approach in mathematics.

A.A. Zenkin [Zenkin 1991] found an interesting and unexpected propriety of square numbers 1, 4, 9, 25, ..., f(x) = x², ÎN, using a visual representations called phytograms - a kind of cognitive computer graphics (CCG).

Phytograms are a way to build a new kind of visual representations of number theoretical proprieties - a new codification of knowledge - : they visualize in a bi-dimensional table a discrete domain and create visual objects that can be studied visually, interactively and in a "virtual geometry" environment.

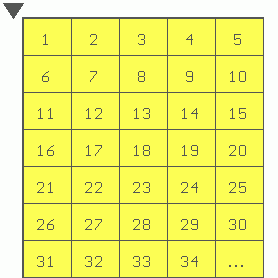
To construct a phytogram, first of all, we rewrite the 1D-sequence 1, 2, 3, 4, 5,..., n, nÎN, in the following 2D-form (see Figure 1):

Figure 1

Let the modulus (mod) be the quantity of numbers-cells in every string of the phytogram (in the example given in Figure 1, so, mod = 5).
Now we can choose any propriety of natural numbers, expressed by a predicate P(n), and visualize it on a phytogram according to the following rule:

if P(n) is true, then the color of the n-th cell is, e.g., black, else

if P(n) is false, then the color is, e.g., yellow

Let P(n) = "to be or not be a square of a natural number" , n = x²: for mod = 5 we obtain the following pythograms – e.g. by Zenkin [Zenkin 1991] – (see Figure 2):

Figure 2

The phytogram is able to show the twice abstract connection between two main proprieties of number theoretical objects - the additive and multiplicative.
The former is expressed by the colors of the phytograms , the latter by the position, since all numbers n, for which n = (k x mod) + j, j < mod, holds, are in the same j-th column of the pyhtogram.
           Increasing or decreasing the modulus, we obtain several configurations (structures) of the same number - theoretical propriety P(n) that can be a useful heuristic device: at the beginning we can obtain disordered sets of, e.g., black and yellow points, but often we can see sets showing certain loop or structures that, suitably interpreted, reveal very interesting patterns or models.
For ‘suitably interpreted’, we means that such patterns are not simple, direct "data", but that they often emerge by, and need, a "see" able to find analogies, links and correspondences between  a phytogram's set of points and space structures of other scientific disciplines or mathematical domains (like geometry, biology, etc.).
Using a famous Wittgenstein’s distinction [Wittgnestein 1953], when we observe images, like phytograms, and give them a sense, we are always in a “see as” not simply in a “see”. As noted by Brown ([Brown 1997]), visualizing and interpreting also a mathematical object implies a "metaphorical look", that is extended to an entire class of objects.
           So just using CCG and suitable visual interpreting A.A. Zenkin [Zenkin 1991] has found a "beautiful and unexpected" propriety of square numbers 1, 4, 9, 25, ..., f(x) = x², x ÎN, that reveals a transformation not known in modern mathematics.
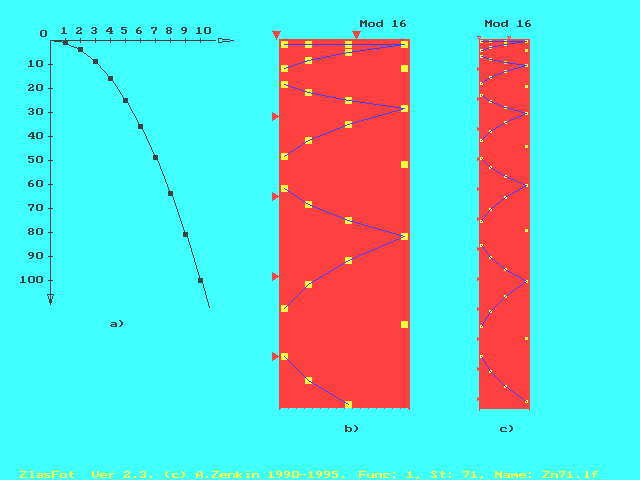
In fact for mod = 16, the single but infinite parabola x² , see Figure 3a, became an infinite family of finite parabolas, Figure 3b-c, that can be formalized - as easily verifiable - in the following way: Y#(n) = (8n ± k)² , nÎN, k = 0,1,2,3,4.
As can be seen in Figure 3 each parabolas has nine points that are squares of successive natural numbers.

Figure 3

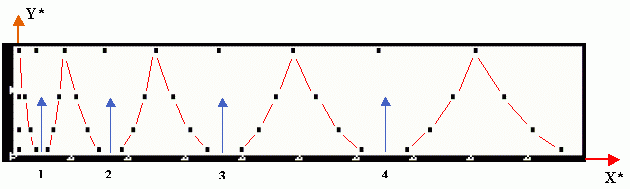
We can formalize and express analytically the family by associating a local coordinate system to the pythogram (as shown in Figure 4); thus, we have Y#(n) = (8n ± k)2 , nÎN, k = 0,1,2,3,4 where each point n is a parabola number: in fact the value of Y#(n) here is not a usual number, but the sequence of following nine squares of successive natural numbers (8n-4)² , (8n-3)² , (8n-2)² , (8n-1)² , (8n)² , (8n+1)² , (8n+2)² , (8n+3)² , (8n+4)² for n = 0,1,2,3...
So the infinite family of finite parabolas is the following infinite sequence of 9-points parabolas: Y#(0), Y#(1), Y#(2), Y#(3), ... Y#(n).

Figure 4

 

§2 VISUALIZATION OF SECOND - DEGREE INTEGER - VALUED POLYNOMIALS

           Zenkin's result shows how the main geometrical structure of the square numbers series - i.e. the parabola - appears both in Cartesian representations and in CCG - space (so the main structure remains unvaried), revealing a new connection between finiteness and infiniteness.
We found an interesting similarity w.r.t. phytogram of x² visualizing two natural numbers well-known series: the so called "etheronomechial" and "planic" numbers, respectively n = x² - x and n = x² + x, both geometrical parabolas (instance of polynomials of form f(x) = ±ax² ± bx ± c).
It is worth noting that we will consider only integer-valued polynomials (generating integer numbers series), that satisfy the conditions x > b, x² > c, -ax² < ± bx ± c, ax² > ±bx ± c: so x² + x and x² – x express the same series and in general dual polynomials express the same series (e.g. x² + 4x generates the same series of x² - 4x, because we consider, for the latter, only x’s values > 4, generating integer natural numbers).
The predicate used to construct the phytograms is therefore P(n) = 'to be or not be a planic/heteronomechial number".
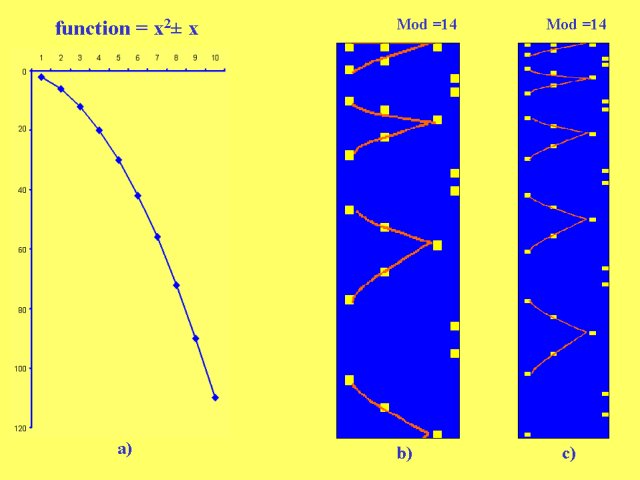
For mod = 14, as shown in Figure 5, the series became an infinite family of finite parabolas, each of 8 points that are successive planic (etheronomical) numbers, such that for every nÎN, k = 0,1,2,3 , holds Y#(n) = (7n ± k)² + (7n ± k), or (7n ± k)² - (7n ± k), where, for n³1, -k = 4, and for, n = 0, obviously we consider only positive values of ± k in the second member of the equation.

Figure 5

Here we have again a single but infinite parabola that became an infinite family of finite parabolas, trough the same connection between infiniteness and finiteness from Cartesian system to CCG - space of square numbers series.
This result lead us to extend the visual study to natural numbers series that are generally expressed by parabolas, say second – degree integer – valued polynomials, n = ax² ± bx ± c, a,b,c,x,nÎN.
In Table 1 we summarized only some results reached visualizing numbers series generated by such polynomials and shows how for this cases always exists a mod's value such that the transformation holds.

 

Table 1

 

§2.1 A FIRST GENERAL CONJECTURE

The above visual observations and results suggest the following conjecture: given any natural number series generated by polynomials of he form n = ax² ± bx ± c, a,b,c,x ÎN, there always will be a mod's value such that exist an infinite family of finite parabolas, each of j ± k points, expressed by an equation of the form a(jn ± k)² + b(jn ± k)+ c, a,b,c,j,k,n,xÎN.
It means that it will always possible to express a series n = ax² ± bx ± c in the form a(jn ± k)2 + b(jn ± k)+ c and represent the single, infinite, Cartesian parabola like an infinite family of finite parabolas in CCG - space.
More formally:

(I)      "(ax² ± bx ± c), a,b,c,x ÎN,$ mod s.t. $ infinite family of finite ax² ± bx ± c of form Y#(n) = a(jn ± k)² + b(jn ± k)+ c

where a,b,c,j,k,n,xÎN and j ± k = points of single finite ax² ± bx ± c.

It is worth noting that such transformation holds reversing the relationship between finiteness and infiniteness, and we will see how it will play a main role also in formulation of our second conjecture.

 

§3 VISUALIZATION OF EVEN AND ODD INTEGER SERIES

Let now visually inspect by phytograms the following series 1, 8, 27, ..., f(x) = x³, x ÎN, using therefore the predicate P(n)= "to be or not be a cubic number".
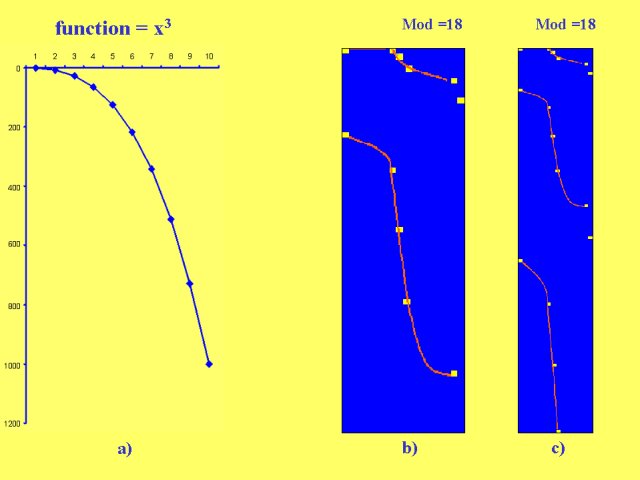
For mod = 18, see Figure 6, we obtain a really interesting result: like x², in fact, here we have a single, finite, infinitely iterated structure.

Figure 6

Unexpectedly the shape of iterated finite structure is exactly a cubic, and the infinite family is expressed, in the local coordinate system, by the equation Y#(n) = (6n - k)3 , nÎN, k = 5,4,3,2,1,0, where each cubic n has six points, successive cubes of natural numbers, (6n-5)³ , (6n-4)³ , (6n-3)³ , (6n-2)³, (6n-1)³ , (6n)³.
Thus, like x³, by the single cubic series 1,8,27,..., x³ we obtain an infinite family of finite cubics.
So for n = 2 and n = 3, we have two similar and interesting results for series of natural numbers of the form xⁿ , x,n ÎN.
Visualization of successive values of n in xⁿ reveal not only a strong similarity w.r.t. this results, but will also lead us to formulate a successive conjecture.
           Let begin by n = 4, phytograms with P(n) = "to be or not to be a bi-square of a natural number".
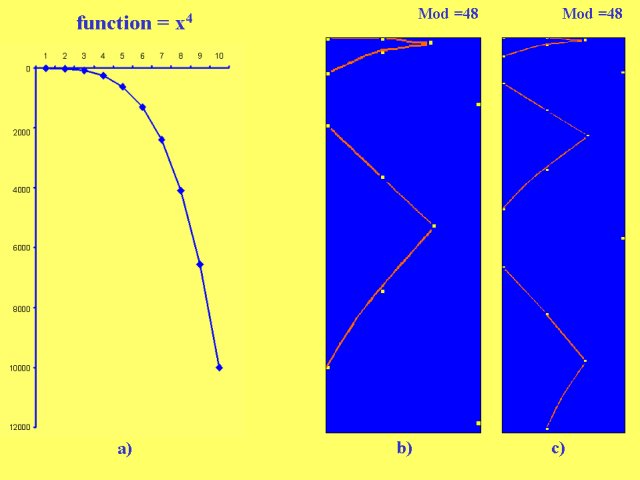
Visualizing the bi-square series 1, 16, 81, 256, ... , x⁴, x ÎN, in fact, we obtain, for mod = 48, (see Figure 7a) another space configuration similar to the previous: an infinite family of finite parabolas - having obviously a greater concavity than the square numbers series -, each of 7 points successive bi-squares of natural numbers (4n - 3)⁴ , (4n - 2)⁴, (4n - 1)⁴ , (4n)⁴ , (4n + 1)⁴ , (4n + 2)⁴ , (4n + 3)⁴, expressed in local coordinate system by the equation Y#(n) = (4n ± k)⁴, nÎN, k = 0,1,2,3.
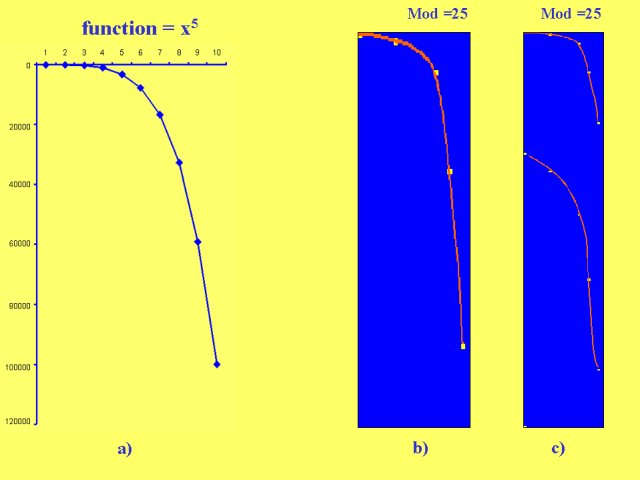
For n = 5 indeed, P(n) = "to be or not to be a fifth powers of a natural number", we obtain an interesting visualization similar to n = 3 (see Figure 7b).
The series of fifth powers of natural numbers 1, 32, 243, 1024, ... , x⁵, x ÎN, shows again, for mod =25, an infinite family of finite structures that resemble cubics, each composed of 5 points, successive fifth powers of natural numbers, (5n - 4)⁵ , (5n - 3)⁵ , (5n - 2)⁵ , (5n - 1)⁵ , (5n)⁵, expressed by the equation Y#(n) = (5n - k)⁵ , nÎN, k = 4,3,2,1,0.
The series assumes, in detail, the typical course of odd functions: this visual fact, on the base of the results summarized in Table 2, suggests the conjecture of the following paragraph.

Figure 7a

Figure 7b

Table 2

 

§3.1 A SECOND GENERAL CONJECTURE

As known, even and odd functions, f(x) = xⁿ, x, nÎN, for n > 1 and respectively n = 2p and n = 2p+1, have typical and different courses in Cartesian plane (see Figure 8).

Figure 8

Now for n = 2,3,4,5 we saw that exist at least one transformation in CCG - space that change the single, infinite, cartesian structure in an infinite family of finite structures that have the same course of the Cartesian ones.
It seems plausible to suppose that such transformation holds for every odd and even series.
It means that it will always be possible to represent a single, infinite, odd/even series of natural numbers like an infinite family of finite, respectively, odd/even structure, expressible in the form Y#(n) = (an ± k)^N N ,a ,k,n,ÎN, a ± k = number of points of single finite structures.
More formally:

(II)    " xⁿ, x,n ÎN, $ mod s.t. $ infinite family of finite xⁿ of form Y#(n) = (an ±k)N N ,a ,k,n,ÎN, 

where a ± k = number of points of single finite xⁿ that have, for n = 2p and n = 2p+1, respectively an even and odd structure. 

Concluding it is worth noting that: 

(a)               both conjectures have an existential form ( For every …it exist a mod’s value such that …): they look for at least a single mod’s value that satisfy the propriety.

Obviously visual inspection of number theoretical proprieties can assume an universal form. In fact we can look for invariants (also topological) that occur in every mod’s value (i.e. in every phytograms): given a number theoretical relationships, we can thus look for proprieties of form “ for every mod’s value it exist a etc. etc.” (examples of such kind are given in [Zenkin 1999 ]).

(b)               their formulation strictly depends on visualization, that enable us to see and construct space relationships and patterns that suggest their recognition.  It’s difficult in fact, if not impossible, to reach them adopting the deductive and formalist research’s style: so visualization not only shows its heuristic power but also reveals its deep utility in creation of new knowledge.

 

CONCLUDING REMARKS

"Mathematics can be described as a ‘science of patterns’, pursuing patterns, relationships, generalized descriptions and recognizable structures in space, numbers, and others abstracted entities"([Borwein and Jörgenson 1997], pag.1). 
The above results have been reached applying a methodology and a heuristic approach (typical of visual thinking) that is not really usual in a very abstract, formalized and traditional domain like number theory.

In fact it visually looks for such patterns and relationships overriding the formalist and deductive way: it takes a number theoretical series, expressed by a sentence P(n) and by its own representation in Cartesian plane, and change visualization’s system by phytograms. This simple operation allows to transform an integer numbers series in a new, essentially geometrical object that can be examined visually and graphically, finding new structures and proprieties using visual data – organizer principles like symmetries, connection, space analogies, etc.

In particular, interaction with visual facts (values of mod’s phytograms) led us to find (see) some patterns that we tried to recognize analogically in similar integer numbers series to obtain a more general conjecture and formal proprieties.

Then, founded such correspondences, we use ordinary formal devices to formulate inductively two general conjectures that seem to specify new interesting proprieties of such integer numbers series.

We noted that visualization is essential to reach this results: it is impossible to obtain them applying ordinary formalist and deductive tools, unable tosuggest the existence of such transformations form Cartesian to CCG - space.
Although it is a not conventional methodology, cognitive computer visualization (CCG) by phytograms is a new fruitful way of study and interact with number theoretical objects that can be successful applied, as heuristic device, in discrete domain and that can be very useful not only in modern [Zenkin 1990], but also in long standing number - theoretical problems.
I mean that cognitive visualization allow to study and interact with - number theory in several ways, looking for both existential and universal theorems and conjectures, and show how visual thinking and visual procedures can be not only a powerful resource, but often an absolute necessity for mathematical creativity.

ACKNOWLEDGEMENTS

I would like to thank prof. A.A. Zenkin for his precious advices and doc. U. Rustichelli for his help in software development under Linux.

 

REFERENCES

[Borwein and Jörgenson 1997] Visible Structures in Number Theory, Peter Borwein and Loki Jörgenson, preprint submitted for pubblication, CECM, http://www.cecm.sfu.ca/~loki/Papers/Numbers/, 1997.

[Hadamar 1945] The psychology of invention, Jacques Hadamar, Princeton University Press, 1945.

[Goetgheluck 1993] Fresnel zones on the screen , Pierre Goetgheluck, Experimental mathematics, Vol. 2 , 1993, No. 4, pagg. 301-309.

[Zenkin 1990] Waring's problem from the standpoint of the cognitive interactive computer graphics , A.A.Zenkin , An International Journal - Mathematical and Computer Modeling, Vol.13, No. 11, pp. 9 - 25, 1990.

[Zenkin 1991] Cognitive Computer Graphics. Applications in Number Theory, A.A. Zenkin, Moscow: "NAUKA", PhysMath. Literature, 1991, 191 pp.

[Zenkin 1999] [Zenkin 1999] Virtual Geometry of Natural Numbers, http://www.com2com.ru/alexzen/papers/vgeom/vgeom.html

[Brown 1997] Proofs and pictures , J.R. Brown, Brit. J. Phil. Sci., 48:161-180, 1997.

[Giaquinto 1994] Epistemology of visual thinking in elementary real analysis, Marcus Giacquinto, Brit. J. Phil. Sci., 45, 1994.

[Giaquinto 1993] Visualizing in Arithmetic, M. Giaquinto, Phil. Phenom. Research, 1993.

[Horgan 1993] The death of proof, John Horgan, Scientific American, 269, n.4, October 1993.

[Cellucci 1998] "Le ragioni della logica", Carlo Cellucci,  Laterza, 1998, 420 pp.

[Cellucci 1992] "From closed to open systems", Carlo Cellucci, Proc. of th 15^th International Wittgenstein-Symposium, Czermak, 1992, pagg. 206-220.

[Wittgnestein 1953] “Philosophische Untersuchungen“, L. Wittgenstein, (1953), Philosophical Investigations, translated by G. E. M. Anscombe, 3rd edition, 1967, Oxford: Blackwell