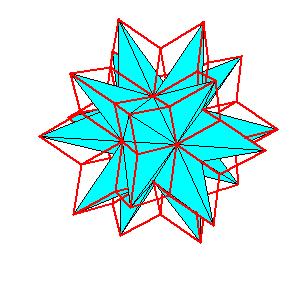
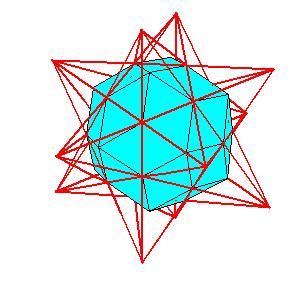
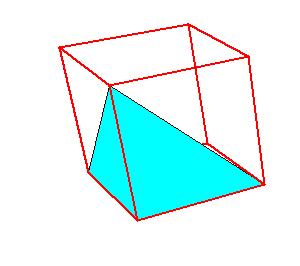
We observe that the combination of the small stellated dodecahedron and of the great stellated dodecahedron can be dissected to combination of the rhombic triacontahedron and of the hexecontahedron. In [2] we have shown that the combination of the icosahedron, the dodecahedron and the icosidodecahedron can be dissected to combination of the triacontahedron and the hexecontahedron. In this way we answered the question posed in [1, pg. 231]. If we consider the small stellated dodecahedron as built from the dodecahedron and of a layer of 12 pentagonal pyramids, and consider the great stellated dodecahedron as built from the icosahedron and of a layer of 20 triangular pyramids, then these pyramids should form the icosidodecahedron (or the small icosihemidodecahedron and the small dodecahemidodecahedron). But we could observe the surplus of 60 (non regular) tetrahedra of small stellated dodecahedron over the triacontahedron and deficit of these solids of the great stellated dodecahedron relative to the hexecontahedron. The mentioned tetrahedra are 1/6 (in volume) of prolate golden rhombohedron.

| 
| 
|
References
[1] J. H. Conway, C. Radin, and L. Sadun, On angles whose squared trigonometric functions are
rational, Discrete & Computational Geometry, 22 (1999), pages 321-332.
[2] I. Hafner, Live3D Animation to Solution of Conway-Radin-Sadun problem, Visual Mathematics, Volume 9, No. 1, 2007 ,1