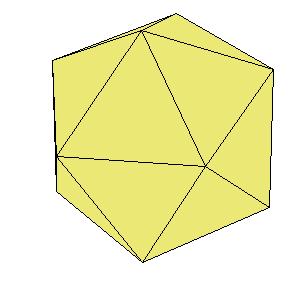
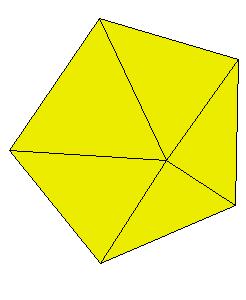
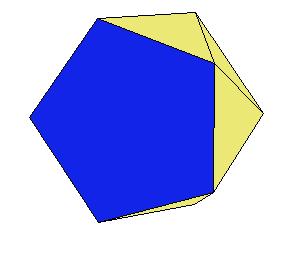
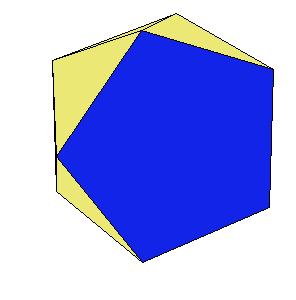
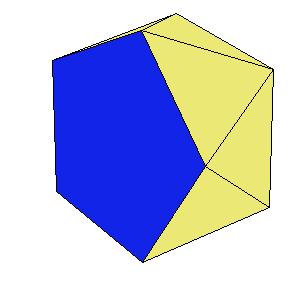
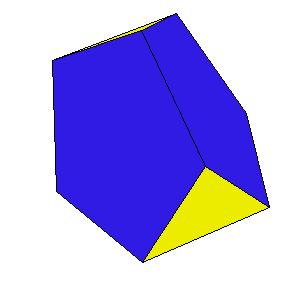
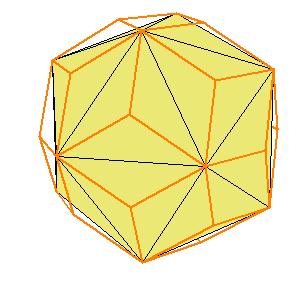
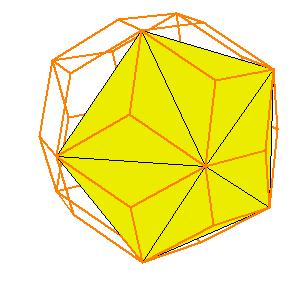
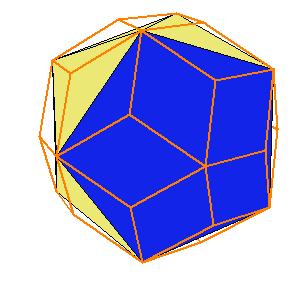
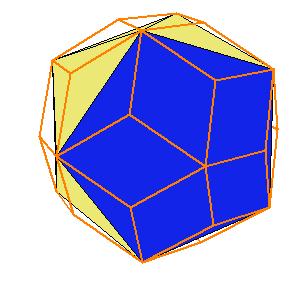
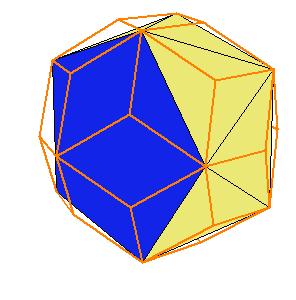
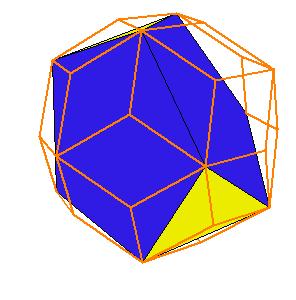
If a pentagonal pyramid (Johnson solid 2) is cut off the icosahedron , we get the gyroelongated pentagonal pyramid (Johnson solid 2: J2). If we cut off another pentagonal pyramid, we get either a pentagonal antiprism or a metabidinimished icosahedron (J62). If we cut three pentagonal pyramids, we get a tridiminished icosahedron (J63).Click on the picture to activate Live3D graphics [3].

| 
| 
|

| 
| 
|

| 
| 
|

| 
| 
|
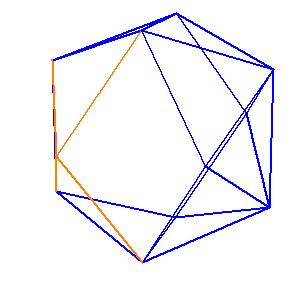
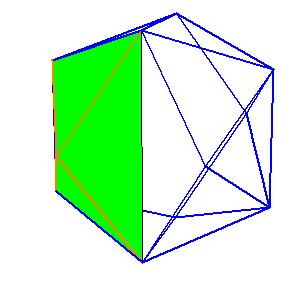
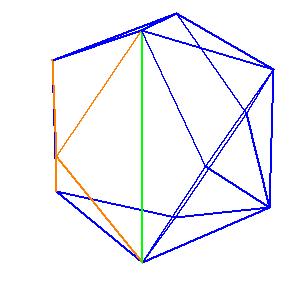
It is obvious, that the pentagonal antiprism and the metabidinimished icosahedron have the same volume. But they have the same complement relative to the rhombic triacontahedron, namely the complement consists of 2 pentagonal cups and 10 triangular pyramids. This means they are equidecomposable [1].
| 
| 
|
| 
| 
|
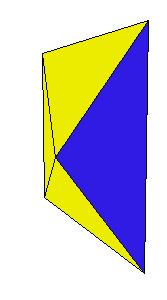
To make a paper model use the following nets: