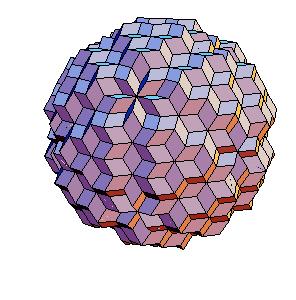
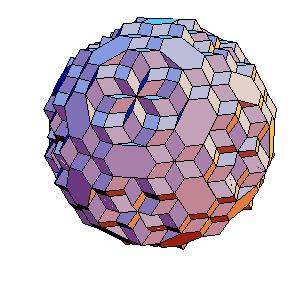
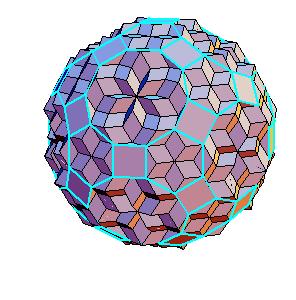
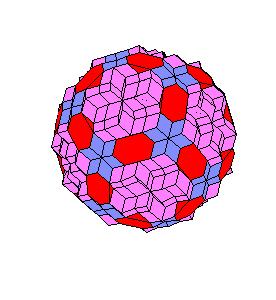
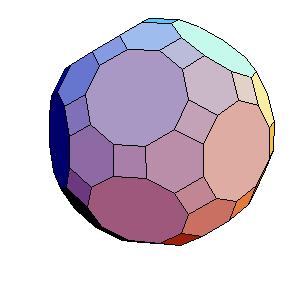
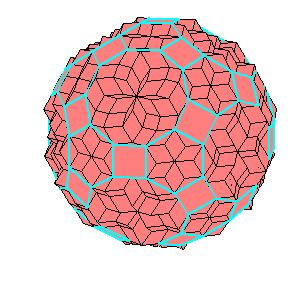
Abstract
For the truncated icosidodecahedron we construct its best “rhombic approximate” and show that there is a hinged dissection of one to another. By rhombic solid we mean a polyhedron that consists of prolate and oblate golden rhombohedra. In the solution we also use halves of rhombic dodecahedron of the second kind, which in turn consists of two halves of the rhombohedra.
Introduction
In [2, pg. 331] J. H. Conway, C. Radin and L. Sadun
applied their theory of geodetic angles to the non-snub Archimedean polyhedra proving that
the following combinations of Platonic and Archimedean solids can be decomposed to a cube.
Truncated icosidodecahedron
Icosahedron + Truncated dodecahedron
Dodecahedron + Truncated icosahedron
Icosahedron + Dodecahedron + Icosidodecahedron
Icosidodecahedron + Rhombicosidodecahedron
Truncated icosahedron + Truncated dodecahedron + Rhombicosidodecahedron
The problem is, how to perform such dissections. For each of the above combinations we found
an equidecomposable combination of rhombic solids [11].
In fact there are essentially two solutions depending on the length of edges of the Archimedean solid,
which may be shorter or larger diagonal of the rhombus.
In this paper we present some details of hinged dissection [3] of a “rhombic” solid to the
truncated icosidodecahedron.
Case 1. The edge equals the larger diagonal.
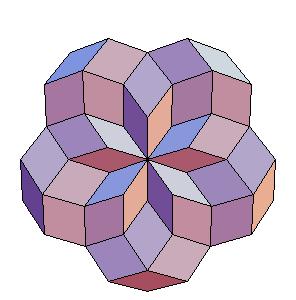
The “rhombic” solid is obtained by addition of 30 halves of rhombic dodecahedron of the second kind to a rhombic 690-hedron. Since rhombic solids consists of prolate and oblate rhombohedra and a half of rhombic dodecahedron consists of two halves of both rhombohedra [8,9], the “rhombic” solid can be dissected to a cube [1]. Animations use Martin Kraus' Live3D applet [12]. Click on a picture to invoke the animation.
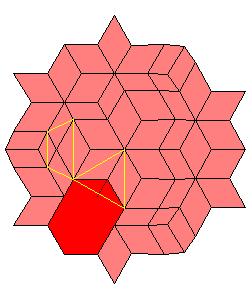
690-hedron, augmented with 30 halves of the rhombic dodecahedron of the second kind.

| 
| 
|

| 
| 
|
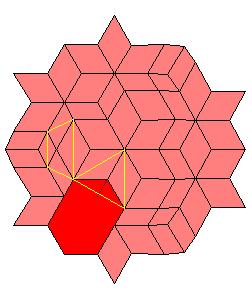
Situation around triad axes.
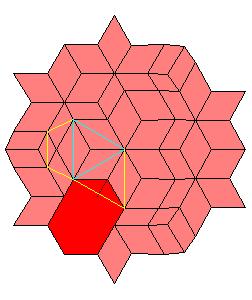
| 
| 
|
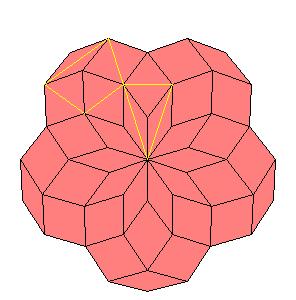
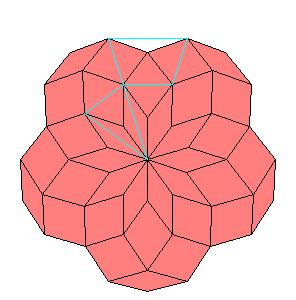
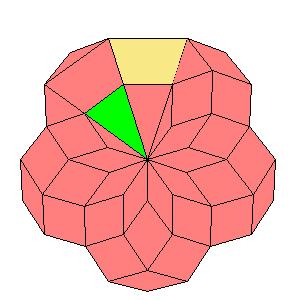
Situation around pentad axes [is the same as in 10].
| 
| 
|
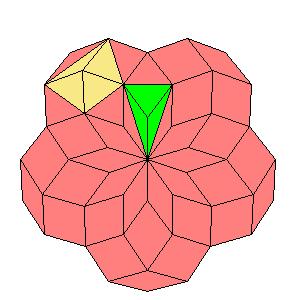
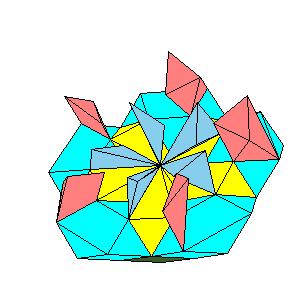
| 
| 
|
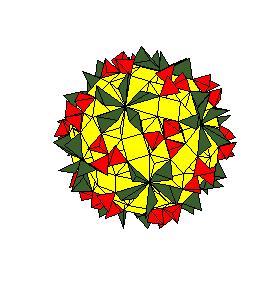
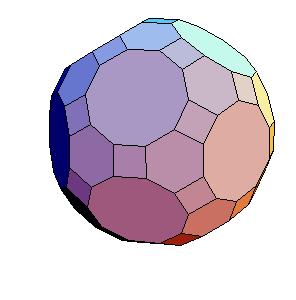
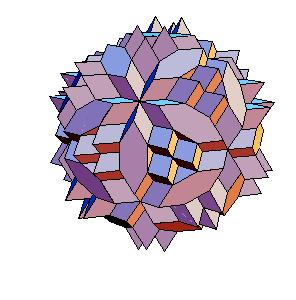
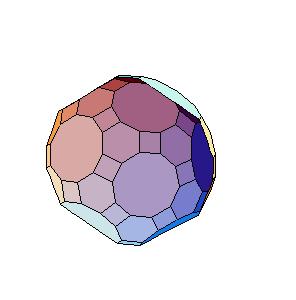
Case 2. The edge equals smaller diagonal.
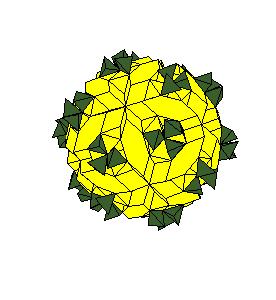
| 
| 
|

| 
| 
|

| 
| 
|
References
[1] V.G. Boltjanskii, Tretja problema Hilberta, Nauka, Moskva 1977.
[2] J. H. Conway, C. Radin, and L. Sadun, On angles whose squared trigonometric functions are rational, Discrete & Computational Geometry, 22 (1999), pages 321-332.
[3] G. N. Frederickson, Dissections: Plane & Fancy, Cambridge U. Press, 1997.
[4] I. Hafner, T. Zitko, A dissection of quarter of rhombic dodecahedron of the second kind to a cube, http://torina.fe.uni-lj.si/~izidor/RhombicPolyhedra/RhombicPolyhedra.html
[5] I. Hafner, T. Zitko, Introduction to golden rhombic polyhedra - published in Visual Mathematics Vol.4, No.2, 2002, 2, (3)
[6] I. Hafner, T. Zitko, Relations among rhombic, Platonic and Archimedean solids - published in Visual Mathematics Vol.4, No.2, 2002, 2, (4)
[7] I. Hafner, B. Jurcic-Zlobec, T. Zitko, Gallery of rhombic polyhedra, - published in Visual Mathematics Vol.4, No.2, 2002, 2, (4)
[8] I. Hafner, T. Zitko, A dissection of two rhombic dodecahedra of the 2. kind to a cube, Volume 8, No. 3, 2006 ,1
[9] I. Hafner, T. Zitko, A dissection of quarter of rhombic dodecahedron of the second kind to a cube, Volume 8, No. 3, 2006 ,2
[10] I. Hafner, T. Zitko, I. Hafner, T. Zitko,Hinged dissection of a half of rhombic icosahedron
[11] I. Hafner, Live3D Animations to Solution of Conway-Radin-Sadun Problem,Visual Mathematics, Volume 9, No. 1, 2007 ,1
[12] Martin Kraus' Live3D applet http://www.vis.uni-stuttgart.de/~kraus/index.html