
»The study of polyhedra is an ancient one, going back to the dawn of history. It is especially those that are called uniform that have evoked the greatest interest and provided the most fascination. It should be of special usefulness for mathematics students and teachers in their classrooms today to see and handle these geometrical solids in aesthetically pleasing models and to be delighted with their beauty and form. « [M. J. Wenninger, Polyhedron Models for the Classroom, NCTM, Reston, 1966]
In order to stimulate students to study polyheda we designed two sets of problems on the solids [1]. The first set consists of labyrinths on the solids, the second of colouring them. Both problems are available as java applets on internet [ International Space Visualization Olympiad, competitions and tests].
Organizers of mathematical competitions are always challenged by problem to construct new type of problems or to make variations of old ones. Additional limits are also posed by multiple choice format contests. While preparing competitions in recreational mathematics we face the following demands on the type of problems: the problems are to be easy to understand, should be of various difficulties, must be technically hard to produce by hand and the number of variations should be very large. In fact we are looking for problems to be made by a computer.
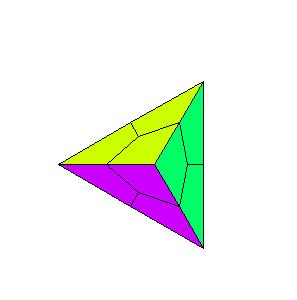
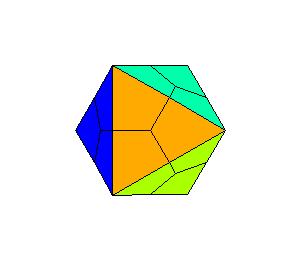
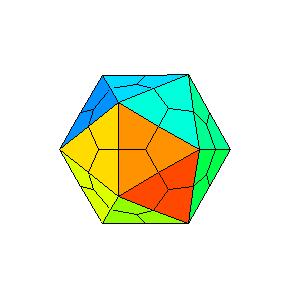
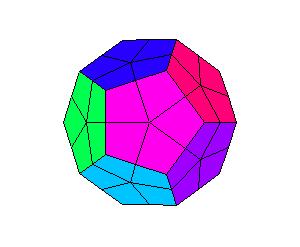
The idea for one kind of such problems is quite a simple one. Given a polyhedron, colour its faces by different colours, divide faces on smaller polygons and unfold the new polyhedron into a random plane net. In this paper we shall divide each face by connection of the center with midpoints of the sides.
Although we are not limited by the type of polyhedra, we shall illustrate the procedure on Platonic solids. A click on an illustration will invoke LiveGraphics3D animation of unfolding a divided Platonic solid into a net.
The colour of only one polygon of each face is shown. The task is to colour the other polygons. To illustrate the problem, we are asking for the proper colour of the black quadrilateral. After the guess run the animation to check the answer.
The problem gets even harder if we do not give the initial set of coloured quadrilatrals. The task is to colour all polygons that belong to the same face, with the same colour. The illustrations bellow show the problem on an octahedron.
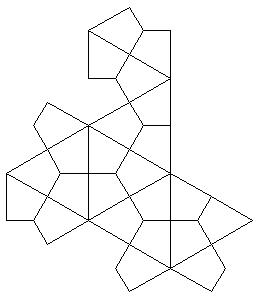
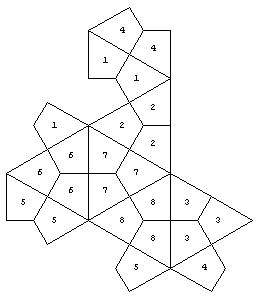
For the purpose of the mathematical competitions the problem may be posed in the form of multiple choice question:
Problem: The faces of the tetrahedron are coloured by different colours marked by integers. The faces of the solid are then divided on smaller polygons and the new solid is developed into a net. The colour of only one polygon of each face is shown. To which set the colour of the polygon marked by ? does belong?
(a) {1} (b) {2} (c) {3} (d) {4} (e) {5}
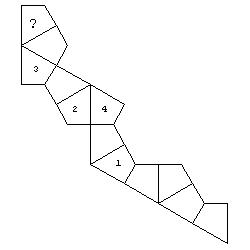
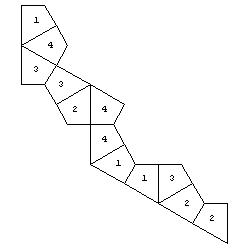
Answer: a
Solution: 1
Note that the above problem is entirely generated by a computer.
We are not concerning with methods of solving such questions, but we note some of them may be quite trivial and the other may consume same time. Since our program works for any polyhedron, that we could divide faces into even smaller parts and that the number of nets is very large, we have here a type of problems we are looking for.
Here
you will find two sets of 25 problems of the last two types.
[1] Hafner, I: Colouring polyhedra and Labyrinths an Polyhedra
, Mathematics in School, September 2001, Vol. 30,
No. 4, pgs.8-9
[2] http://Olympiad.fe.uni-lj.si