There are two ways to improve teaching of stereometry using computers. Moving 3-D graphics are allmost as good as real models in three-dimensional space. But the best way to learn about geometric models is to make them. Nets for models made by computer programs are more accurate then ruler amd compass constructions. In this paper we take examples from Euclid's Elements. Text is from [1], where illustrations use java scripts and from [2]. We try to mimic illustrations from [2] using Live3D applet developed in [3].
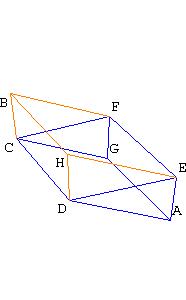
Book XI, Proposition 28.
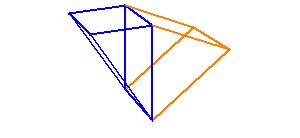
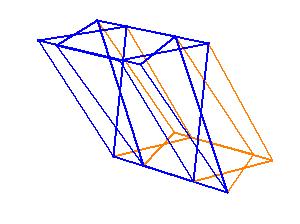
If a parallelepipedal solid is cut by a plane through the diagonals of the opposite planes, then the
solid is bisected by the plane.

|
Comment.
The prisms are only symmetrical, that they are equivalent certain propositions are necessary
[2, pgs. 331-333].
| 
| 
|
| 
| 
|
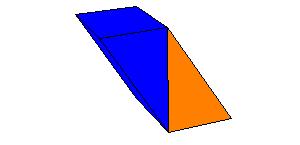
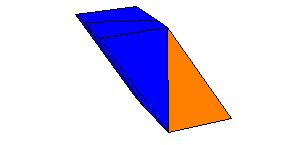
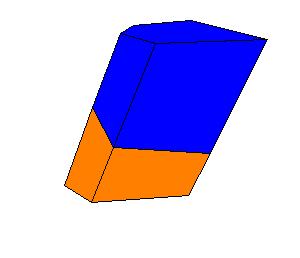
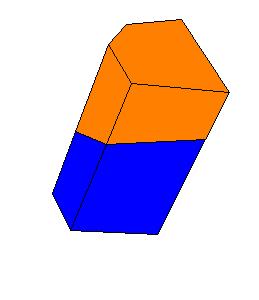
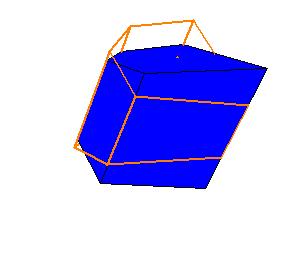
An oblique prism is equivalent to a right prism whose base is a right section of the oblique prism and whose height is equal to a lateral edge of the oblique prism.
| 
| 
|
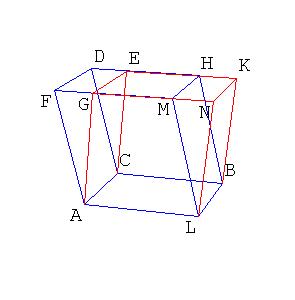
Proposition 29.
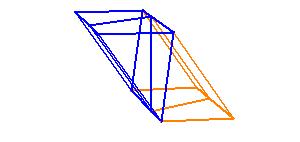
Parallelepipedal solids which are on the same base and of the same height, and in which the ends of their
edges which stand up are on the same straight lines, equal one another.
| |
| 
|
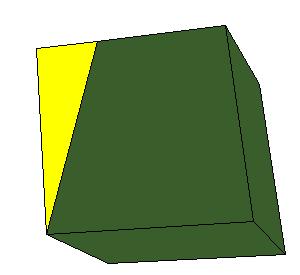
Proposition 30.
Parallelepipedal solids which are on the same base and of the same height, and in which the ends of their
edges which stand up are not on the same straight lines, equal one another.
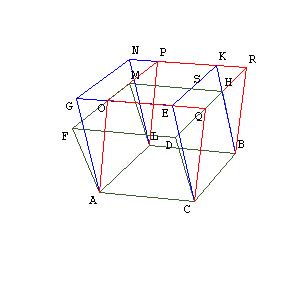
|
|
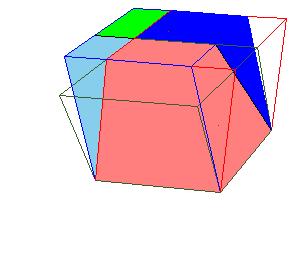
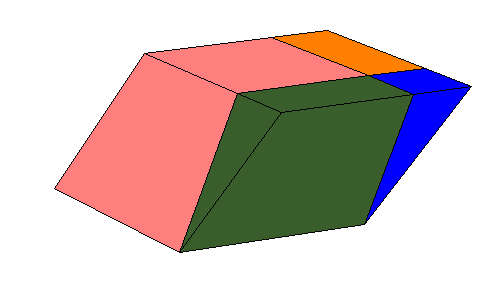
Legendre deduced useful theorem that [2, pg. 335]:
Every parallelepiped can be changed into equivalent rectangular parallelepiped having the same height
and an equivalent base.
This example is an rhombohedron:
|
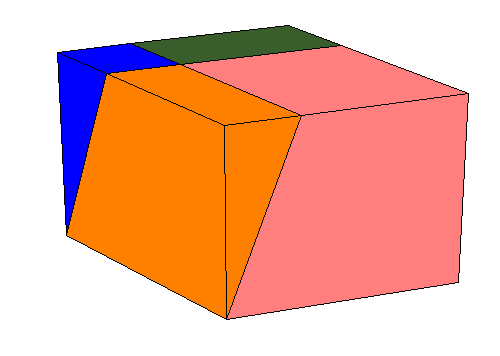
|
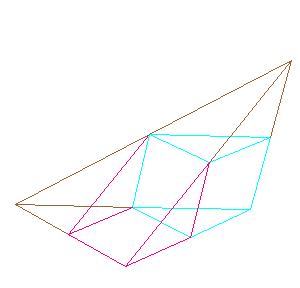
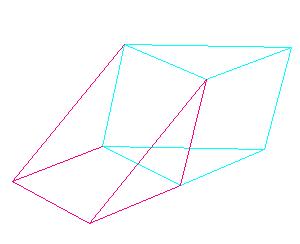
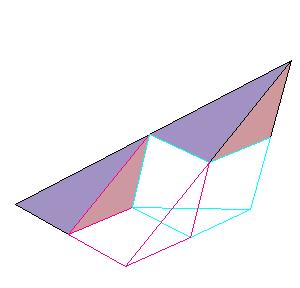
Book XII, Proposition 3.
Any pyramid with a triangular base is divided into two pyramids equal and similar to one another, similar
to the whole, and having triangular bases, and into two equal prisms, and the two prisms are greater than
half of the whole pyramid.
| 
| 
|
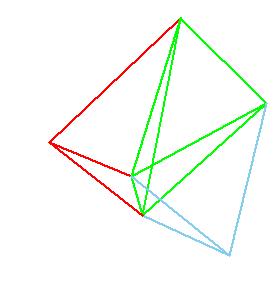
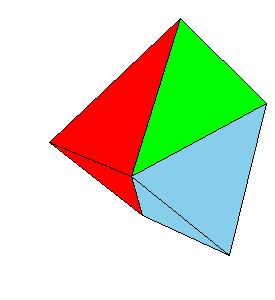
Proposition 7.
Any prism with a triangular base is divided into three pyramids equal to one another with triangular bases.
| 
|
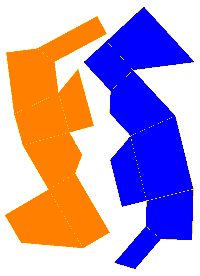
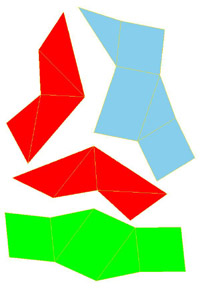
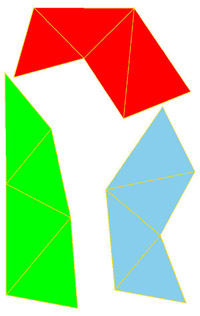
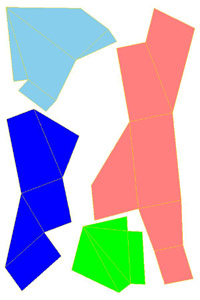
To make paper models use the following nets:

| 
| 
|
| 
| 
| 
|
References
[1] http://aleph0.clarku.edu/~djoyce/java/elements/elements.html
[2] Euclid's Elements, Part 3, Dover 1956
[3] Martin Kraus' Live3D applet http://www.vis.uni-stuttgart.de/~kraus/index.html
Dr. Izidor Hafner is a lecturer of mathematics in the Faculty of electrical engineering of the University of Ljubljana, Slovenia. He is a coauthor of 12 text books of elementary mathematics and logic. He made scientific contribution in the theory of von Neumann regular rings, logic ang geometry.