
| 
| 
|

| 
| 
|

| 
| 
|

| 
| 
|

| 
| 
|

| 
| 
|

| 
| 
|
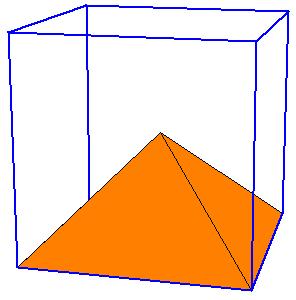
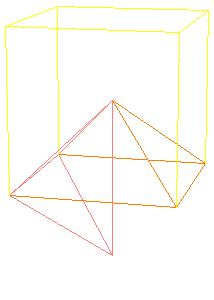
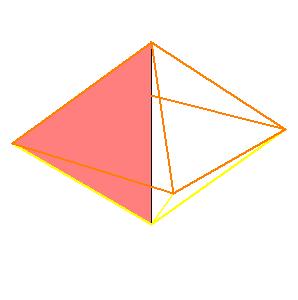
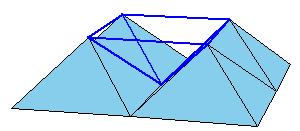
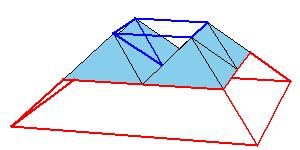
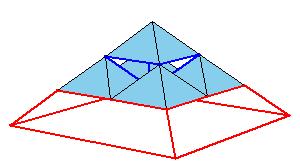
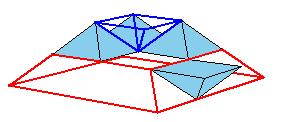
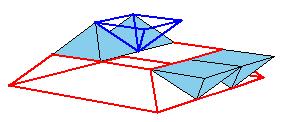
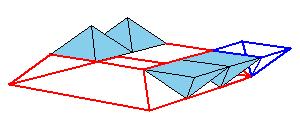
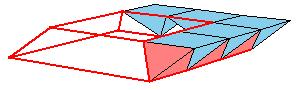
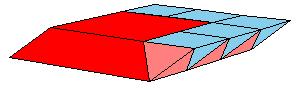
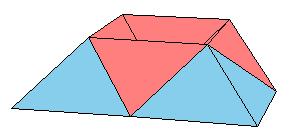
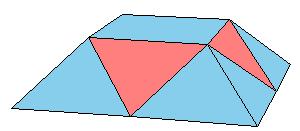
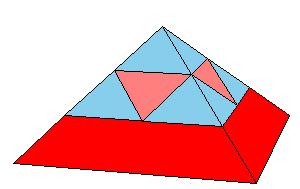
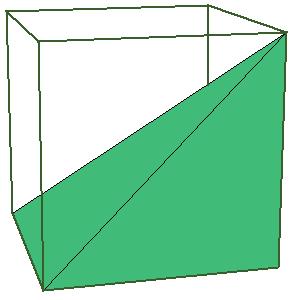
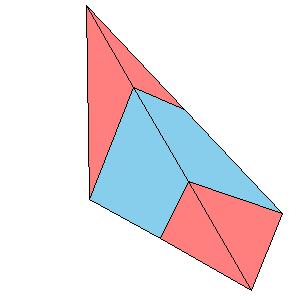
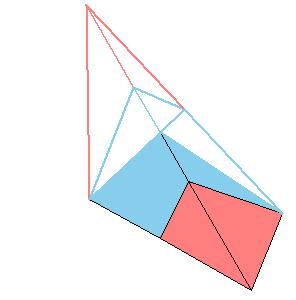
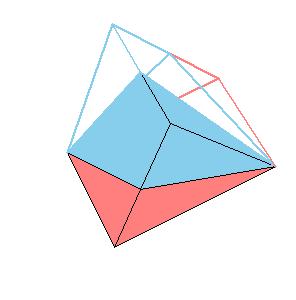
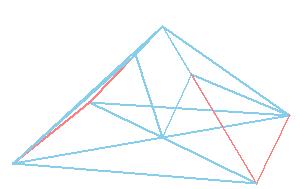
But there is a simpler dissection using only 4 pieces. We could cut the Juel's pyramid to 2 pieces
and reassemble them to Hill (or Sydler's Hill) tetrahedron [1, pg. 92, 2, pg. 234]. There is a 4-piece dissection
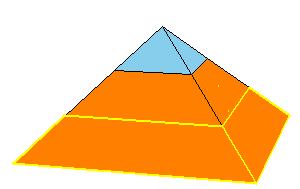
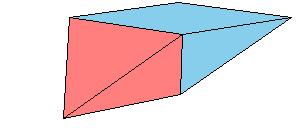
of the solid to a triangular prism obtained by Sydler [2, pg. 234].
But there is an even nicer hinged dissection of the tetrahedron to a different triangular prism, using construction found independently by P. Schobi and A. Hanegraaf [2, pg. 235]. This is a 3-piece dissection. This dissection yields a 4-piece dissection of Juel's pyramid to the prism.
| 
| 
|
| 
| 
|
| 
| 
|
| 
| 
|
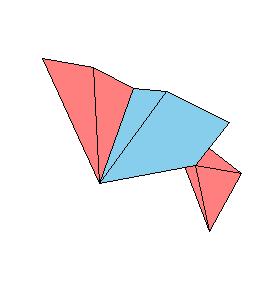
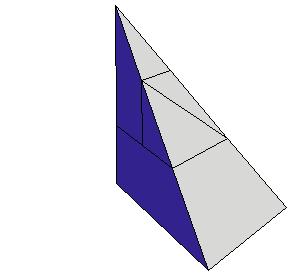
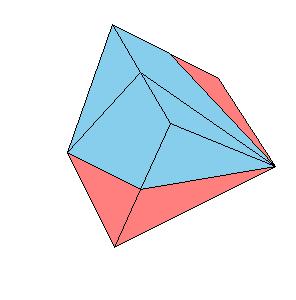
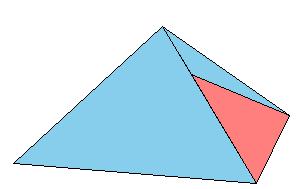
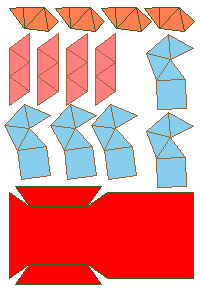
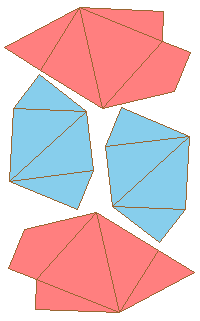
Make paper models using the following nets.
References
[1] V. G. Boltjanskii, Tretja problema Hilberta, Nauka, Moskva 1977.
[2] G. N. Frederickson, Dissections: Plane & Fancy, Cambridge U. Press, 1997.
[3] Martin Kraus' Live3D applet
[4] H. Meschowski, Grundlagen Der Euklidischen Geometrie (Croatian edition), Skolska Knjiga, Zagreb 1978