A dissection of two rhombic dodecahedra of the second kind to a cube



Izidor Hafner
Tomislav Zitko
Faculty of Electrical Engineering, University of Ljubljana
Trzaska 25 , 1000 Ljubljana , Slovenia
e-mail: izidor.hafner@fe.uni-lj.si

In [2] we found a symmetric dissection of 6 dodecahedra of the second kind and 8 prolate rhombohedra to a cube. The dissection is based on certain tilling of the space by these solids. In this article we based a dissection of 2 dodecahedra that uses 25 pieces. The dissection is based on space filling by rhombic dodecahedra of the second kind. Computation shows that the side length of the cube is identical with the length of the longer diagonal of the rhombus. To see a (LiveGraphics3D) animation dubleclick the picture.

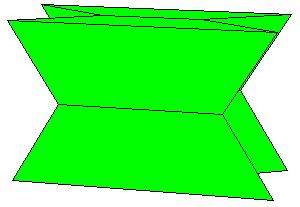
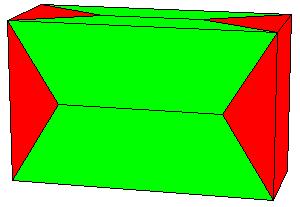
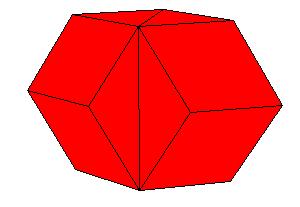
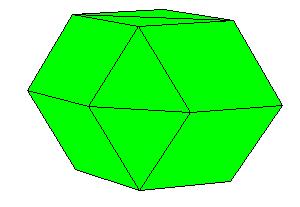
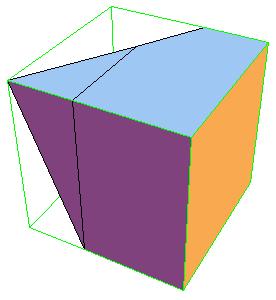
The obtained rectangular brick already has one appropriate dimension so we need only one P-slide to get a cube[1., pg.33].
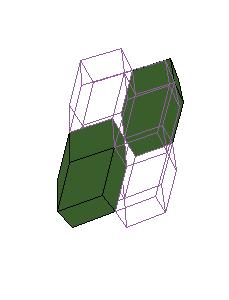
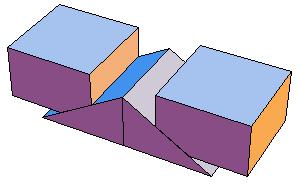
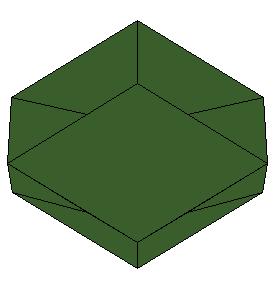
But we wish to get a symmetric dissection using one dodecahedron and eights of the other.
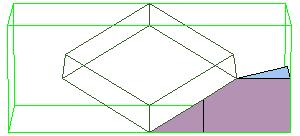
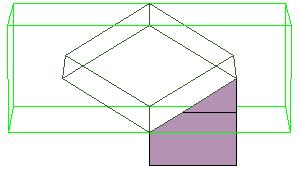
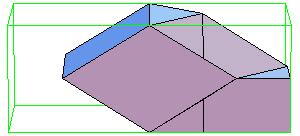
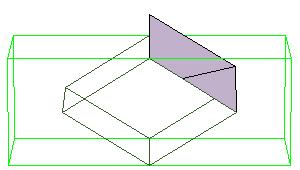
Essentially we repeat P-slide eight times.
Some of the intermediate steps are v given below.

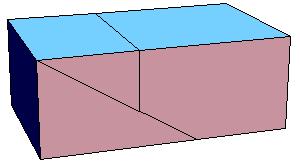
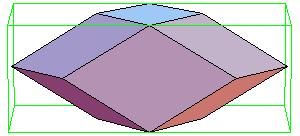
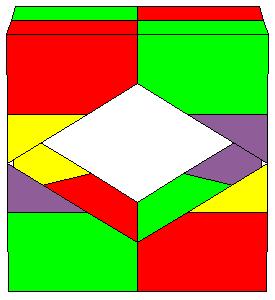
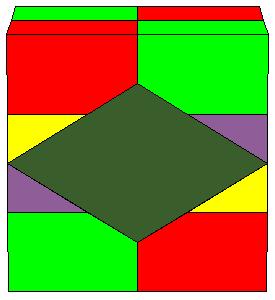
To make a paper model of a cube 2 copies of the following nets are needed together with a calibrated net of a rhombic prism.

References

[1] G. N. Frederickson, Dissections: Plane & Fancy, Cambridge U. Press, 1997,
[2] I. Hafner, T. Zitko, From dissection of the cube to space filling with prolate rhombohedra and rhombic dodecahedra of the second kind - published in Visual Mathematics Vol.4, No.2, 2002, 2, (5).