
There is a family of isohedral rhombic polyhedra that consists of prolate
and obtuse rhombohedron, (rhombic) dodecahedron of the second kind, discovered
by Bilinski in 1960, rhombic icosahedron, discovered by Fedorov in 1885 and
triacontahedron, discovered by
Kepler
in 1611 [1, p.156]. The faces of these
solids are congruent rhombs whose diagonals are in golden ratio. The last three
solids could be made by
gluing
appropriate number of rhombohedra. These five solids
are the only convex polyhedra of this kind. See Introduction to golden rhombic polyhedra.
The first three of the mentioned solids belong to so called five parallelohedra of
Fedorov and can fill the space [2, p.165].

| 
|
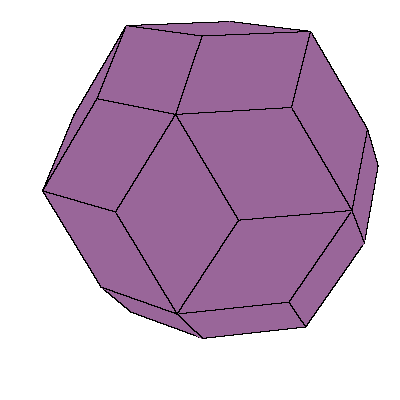
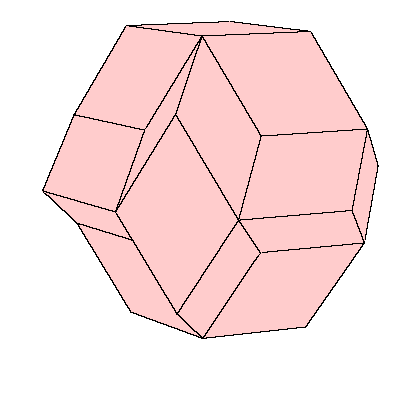
In [2, pgs.195, 196] an open aggregation by triacontahedra is given. The intestices
can be filled with a certain concave solid. The third figure below shows the solid
and on the right of it there is the complementary aggregation.
| 
|
| 
|
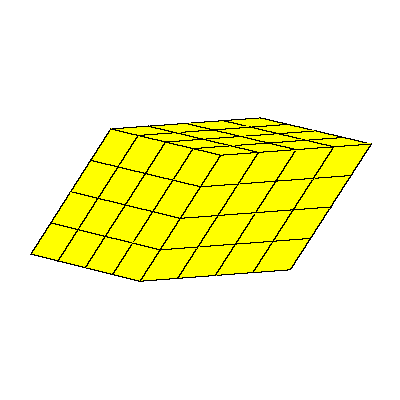
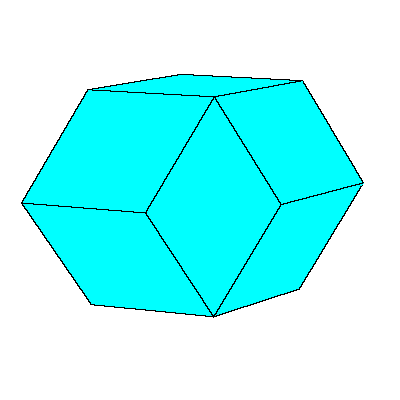
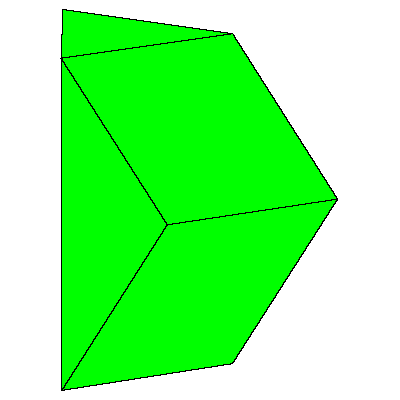
Our aim is to present an interesting filling of the space that uses prolate rhombohedron
and (rhombic) dodecahedron.
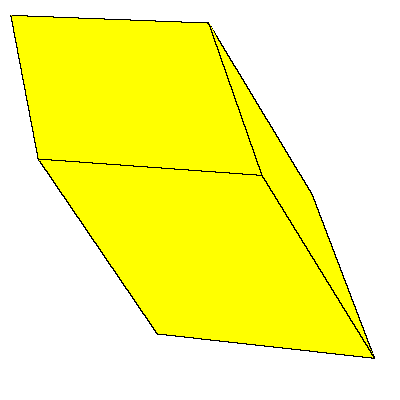
| 
|
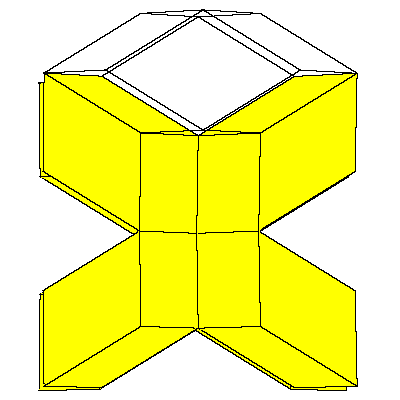
The crucial element in the construction will be the rhombic hexecontahedron. We can made
a model of it if we glue 20 prolate rhombohedra with common vertex. We remove 12 rhombohedra
in such way that the remaining solids form the cube. We can glue the dodecahedron to it
in such a way that exactly a quarter of it lies in the cube.
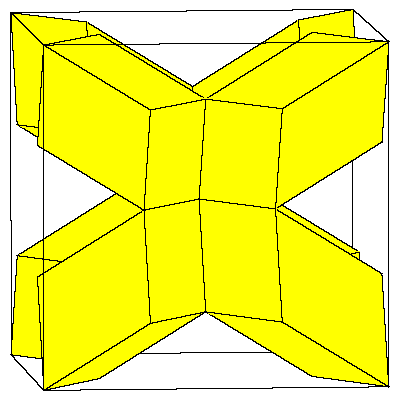
| 
|
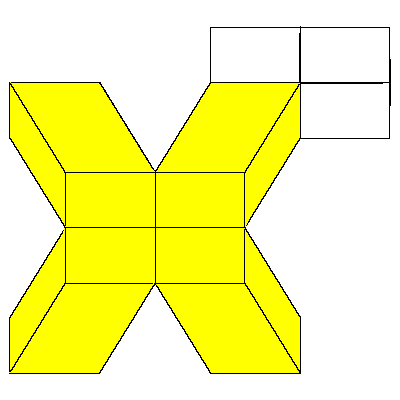
|
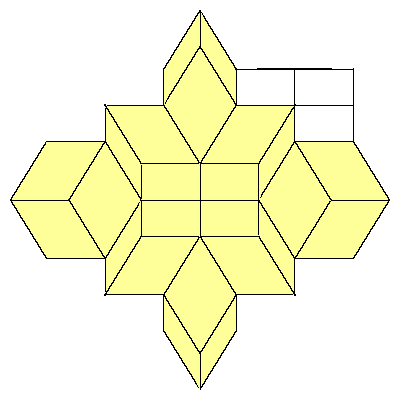
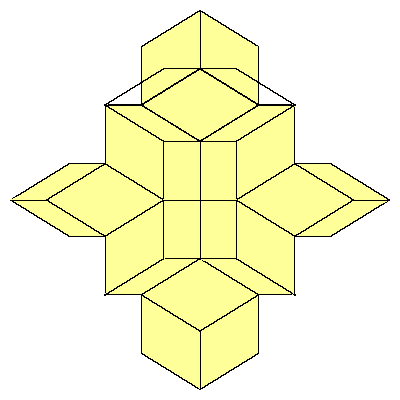
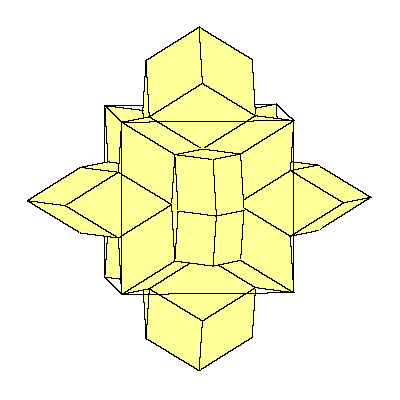
We could also replace 12 rhombohedra with 6 rhombic dodecahedra. Exact half of each
dodecahedron is inside the cube. If we look at the edges of the cube, we see that there
is a space for a quarter of the dodecahedron.
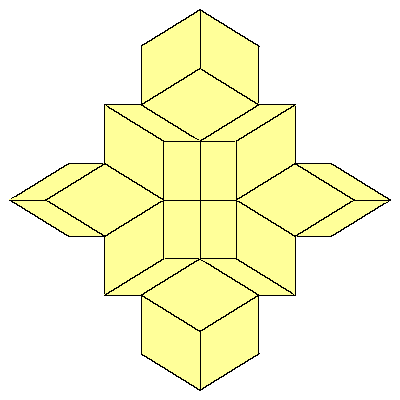
| 
|
| 
|
|
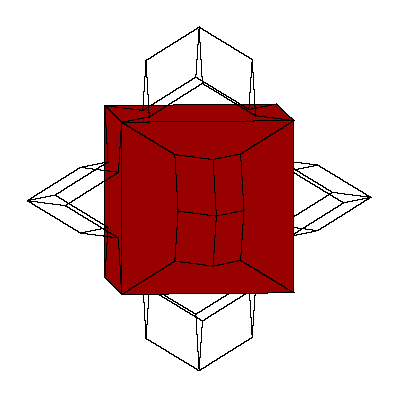
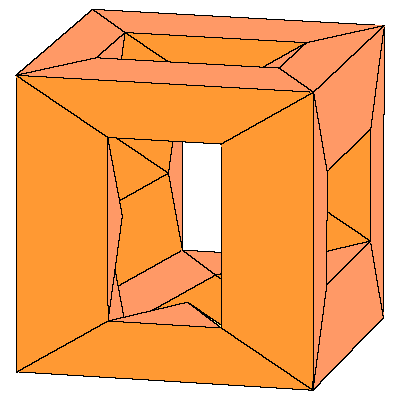
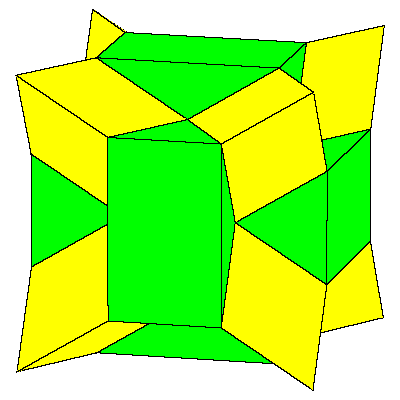
So the cube can be decomposed into 8 prolate rhombohedra, 12 quarters and 6 halfs of
the dodecahedron (so 6 dodecahedra all together).
| 
|
The above mentioned decomposition of the cube is given below.
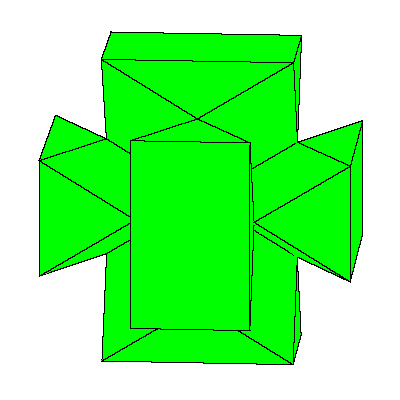
| 
|
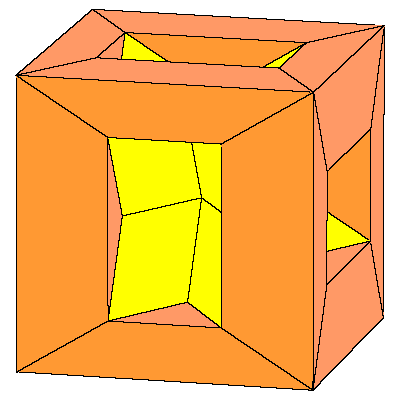
| 
|

|
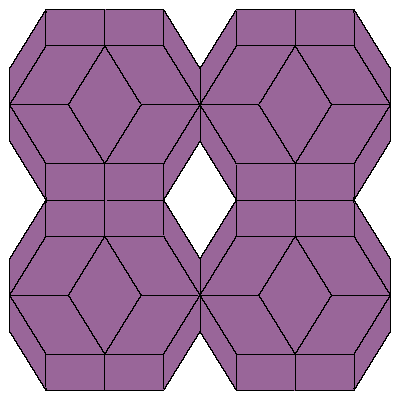
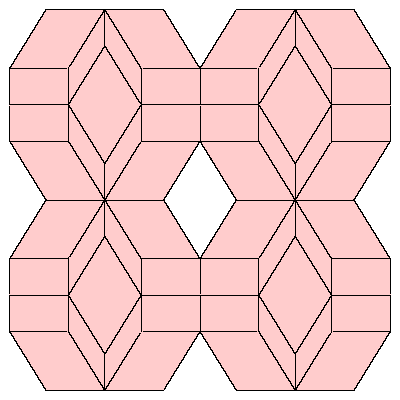
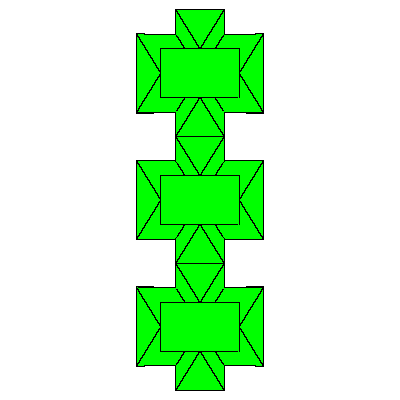
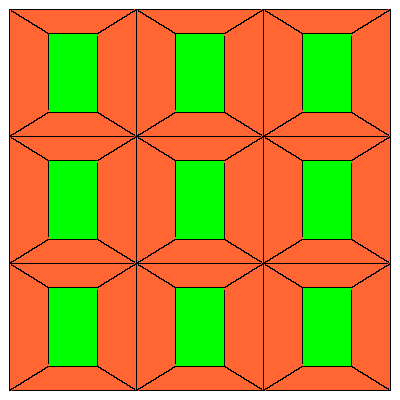
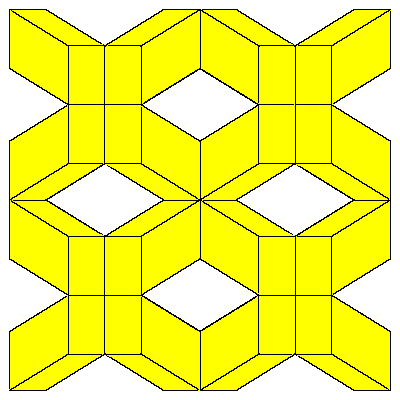
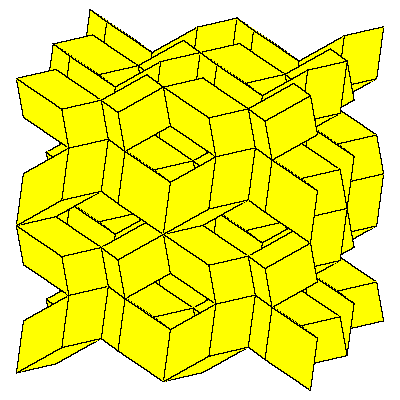
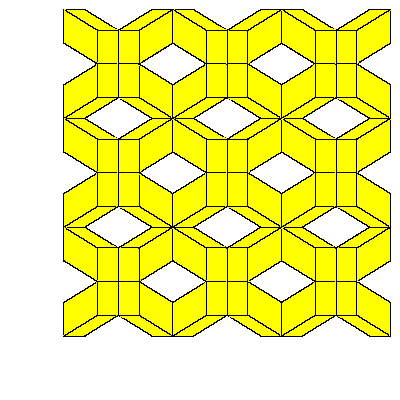
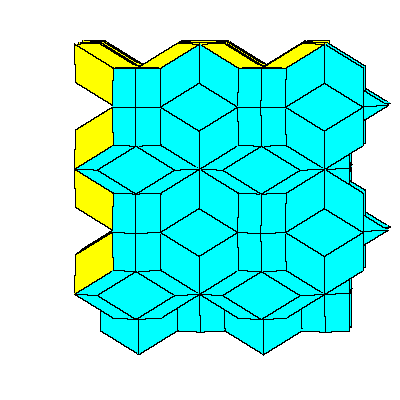
Figures below represent one layer of space filling.
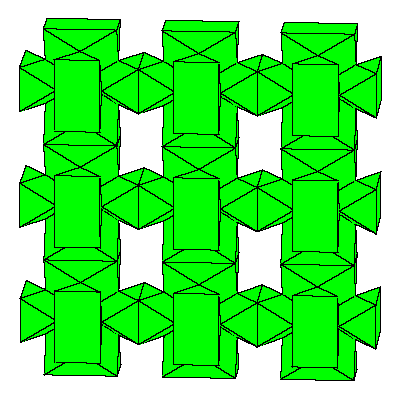
| 
|
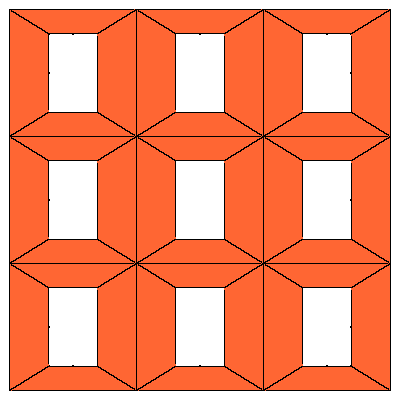
| 
|
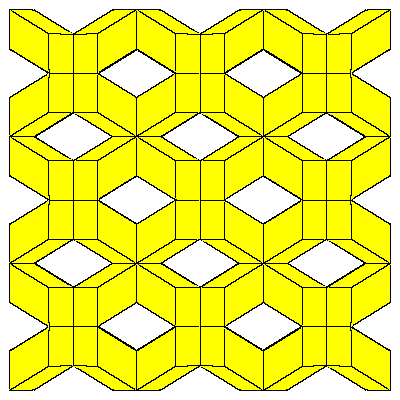
| 
|
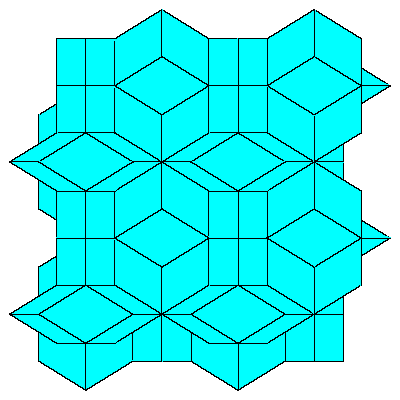
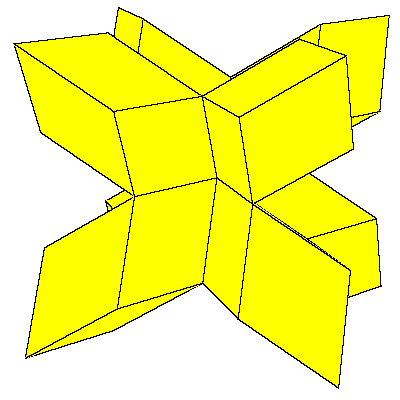
To fill the space we do not need to decompose dodecahedra. We only need to take 6 of them
in special combination.

| 
|
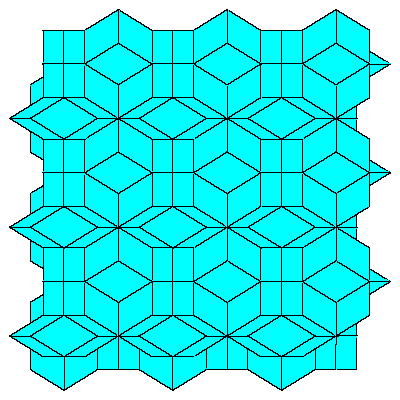
| 
|
| 
|
| 
|