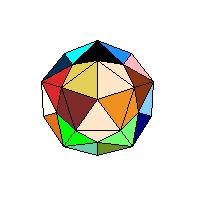
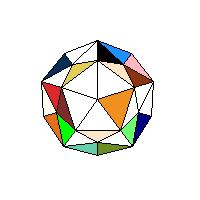
In the paper Colouring polyhedra and labyrinths on polyhedra, MiS, September 2001, pg. 9-10, we presented two types of problems on polyhedra nets. Such problems were used on National competition in recreational mathematics and were intended for gifted high school students. To test spatial abilities of an average student more basic type of problems should be used. For a polyhedron net this means that a student should indicate which sides of the net should be glued together to form the polyhedron. So the task is to present this well known problem in an attractive form. The problems shown bellow are also available as Java applets (Space Visualization Olympiad). A polyhedron net is a polygon whose sides should be glued in pairs to get an edge of the polyhedron. So the basic problem is to find all pairs of corresponding sides. Of course, at the same time we glue vertices of the polygon into vertices of the polyhedron. So the second problem is to indicate vertices that belong to the same solid vertex.
For the first problem the faces of a polyhedron are subdivided into isosceles triangles having edges as base lines and the centre as a vertex. Since each edge is the base of two triangles, both will be coloured with the same colour. So the number of colours equals the number of edges. On the net only one triangle of each pair will be coloured. The task is to colour the other triangle.
We are giving two examples of this problem, one on a dodecahedron and one on the rhombic icosahedron (to start LiveGraphics3D animation click an illustration).
Now we are interested in vertices. Each vertex belongs to three or more faces of a polyhedron. The faces are subdivided into quadrilaterals that join a vertex, the midpoints of adjacent edges and the centre of the face. The quadrilaterals belonging to the same vertex are colored with the same colour. On the net only one quadrilateral for each vertex is coloured. The task is to colour the others. We give examples of the problem on an icosahedron and on the rhombic dodecahedron.
Of course, initial colours are not necessary but they add some attraction to the problem. Let as take a dodecahedron as an example. Problems:
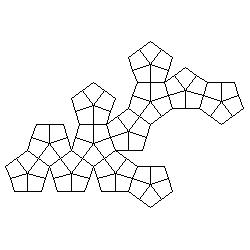
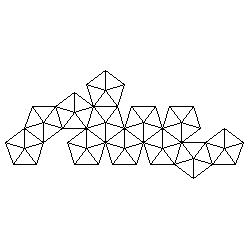
Solutions (colours are replaced by numbers):
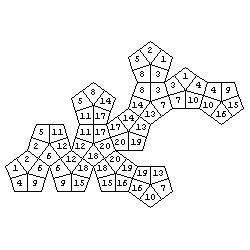
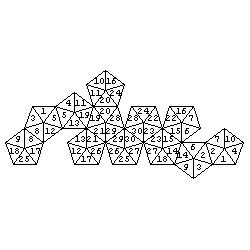
Here is a set of about one hundred problems (with solutions) of the above type.
[1] Hafner, I: Colouring polyhedra and Labyrinths an Polyhedra
, Mathematics in School, September 2001, Vol. 30,
No. 4, pgs.8-9
[2] http://Olympiad.fe.uni-lj.si
[3] Hafner I., Zitko T.: Colouring Platonic Solids, submitted