Introduction

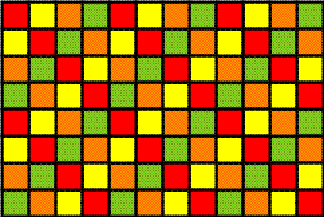
Figure 1 presents an example of a simple helix matrix of dimensions 8×12. Its matrix elements are 0, 1, 2, or 5.

Figures 2a, b, c and d illustrate the distribution of the 2’s, 0’s, 1’s, and 5’s, respectively.

Distribution of 2’s (a)	Distribution of 0’s (b)
Distribution of 1’s (c)	Distribution of 5’s (d)

Figure 3 presents the distribution of the four numerical values.

Imagine the matrix wrapped around a cylinder. We have four strings of eight 2’s and four parallel strings of 0’s. In the opposite direction, we have four strings of eight 1’s and four strings of eight 5’s. Imagine several of these cylinders piled up to form a tall cylinder. Now the (coloured) number strings circle around the tall cylinder as helices. Hence I will call this type of matrix a simple helix matrix. A simple helix matrix, because later on we will introduce more complex helix matrices. 
 
 

Simple helix matrices

Figure 4 presents the structure of a simple helix matrix of the same dimensions as the matrix in Figure 1. This structure is different from the structure in Figure 3. A helix matrix with a structure like in Figure 3, I will call a positive helix matrix. A helix matrix with a structure like in Figure 4, I will call a negative helix matrix.

We may define positive and negative simple helix matrices as follows.

A matrix A of dimensions (2m)×(2n) will be called a positive simple helix matrix, if the following conditions hold simultaneously:

Theorem 1: The number of helices (strings of equal numbers) of an either positive or negative simple helix matrix of dimensions (2m)×(2n) is equal to the greatest common divisor of 2m and 2n.

The situation of a simple helix matrix that is positive and negative at the same time is a little bit different. Figure 5 presents an example. The two numbers alternate as the checkers of a chessboard. The number of helix strings of equal numbers of such a special simple helix matrix is twice the greatest common divisor of 2m and 2n.

Multiplication of simple helix matrices

Figure 6 displays the multiplication of the positive simple helix matrices A and B of dimensions 8×12 and 12×4, respectively. The resulting matrix AB is also a positive simple helix matrix.

Figure 7 presents the multiplication of several positive and negative simple helix matrices of dimensions 6×6.

This experimentation leads to the formulation of the conjecture that the multiplication table of positive and negative simple helix matrices is similar to the multiplication table of positive and negative numbers (Figure 8). The reader is invited to prove the corresponding theorem.

Theorem 2: The multiplication table of positive and negative simple helix matrices is analogue to the multiplication table of positive and negative numbers:

The same multiplication table is valid for cycle matrices too (cf. Gerdes, 2002a). Like in the case of cycle matrices of period p, let us see if it is possible to introduce helix matrices of period p.
 
 

Helix matrices of period p

Let us consider a 8×12 matrix. For this matrix to be a positive simple helix matrix, all matrix elements on the equally coloured unit squares of Figure 3 should be equal. For instance, all matrix elements on the red unit squares (Figure 2a) should be equal. If these matrix elements were not equal but alternately 2 and 4, the respective helix would look like Figure 9.

We may say that this helix has period 2. If all helices have period 2, like in the example in Figure 10, we may call the matrix a helix matrix of period 2.

Observing well matrix P in Figure 10 we see that its negative helices have also period 2 (see the example in Figure 11). In other words, P is both a positive and a negative helix matrix of period 2.

Figure 12 presents an example of a helix matrix of dimensions 6×4. Both its positive and its negative helices have period 3. 

The number 3 is a divisor of one of the dimensions of the matrix. We may call the matrix a helix matrix of period 3. The examples suggest that it is not possible to distinguish between positive and negative helix matrices of period 2, 3, …

In general, we may characterise helix matrices of period p as follows. A matrix of dimensions (2m)×(2n) is called a helix matrix of period p if all its helices have period p.

Figure 13 presents examples of the multiplication of helix matrices of period p.

In each case, the product matrix AB is a helix matrix of the same period as the helix matrices A and B. 

It may happen, however, that the period p is not a divisor of the dimensions of the product matrix, as in the example in Figure 14.

All helices of the product matrix AB of dimensions 4×4 are constant. In other words, they have period 1. Having period 1, they have automatically any period, including period 3.

On the basis of our experimentation, the following theorem may be conjectured. The reader is invited to prove it.

Theorem 3: The product of two helix matrices of period p is a helix matrix of period p.

We may note that the class of simple helix matrices that are simultaneously positive and negative is the same as the class of helix matrices of period 1.
 
 

Concluding remark

Cycle and helix matrices may appear as products of cylinder matrices, as will be shown in (Gerdes, 2002b).
 

References

Gerdes, Paulus (2002a), From Liki-designs to cycle matrices, Visual Mathematics, Vol. 7, March 2002 (http://members.tripod.com/vismath7/gerd/)

Gerdes, Paulus (2002b), Cylinder matrices ((http://members.tripod.com/vismath8/gerdcyl/cyl1.htm