|
Paulus Gerdes pgerdes@virconn.com
Introduction Figure
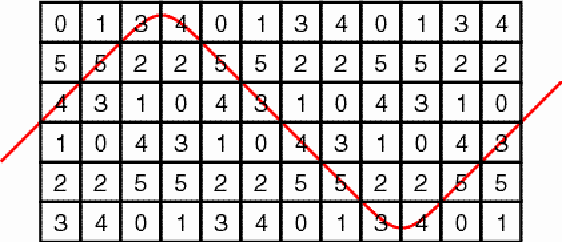
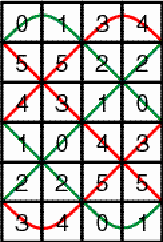
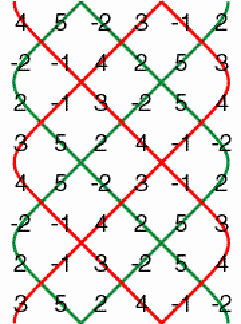
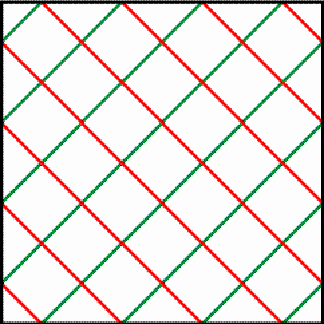
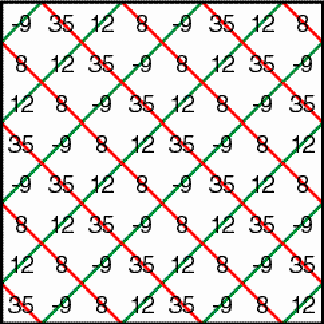
1 presents an example of a horizontal cylinder matrix of dimensions
6×4. Its six matrix elements are 0, 1, 2, 3, 4, and 5.
Example of a horizontal cylinder matrix Figure 1 The particular structure of the matrix may be understood if we join horizontally several copies of it. The numbers 4, 5, and 3 are recurring along a horizontal zigzag line (Figure 2).
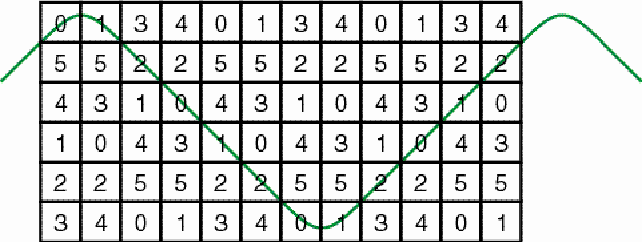
Figure 2 Likewise the numbers 0, 1, and 2 are recurring along another horizontal zigzag line (Figure 3).
Figure 3 Imagine the matrix
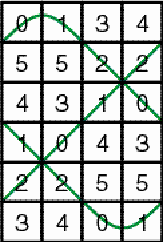
wrapped around a cylinder. Each horizontal zigzag line becomes a closed
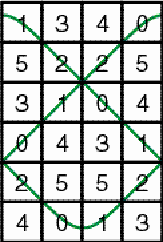
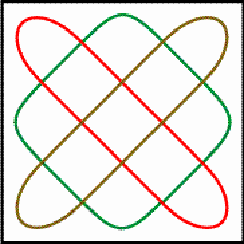
loop. Figure 4 presents the flat image of these loops.
The matrix is composed of two loops. Each loop has period 3. The matrix
will be called a horizontal cylinder matrix of period 3.
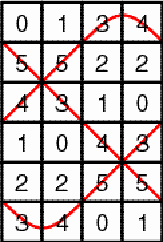
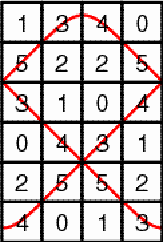
Figure 4 The matrix in Figure 5 is slightly different from the matrix in Figure 1: The first column of the matrix in Figure 1 became the last column in the matrix in Figure 5.
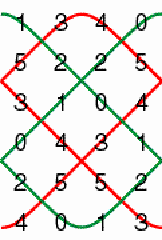
Figure 5 Figure 6 presents the loops of the new matrix. Each loop continues to have period 3, but their position is displaced by one unitsquare.
Figure 6 To distinguish the two possible positions, we will call the matrix in Figure 1 a negative horizontal 6×4 cylinder matrix of period 3, and the matrix in Figure 5 a positive horizontal 6×4 cylinder matrix of period 3. The choice of the terms "negative" and "positive" will be justified by the analysis of the properties of the multiplication of cylinder matrices. Figure
7 presents an example of a positive vertical cylinder matrix of period
3. A vertical cylinder matrix is the transpose of a horizontal cylinder
matrix.
Example of a positive vertical cylinder matrix of period 3 Figure 7
Horizontal zigzag loops Let A be a matrix of dimensions (2m)×(2n). The first positive, horizontal loop (L1) may be characterised as follows: (2) if aijÎL1, i+j even, i = 1, …, 2m-1, j = 1, …,2n-1, then a(i+1)(j+1)ÎL1, (3) if aijÎL1, i+j odd, i = 2,…,2m, j = 1,…,2n-1, then a(i-1)(j+1)ÎL1, (4) if a(2m)(j)ÎL1, j even, j = 2,…,2n-2, then a(2m)(j+1)ÎL1, (5) if a1jÎL1, j even, j = 2,…, 2n-2, then a(1)(j+1)ÎL1, (6) if a(i)(2n)ÎL1, i even, i = 2,.., 2m-2, then a(i+1)(1)ÎL1, (7) if a(i)(2n)ÎL1, i odd, i = 3,…, 2m-1, then a(i-1)(1)ÎL1, (8) if a(2m)(2n)ÎL1, then a(2m)(1) ÎL1. The following theorem about the number of different negative, horizontal loops may be proven: Theorem 1: The number of negative, horizontal loops of a matrix of dimensions (2m)×(2n) is equal to the greatest common divisor of 2m and n. The same holds for
the number of positive, horizontal loops.
Cylinder matrices of period p A matrix of dimensions (2m)×(2n) will be called a positive, horizontal cylinder matrix of period p if all its positive horizontal loops have period p. Negative horizontal, positive vertical and negative vertical cylinder matrices of period p may be defined analogously. The number of matrix
elements in each loop should be a multiple of p. As the total number
of loops is gcd(2m,n) and the total number of matrix
elements is 4mn, it follows that p has to be a divisor of
4mn/[gcd(2m,n)].
Multiplication of horizontal cylinder matrices Figure 8 presents examples of the multiplication of horizontal cylinder matrices of dimensions 6×4 and dimensions 4×12. The product matrices of dimensions 6×12 are composed of six loops. Like the multiplicands, the product matrices have period 3.
(a)
(b)
(c)
(d) Figure 8 In agreement with what the examples suggest, the following theorem may be proven: Theorem
2: The multiplication table of positive and negative horizontal
cylinder matrices of period p is analogue to the multiplication
table of positive and negative numbers (Figure 9).
Multiplication table of horizontal cylinder matrices Figure 9 Transposition of the horizontal cylinder matrices leads immediately to Theorem 3. Theorem 3: The multiplication table of positive and negative vertical cylinder matrices of period p is analogue to the multiplication table of positive and negative numbers. What may be said about the multiplication of horizontal
and vertical cylinder matrices?
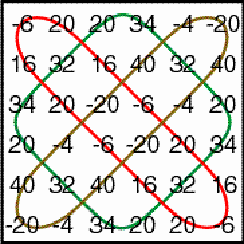
Multiplication of horizontal and vertical cylinder matrices Figure 10 presents the negative, horizontal cylinder matrix P and the negative, vertical cylinder matrix Q. Both matrices have period 3.
Figure 10 As their dimensions
are 6×8 and 8×6 respectively we can calculate both PQ
and QP. Figure 11 presents PQ and QP.
Figure 11 The matrix PQ is a positive cycle matrix of period 3 (cf. Gerdes, 2002a) (see Figure 12a, b), whereas the matrix QP is a positive simple helix matrix (cf. Gerdes, 2002b) (see Figure 12c, d).
Figure 12 Figures 13, 14, and 15 present further examples of the multiplication of horizontal cylinder matrices and vertical cylinder matrices of period 3. Each time horizontal times vertical leads to cycle matrices and vertical times horizontal leads to simple helix matrices. The product matrices are positive if both cylinder matrices have the same sign; the product matrices are negative if the two cylinder matrices have opposite signs.
Figure 13
Figure 14
Figure 15 Figure 16 presents the multiplication table for horizontal and vertical cylinder matrices as may be conjectured on the basis of the experimentation.
Multiplication table of horizontal and vertical cylinder matrices Figure 16
The following conjectures may be formulated: Conjecture 4: The products of horizontal and vertical cylinder matrices of dimensions (2m)×(2n) and (2n)×(2m), respectively, that have the same period p, are cycle matrices of period p. The cycle matrix is positive if both cylinder matrices have the same sign; the cycle matrix is negative if the cylinder matrices have opposite signs. In Gerdes (2002a) only square cycle matrices are defined. The concept of cycle matrix may be extended to non-square matrices. For instance, the matrix in Figure 17 may be considered a positive 6×12 cycle matrix of period 3. It appears as the product of the horizontal and vertical cylinder matrices of period 3 in Figure 18.
Figure 17
Figure 18 Conjecture 5: The products of vertical and horizontal cylinder matrices of dimensions (2m)×(2n) and (2n)×(2s) respectively, that have the same period p, are single helix matrices. The simple helix matrix is positive if both cylinder matrices have the same sign and is negative if the two cylinder matrices have opposite signs.
Figure 19
Figure 20
For certain dimensions
and periods, cylinder matrices may be simultaneously positive and negative.
For instance, the horizontal and vertical matrices of dimensions 5×4
and 4×5 with period 5 presented in Figure 19 are
simultaneously positive and negative. Their product matrices AB
and BA (Figure 20) are also simultaneously positive
and negative. In the case of the helix matrices, this means that they are
helix matrices of period 1.
Multiplication of vertical cylinder matrices and cycle matrices Figure 21 presents examples of the multiplication of vertical cylinder matrices and cycle matrices. Extrapolation on the basis of these examples leads to the following conjecture: Conjecture 5: The product of a vertical cylinder matrix and a square cycle matrix having the same period p is a vertical cylinder matrix of period p. The sign of the product matrix is equal to the product of the signs of the multiplicands. The reader is invited to (im)prove the conjectures and to discover more properties of cylinder matrices.
(a)
(b)
(c)
(d) Figure 21
References Gerdes, Paulus (2002a), From Liki-designs to cycle matrices, Visual Mathematics, Vol. 7, March 2002 (http://members.tripod.com/vismath7/gerd/) Gerdes,
Paulus (2002b), Helix matrices, http://members.tripod.com/vismath8/gerdhel/hel.htm)
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||