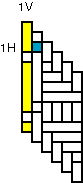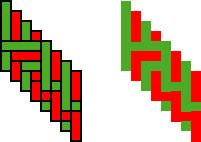|
Colour transformation of strip patterns in Tonga basketry (Mozambique) Paulus Gerdes Mozambican Ethnomathematics Research Centre, C.P. 915,
Abstract The paper analyses the recent and rare phenomenon
of the colour transformation of plaited strip patterns on Tonga baskets
by the use of alternating colours in both weaving directions. To weave
such a strip the basket weaver has to think and work in function of the
original strip pattern in order to achieve the new pattern. Being influenced
by the new pattern would complicate the execution of the weaving.
Gitonga is the main language of the population living in the districts around the Inhambane bay in Southeast Mozambique. About 170,000 people have Gitonga as their mother tongue. Because of their beauty and utility, twill-plaited baskets made by Tonga weavers, mostly women, are among the most appreciated products of Mozambican craft. Baskets of the highest quality and with most variation are produced on the peninsula of Linga-Linga, almost only reachable by boat. The peninsula lies in the district of Morrumbene, about 500 km to the Northeast of the country’s capital Maputo. Some baskets are commercialised at nearby markets and others, like the ones to be analysed below, find their way directly to the markets of Maputo. The paper presents an apparently recent phenomenon in
Tonga basket weaving. It analyses a type of colour transformation of plaited
strip patterns.
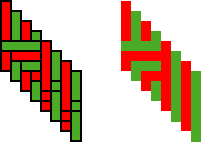
New horizons in Tonga basketry Tonga basket weavers are creatively exploring new horizons. Whereas in (Gerdes & Bulafo 1994) I reported 96 different strip patterns observed on Tonga handbags called gipatsi (Plural: sipatsi), eight years later it was possible to produce a catalogue of 362 distinct strip patterns (Gerdes 2003). Photograph 1 presents an example of a gipatsi. To produce these handbags the artisans use as basic weave the 2/2 twill. By introducing some systematic changes along bands of the texture, they create the strip patterns (for an introduction see Gerdes 1998, chapter 1 or Gerdes 1999, pp. 87, 140-143). In the months following the conclusion of the manuscript of (Gerdes 2003) I observed 32 more strip patterns. Figure 1 presents the visual images of some of these recently observed new strip patterns. Some new phenomena in Tonga basket weaving are almost
ephemeral. Suddenly they appear as the result of imaginative experimentation,
and then they may be improved, adapted or abandoned for one reason or another.
For instance, in October 1999 I saw for the first time a hat decorated
with strip patterns of the type that are visible on sipatsi handbags
(see Photograph 2). Only in February 2001 I saw another
hats with strip patterns. Another new and very rare phenomenon is the ‘colour
transformation of strip patterns.’ So far observed I observed it only in
February, March and August 2001. Since then more then a year passed and
I have not seen any more instances of this phenomenon.
Transforming strip patterns (see Gerdes 2003, pp. 146-152) Photograph 3 presents a gipatsi handbag. A horizontal band breaks the plane pattern of vertical zigzags. Photograph 4 presents a close-up of the band. Photograph 5 presents another handbag acquired on the same day (February 17, 2001) and at the same stand at Maputo’s central market. Another band interrupts the plane pattern of vertical zigzags. Photograph 6 presents a close-up. Normally when a gipatsi is woven all strands in one direction are coloured while the others maintain their natural colour. In the figures and photographs coloured strands are the strands that go upward from the right to the left. In the case of the handbags in Photographs 3 and 5 the situation is completely different. In both weaving directions artificially coloured strands and natural-coloured strands alternate, producing the basic plane pattern of vertical zigzags (see Gerdes 2003 on plane patterns in Tonga basketry). Now, let us see how we may understand the appearance of the exceptional horizontal bands. Figure 2 presents the weaving structure and the visual image of a normal gipatsi strip pattern. When alternating artificially coloured strands with natural-coloured strands in both weaving directions the colouring of the weaving structure in Figure 2a is transformed. It may lead to the plaited pattern in Figure 3a. Figure 3b presents the resulting visual image. This visual image corresponds to the band in Photograph 4. In the same way, Figures 4 and 5 display the colour transformation of a normal gipatsi strip pattern into the band of Photograph 6. When the inventor of the colour transformation executes for the first time the transformation of a certain gipatsi strip pattern in mind, most probably the basket weaver cannot imagine the final result. The inventor has the difficult task to try to forget about the colours of the strands and try to weave colour-blind, just acting in terms of the weaving structure. Once concluded several copies of the motif, the basket maker may try to use the new visual image as orientation. Photograph 7 shows a handbag where
only in one weaving direction the colour transformation has been executed.
Figure 6 presents the underlying original strip pattern, the new colouring
of its weaving structure and the visual image of the final strip pattern.
Periodicity Figure 7 presents the gipatsi motif No. 133 in our catalogue (Gerdes 2002, p. 50). It has as period the odd number 7. This implies that if in both weaving directions alternating colours are used, the design will repeat itself after 14 strands. In other words, the period changes to 14, as Figure 8 shows. Photograph 8 presents a handbag where this colour transformation has been realised. Photograph 9 presents the result of
the colour transformation of a strip pattern with gipatsi motif
No. 151 (Gerdes 2002, p. 54). Figure 9 displays the original
strip pattern, its visual image, the new colouring of its weaving structure
and the visual image of the resulting strip pattern. The original pattern
has period 7, whereas its colour transformation has period 14. Not only
the period changed, also its symmetry.
Symmetry One may notice that the visual images of the original
strip pattern and the resulting strip pattern (may) have different symmetries.
For instance, in the last example, the visual image of the transformed
pattern lost the bilateral symmetry of the visual image of the original
pattern and gained a two-colour symmetry that the original pattern did
not have.
Transformation of couples of strip patterns On August 9, 2001 I came across two sipatsi with intriguing designs (see Photographs 10 and 11). Are we dealing with the ‘fanciful’ creation of completely new patterns? Or are they new variations within the context of the cultural tradition? Does some ‘secret’ lie behind their invention? Consider the gipatsi motif in Figure 10. It is motif No. 117 in our catalogue (Gerdes 2002, p. 46). Its dimensions are 6×11. Let us analyse how the image of this motif may change when alternating colours p and q are used in both weaving directions. The first vertical strand at the left (see 1V in Figure 11) can be coloured either p or q, likewise the first horizontal strand (see 1H in Figure 11) can be coloured either p or q. Four possibilities result for the colour transformation of the initial motif. They are [p, p], [p, q], [q, p] and [q, q], where [m, n] denotes the alternating colouring whereby the first vertical strand has colour m and the first horizontal strand has colour n. Figure 12 displays the four possibilities in the case of the considered motif. The visual image of the possibilities [p, p] and [q, q] is rather similar in the sense that the designs as such are equal, only the colours are reversed. In the same way, the possibilities [p, q] and [q, p] lead to designs of which the colours are reversed (Figure 13). Figure 14 presents the visual image of the three strip patterns obtained by using the gipatsi motif in Figure 10. The first image corresponds to the ‘normal’ weaving with different colours in both weaving directions, whereas the second and third correspond to the possibilities [p, p] and [p, q] of using alternating colours in both weaving directions. Let us imagine now that a weaver likes to repeat on the bag two bands with the same motif. For instance, the weaver opts to introduce a copy of the motif below another one separated by three rows of normal 2/2 weaving (see Figure 15a). Figure 15b shows the image of the double motif unit if the normal weaving with different colours in both weaving directions is used. If however alternating colours are used in both directions, what will the image look like? If the upper copy of the motif is transformed according to the possibility [q, p], what will happen with the lower copy of the motif? The distance between the top of the first copy and the top of the second copy of the motif is equal to the height of the motif (=11) plus the height of the three rows of 2/2 weaving (= 3×2 = 6). As this distance is equal to the odd number 17, the colours in the horizontal direction are reversed. In other words, the lower copy is transformed according to the alternating colouring [q, q]. Figure 16 presents the image of the double motif unit if alternating colouring is used in both weaving directions. Figures 17 and 18 present the image of the two bands if normal and alternating colourings are used. The image in Figure 18 corresponds to the handbag in Photograph 10. The secret of its apparently fanciful design is revealed: the weaver repeated a well-known motif transforming by using alternating colours. The motifs in the two bands become dissimilar as in one of the weaving directions they have opposed colours whereas in the other directions they have the same colours. In order to execute the alternating colouring transformation, the weaver has to concentrate completely on the weaving structure avoiding to be distracted anyhow by the colours. Let us now try to unveil the secret behind the designs in Photograph 11. Consider the gipatsi motif in Figure 19. It is motif No. 165 in our catalogue (Gerdes 2002, p. 56). Its dimensions are 8×7. Figure 20 presents its [q, q] and [p, q] transformations. Figure 21 presents the visual image of the three strip patterns obtained by using the gipatsi motif in Figure 19. The first image corresponds to the ‘normal’ weaving with different colours in both weaving directions, whereas the second and third correspond to the possibilities [q, q] and [p, q] of using alternating colours in both weaving directions. Once again let us imagine that the weaver likes to repeat two bands with this motif. The weaver may opt to introduce a copy of the motif below another one separated by three rows of normal 2/2 weaving and displace it one unit to the left and one unit upwards (see Figure 22). In this way corresponding parts of the motif undergo a vertical displacement of 7+6-1 = 12 strands and a horizontal displacement of one strand. What will happen with the two copies when alternating colouring is used? If the top copy of the motif is transformed according to [q, q], then the bottom copy will be transformed according to [p, q] (see Figure 23). Figure 24 displays the image of the two bands in the cases where the normal colouring and the alternating colouring are used. The image of the second one corresponds to the handbag in Photograph 11. The creativity of the basket weaver manifests itself in the combination of weaving the structure of repeating ‘normal’ strip patterns and of the simultaneous use of alternate colours in both weaving directions. Let me present a last example. Photograph
12 displays a large handbag. Photograph 13 presents
a close-up. Figure 25a shows the underlying, original
strip pattern and Figures 25b and c
its transformation and visual image.
Concluding remarks The invention of the colour transformation seems to be
recent. The transformation associates the experience of making sipatsi
with the idea of using alternating colours in both directions. The initial
execution of the idea is not easy. It demands high concentration and ability
on the part of the basket weaver. The reproduction of the new strip patterns
may become easier with their gradual mental fixation. However, as the resulting
strip patterns may be less appreciated then the original strip patterns,
either by the basket weaver(s), or by the artisan’s direct cultural environment
or by potential buyers, the incentive to continue with the discussed colour
transformation may not be strong for the basket weaver.
(a)
(b)
(c)
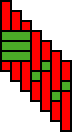
(d) Examples of sipatsi strip patterns Figure 1
(a)
(b) Weaving texture and visual image of a gipatsi strip pattern Figure 2
(a)
(b) Plaiting pattern and visual image after the colour transformation Figure 3
(a)
(b) Weaving texture and visual image of a gipatsi strip pattern Figure 4
(a)
(b) Plaiting pattern and visual image after the colour transformation Figure 5
(a)
(b)
(c) Underlying strip pattern, new colouring and visual image Figure 6
(a)
(b) Vertical and diagonal position of the gipatsi motif Figure 7
(a)
(b)
(c) Duplication of odd period with colour transformation Figure 8
Original gipatsi strip pattern (a)
Visual image of original strip pattern (b)
New colouring of the weaving structure (c)
Visual image of the resulting strip pattern (d) Colour transformation Figure 9
Gipatsi motif Figure 10
The first strands in both directions Figure 11
The four possibilities of alternate colouring [p, p], [p, q], [q, p] and [q, q] Figure 12
Visual image of the four possibilities Figure 13
Original strip pattern (a)
[p, p] colouring (b)
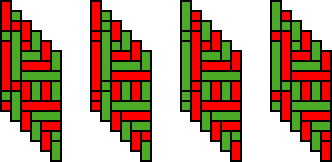
[p, q] colouring (c) Figure 14
Double motif unit Figure 15
Transformed double motif unit Figure 16
Normal colouring Figure 17
(a)
(b) Alternating colouring Figure 18
Gipatsi motif Figure 19
[q, q] colour transformation (a)
[p, q] colour transformation (b) Figure 20
Normal strip pattern (a)
[q, q] transformed strip pattern (b)
[p, q] transformed strip pattern (c) Figure 21
Double motif unit Figure 22
Transformed double motif unit Figure 23
Visual image of the ‘normal’ double band (a)
Visual image of the transformed double band (b) Figure 24
Original strip pattern (a)
Transformed strip pattern (b)
Visual image of the transformed strip pattern (c) Figure 25 Photograph 1
Photograph 2
Photograph 3
Photograph 4
Photograph 5
Photograph 6
Photograph 7
Photograph 8
Photograph 9
Photograph 10
Photograph 11
Photograph 12
Photograph 13
References ___ (1999), Geometry from Africa: Mathematical and Educational Exploration, The Mathematical Association of America, Washington DC ___ (2003), Sipatsi: Cestaria e Geometria na Cultura Tonga de Inhambane, Moçambique Editora, Maputo Gerdes, Paulus and Bulafo, Gildo (1994),
Sipatsi: Technology, Art and Geometry in Inhambane, Universidade
Pedagógica, Maputo
|