|
Geometry and Symmetry of Mavuku
Baskets
Paulus Gerdes Mozambican Ethnomathematics Research Centre, C.P. 915,
Abstract The paper presents
an analysis of mavuku containers produced by Makhuwa basket weavers
in the Northeast of Mozambique. The containers consist of two twill woven
circular trays. The paper discusses the symmetries and the geometric structure
of the weaving designs. The know-how of the old master-weaver Mulaliha
from Rapale receives particular attention.
Introduction – Twill Basketry and Symmetry The mavuku baskets belong to the category of twill-plaited baskets. Twilling is a form of plaiting whereby the strands in one direction may go over or under more than one strand in the opposite direction; in other words, the weaving is not always "over one, under one". The 2/2 twill indicates the "over two, under two" weave (see Figure 1a). The 3/3 twill represents the "over three, under three" weave (see Figure 1b). In both cases diagonal zigzag lines are visible that make angles of 45 degrees with the (horizontal and vertical) weaving directions. When the regular, balanced twill is interrupted at certain places of the fabric, other designs may be visible. Beautiful collections of twill-plaited baskets are included in LaPlantz (1993) and Sentance (2001). In (Gerdes 1990) I suggest twill basketry as an interesting theme for research in ethnomathematics and symmetry (see also Gerdes 1990a, 2002d). In several studies I analyse symmetry-mathematical aspects of twill basketry. For instance, in (Gerdes & Bulafo 1994, Gerdes 2003a) I present strip patterns on bags woven by Tonga women (Southeast Mozambique), and in (Gerdes 2000a, 2004) I discuss the symmetry on twill-plaited mats made by Yombe women from the Lower Congo area (see also Gerdes 1999, pp.126-137). Twill-plaited octagons from around the world are analysed in (Gerdes 2002). Near to conclusion is a classification and a catalogue of various types of plane patterns which appear in twill basketry. My colleague Marcos Cherinda (2002) studies the use of a weaving board to explore twill-plaited patterns in the mathematics classroom. A particular interesting class of twill basketry is composed of circular trays, often used as winnowing baskets. In the book "The Circle and the Square" (Gerdes 2000) I present a comparative analysis of the production of these trays. Schematically they are made in the following way: a square plaited mat is fastened to a circular rim, whereby the outstanding strands are either cut off or interlaced with the rim. Generally, it is easier to fasten the square mat to the rim if its midlines are visible in one way or another. The visibility may be achieved by introducing certain designs into the mat. The designs have often symmetries. The book analyses several possibilities to make the midlines visible and gives illustrative examples from Africa, the Americas, Asia and Oceania. Later I had the opportunity to analyse a collection of circular trays from the Peruvian Amazon, leading to the elaboration of the book "Geometry and Basketry among the Bora" (Gerdes 2002a). It may be noted that Guss (1989) presents a beautiful gallery of circular trays from the Yekuana (Venezuela). At present I am finishing a book on Geometry and Basketry in the Makhuwa Culture. About three million people speak the Makhuwa language. They live mostly in the northern coastal province of Mozambique, called Nampula, and its neighbouring provinces Cabo Delgado, Niassa and Zambezia. Two chapters of the book deal with circular trays. One deals with a particular group of small trays called epadge (plural: ipadge) that present designs consisting of plaited spirals (see the example in Figure 2). The other chapter deals with mavuku baskets composed of two circular trays. The following paper is an abridged translation
of the chapter on mavuku baskets. Nowadays only a few basket weavers
produce mavuku. An old basket weaver called Mulaliha lives in the
area of Rapale, to the Northwest of the City of Nampula. He is a specialist
in the production of mavuku. Several of the mavuku to be
analysed in the paper were made by the master Mulaliha and his assistant-student.
I had the opportunity to analyse about one hundred mavuku. In the
period from 1999 to 2001, twenty
mavuku were acquired for the collection
of our Mozambican Ethnomathematics Research Centre. The paper presents
an analysis of the mavuku baskets in our collection.
Production and weaving structure Makhuwa basket weavers produce a type
of container, called nivuku (plural:
mavuku). It is used
to keep and transport food or valuable objects like jewellery. The basket
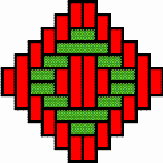
consists of two halves. Each half is a circular tray of a type called othokwa
(plural: ethokwa). One othokwa is the lid and the other is
the base of the container (see Photograph 1). The rims
of both lid and base are reinforced with strips of wood. An extra wooden
rim is sewn internally to the base so that it is easier to fit the lid,
as the diagram in Figure 3 illustrates. In most of
the cases the mavuku weavers use the 3/3 twill (see Figure
1b). Less frequent is the use of the 2/2 twill (see Figure
1a).
Discontinuity lines / Symmetry axes Often discontinuity lines break the basic weaving structure. They are symmetry axes. A discontinuity line marks the reversal of direction of the diagonal zigzag lines. The diagonals on the two sides of a discontinuity line are perpendicular. The discontinuity lines may be of two types, single or double. In the case of the 3/3 twill the strands go over 1, 3 and 5 strands, respectively, along a single discontinuity line (see Figure 4a) and over 2, 4, and 6 strands, respectively, along a double discontinuity line (see Figure 4b). Figure 5 presents the structure of both the lid and the base of a nivuku (diameter = 24,5 cm, height = 18,5 cm): it is characterised by one double discontinuity line. In the case of the 2/2 twill the jumps along a single discontinuity line are 1 and 3 (see Figure 6a) and along a double discontinuity line they are 2 and 4, respectively (see Figure 6b). Two or more parallel discontinuity lines appear in several mavuku. Two examples illustrate this situation. Figure 7 presents the weaving structure of the lid and the base of a nivuku (d = 24 cm, h = 18,5 cm, 3/3 twill). There are two double discontinuity lines, equidistant from the centre. The weaving design is divided into three bands and has rotational symmetry of 180 degrees. Figure 8 presents
the weaving structure of the lid and the base of another
nivuku
(d = 27 cm, h = 18 cm). This time there are three discontinuity
lines, dividing the texture into four bands. While the first and the third
discontinuity line are single, the central discontinuity line is double.
The design has axial symmetry.
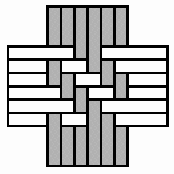
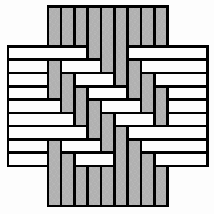
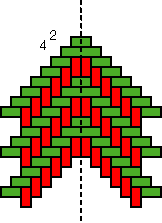
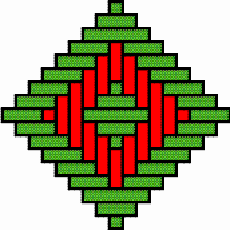
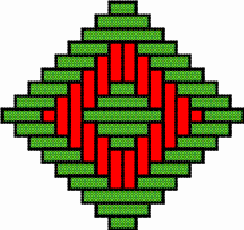
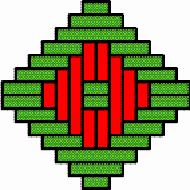
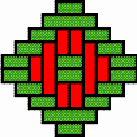
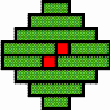
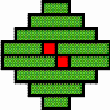
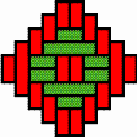
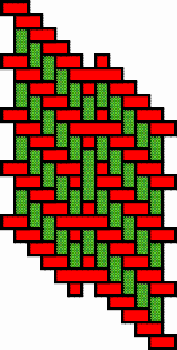
Structures of concentric toothed squares More frequently, the discontinuity lines constitute a cross, that divides the bottom of a half of a nivuku into four quadrants (Figure 9a), whereby a design of successive toothed squares around the centre of the texture appears (see the diagram in Figure 9b). The choice of the twill determines the possibilities for the shape of the centre of the texture. Figures 10 and 11 present the centre shapes observed on mavuku baskets. Figure 12 presents the weaving structure of the base of a nivuku (d = 27 cm, h = 20,5 cm) that has a centre of dimensions 6×5. The lid of the same nivuku has a 6×6 centre. Figure 13 presents the weaving structure of both lid and base of a nivuku (d = 24 cm, h = 17 cm), whereby the centre has dimensions 5×5. Around the centre there are two concentric toothed squares beyond which the initial symmetry is broken to form toothed lines in form of a P. In the case of two double discontinuity lines and an 8×8 centre, two interesting variants may be observed. They are symmetric to each other. The two central vertical strands go over one horizontal strand immediately before and after the horizontal axis, respectively. Figure 14 displays the two variants. The fabric obtains a rotational symmetry of 180 degrees. The variants seem to constitute a type of signature of the master-basket weaver Mulaliha and his student. So far I have not seen a similar centre structure elsewhere (see Gerdes 2000, 2002). An advantage of these variants consists of the fact that, in this way, one of the two central parallel strands never can glide upon the other under the lateral pressure of the other strands. Figure 15 presents the image of the lid of a nivuku that has the first variant as its centre. The base of the same nivuku has the second variant as its centre. Both variants presented in Figure 14 appear
in a very special basket, probably made by Mulaliha (see Photograph
2a). It is a container composed of two
mavuku (h = 33
cm, d = 24 cm). One might think that the double container consists
of two mavuku glued or sewn together, but this is not the case.
The inventor had a very original idea: the central parts of the base of
the upper nivuku and of the lid of the lower nivuku are woven
at the same time. The basket weaver realises the idea by plaiting with
pairs of strands, one on the top of another, instead of using single strands.
After concluding the central part of the square mat, he bends the outstanding
parts of the upper strands upwards, and he continues to weave them until
he finishes the mat to be fastened to the circular rim to constitute the
base of the upper nivuku. Next he bends the outstanding parts of
the lower strands downwards and he continues to weave until the lid of
the lower nivuku is completed. The base of the upper nivuku
and the lid of the lower nivuku are indissolubly interwoven (see
Photograph
2b). The basket weaver chose for both of them the structure of concentric
squares with the 8×8 centre. The two variants of Figure
14 were chosen for the lid of the upper nivuku and for the base
of the lower nivuku.
Figure 15 presents the
structure of the upper lid of the double container.
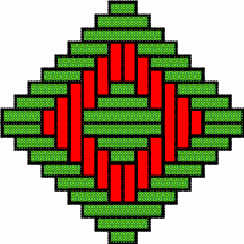
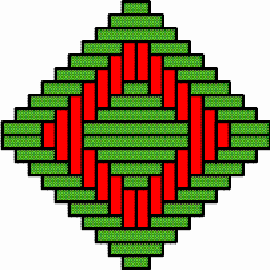
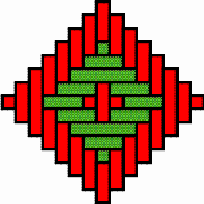
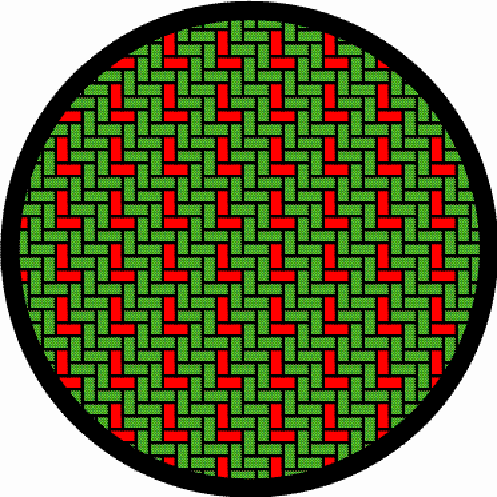
Multicentric structures It sometimes happens that the basket weaver opts for several discontinuity lines at the same time, producing a weaving structure of multiple centres. Figure 16 gives an example. It presents the structure of the lid of a nivuku (h = 17 cm, d = 24 cm). The twill is 3/3. The vertical diameter is the only vertical discontinuity line, while there are three horizontal discontinuity lines. The intersection of the vertical and the horizontal discontinuity lines produces three local centres, two in form of concentric squares (Figure 17) and one in form of an X (Figure 18). The structure of the base of the same nivuku corresponds to the one presented in Figure 15. Figures 19 and 20 present the weaving structure of the lid and the base of another beautiful nivuku (d = 21 cm, h = 18 cm). The twill is 3/3. The basket weaver used in one direction brown coloured strands and in the other direction strands of natural colour to accentuate the intended multicentric designs. A main centre of dimensions 5×5, several local centres in form of concentric squares of dimensions 5×5 and 3×3 (see Figure 21) and several local centres in form of an X of dimensions 5×1 and 1×5 (see Figure 22) may be observed both on the lid and the base. It may be noted that a horizontal 3×3 centre seems, seen from the inside of the basket, a vertical centre, and vice-versa. Figure 23 presents the structure of the lid of a nivuku. This time the twill used is 2/2. The structure displays three vertical and three horizontal lines of weaving discontinuity. The six discontinuity lines are double lines. They generate five centres (one main centre and four local centres) in form of concentric squares of dimensions 4x4 (three times) and of 2×2 (twice) (see Figure 24) and four local X-centres of dimensions of 2×4 and 4×2 (see Figure 25). It may be noted that the X-centres of
dimensions 4×2 and 2×4 are similar: it is enough to rotate
the nivuku around the main centre about a right angle to change
the X-centres of dimensions 4×2 into X-centres of dimensions 2×4,
and vice-versa.
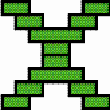
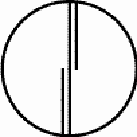
Three exceptional Mavuku Three mavuku present very interesting particularities. Photograph 3 displays the only nivuku observed that does not possess a circular rim. The rims of the lid and of the base are more or less elliptic (h = 17 cm, larger diameter = 28 cm, smaller diameter = 22,5 cm). This form was certainly difficult to achieve because the natural form of the curved, closed rim is circular, being the circular form a consequence of the equal distribution of the tension along the rim. When tying the mat to the wooden rim, the basket weaver had to exercise quite a lot of pressure on the rim to guarantee that it assumed the intended oval-elliptic form. Figure 26 presents the multicentric structure of the elliptic lid. The twill is 3/3. Figure 27 presents the real image of the lid. This image enjoys an axial symmetry. In the vertical direction the basket weaver used brown coloured strands, with the exception of the two single discontinuity lines. In the horizontal direction he used strands of natural colour with the exception of the two brown coloured strands that constitute the central, double discontinuity line. Centres in the form of concentric squares of dimensions 1×1, 3×3, 5×5, 6×6, 8×8 (variant a) and 2×1 appear on the lid of the elliptic nivuku (see Figure 28). Figure 29 presents the structure of concentric toothed squares at the base of the elliptic nivuku. It seems that the centre is placed at one of the focuses of the ellipse. The basket weaver used several bands of coloured strands in the two weaving directions. A consequence of the elliptic shape is that the lid can only be placed in two positions to close the nivuku. In the case of a circular nivuku, the lid can, in principle, be placed in any way. Nevertheless, as the circular rim is never exactly circular, the basket weaver marks often two signs on the upper and lower rim that should be aligned to facilitate the closing of the nivuku and to align the decorations of the upper and lower rim. The 2/2 twill was used to produce the other two exceptional mavuku. In the first case, the basket weaver used for the base of a small nivuku (h = 14,5 cm, d = 21 cm) one central discontinuity line, flanked by two discontinuity half-lines (see the diagram in Figure 30). He invented a weaving structure that has a rotational symmetry of 180 degrees. Around its centre (Figure 31a) one can rotate the basket about a straight angle without changing its appearance (see Figure 31b). In the second case, the basket weaver
used the diagonal weaving structure without introducing any discontinuity
line, but he introduced in a systematic way coloured strands such that
a plane pattern of L’s appears (see Figure 32). Both
in the horizontal (Figure 33b) and in the vertical
direction (Figure 33c), a brown coloured strand is
introduced after each group of three naturally coloured strands.
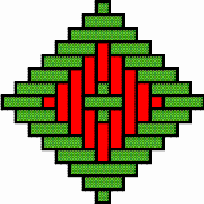
Lessons from the master-weaver Mulaliha In our collection we have one very particular nivuku (d = 25,5 cm, h = 18 cm). The finish and the decoration of the rim are not of high quality. The texture of its base presents a structure of concentric toothed squares with master Mulaliha’s signature. The lid is not bended in a uniform way. I am under the impression that we are dealing with a basket produced by the student of the master. The curator of the National Museum of Ethnography in the City of Nampula informed me that the old Mulaliha had been working all alone. Collaborators of the Museum tried to convince him to teach his knowledge to somebody of his community in order to avoid that, with his death, the knowledge, the art and the technique of making mavuku would disappear from his region. Subsequently, in 1999, Mulaliha found a man of about fifty years interested to learn to produce mavuku. I suppose that the student made this particular nivuku. The lid has an extraordinary weaving structure,
little visible because the basket weaver used in both directions only strands
of natural colour. To increase the visibility I present in Figure
34 the structure of the lid in such a way that the vertical strands
appear coloured. The twill is 3/3. In the main centre the master’s signature
appears, surrounded by local centres of several dimensions, 1×1,
5×5 (horizontal), 5×5 (vertical), 2×1 and 5×6 corresponding
to the general twill of 3/3, and one centre of dimensions 1×2 (see
Figure 35), exceptionally corresponding to the twill 2/2. On the lid horizontal
X-centres of dimensions of 1×5, 5×1, and 5×2, and vertical
X-centres of dimensions 1×5, 1×6, 2×5, 5×1, and
5×2 (vertical) appear. It seems that the master basket weaver Mulaliha
was teaching his student the possibilities of creating different centres
in form of an X and in form of concentric squares. In this sense the basket
lid constitutes the student’s notebook.
Conclusion Mavuku weavers explore, globally and locally, rotational and bilateral symmetries. They may produce special effects, including plane patterns, by the use of brown coloured strands next to naturally coloured strands. I hope that the publication of the paper
may contribute to the valuing of the knowledge, know how and legacy of
the mavuku weavers as an interesting facet of Makhuwa culture.
Acknowledgements I thank Pedro Kulyumba and Ulla Rosenquist, director and curator, respectively, of the National Museum of Ethnography in the City of Nampula. They gave me the unique opportunity to visit, in May of 2000 and April of 2001, the warehouse of the Museum and to observe dozens of mavuku acquired by the Museum for resale in its store-gallery. There I had the possibility to select and to acquire some mavuku in function of their designs. Other mavuku were acquired in stores and marketplaces in the cities of Nampula and Maputo. At present these mavuku are exhibited at the Ethnomathematics Research Centre in the capital Maputo. I thank my daughter Lesira and my colleague Abdulcarimo Ismael for their interest and for accompanying me in the visits to Nampula Province. I thank György Darvas for his invitation
to contribute a paper to the special issue on "Ethnomathematics and Symmetry"
of "Symmetry: Culture and Science."
The 2/2 and 3/3 twills
Single and Double Discontinuity lines in the case of the
3/3 twill
(a)
(b)
Two double discontinuity lines
Four quadrants and design of successive toothed squares
a
b
c
d
e Central structures of designs of successive toothed squares
in the 3/3 case
Central structure of the only observed design of successive
toothed squares in the 2/2 case
Texture of concentric toothed squares with a 6×5
centre
The two variants of the 8×8 centre
Texture with the first variant of the 8×8 centre
a
b
Centre in form of a X of dimensions 5x1
Multicentric texture of the lid of a nivuku
A centre in form of an X of dimensions 1×5
a
b
Dimensions 2×4 a
Dimensions 4×2 b Centres in form of an X
Multicentric texture of the lid of the elliptic nivuku
The structure of the base of the elliptic nivuku
Centre with rotational symmetry
Texture of the exceptional lid
References Cherinda, M. (2002)
The Use of a Cultural Activity in the Teaching and Learning of Mathematics:
Exploring Twill Weaving with a Weaving Board in Mozambican Classrooms
(unpublished Ph.D. thesis), Johannesburg: University of the Witwatersrand
Gerdes, P. P. (1990)
On ethnomathematical research and symmetry, Symmetry: Culture and Science,
Budapest, Vol.1, No. 2, 154-170
___ (1990a) Ethnogeometrie.
Kulturanthropologische Beiträge zur Genese und Didaktik der Geometrie,
Bad Salzdetfurth: Verlag Franzbecker, (reprinted in 2002)
___ (1999) Geometry
from Africa: Mathematical and Educational Explorations, Washington
DC: The Mathematical Association of America
___ (2000) Le
cercle et le carré: Créativité géométrique,
artistique, et symbolique de vannières et vanniers d’Afrique, d’Amérique,
d’Asie et d’Océanie, Paris: L’Harmattan
___ (2000a) Gerade
und Ungerade – Zu einigen mathematischen Aspekten der Mattenflechterei
der Yombe-Frauen am unteren Kongo, In: Blankenagel, J. and Spiegel, W.,
eds., Mathematikdidaktik aus Begeisterung für die Mathematik. Festschrift
für Harald Scheid, Stuttgart: Ernst Klatt Verlag, 83-93
___ (2002) Twill-Plaited
Octagonal designs, Visual Mathematics, Vol. 4, No. 3, September
2002 (http://members.tripod.com/vismath8/gerdokt/index.html)
___ (2003) Awakening of Geometrical Thought in Early Culture, Minneapolis MN: MEP Press, 200 pp. ___ (2003a) Sipatsi: Cestaria e Geometria na Cultura Tonga de Inhambane, Maputo: Moçambique Editora, 176 pp. ___ (2004) Symmetries on Mats Woven by Yombe Women from the Lower Congo Area: On the Interplay between Cultural Values and Mathematical-Technical Possibilities, In: Washburn, Dorothy K. & Crowe, Donald W., eds. Symmetry Comes of Age, The Role of Pattern in Culture, University of Washington Press, Seattle, 2004, 81-99 Gerdes, P.P. & Bulafo, G. (1994) Sipatsi: Technology, Art and Geometry in Inhambane, Maputo: Universidade Pedagógica Guss, D. (1989) To Weave and to Sing, University of California Press, Berkeley LaPlantz, S. (1993) Twill Basketry, A Handbook of Designs, Techniques, and Styles, Asheville NC: Lark Books Sentance, B. (2001) Art of the Basket, Traditional Basketry from around the World, London: Thames & Hudson
|