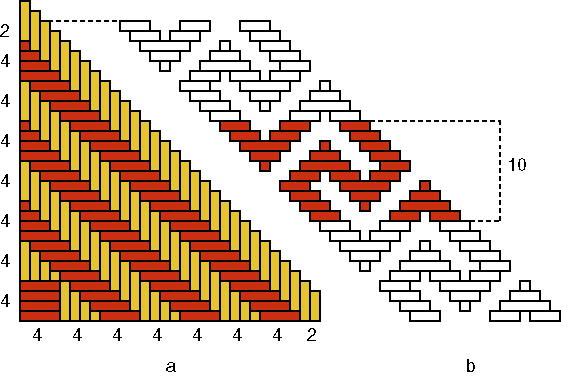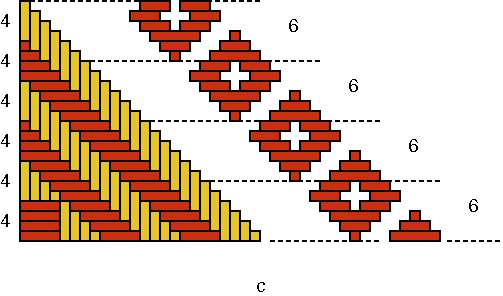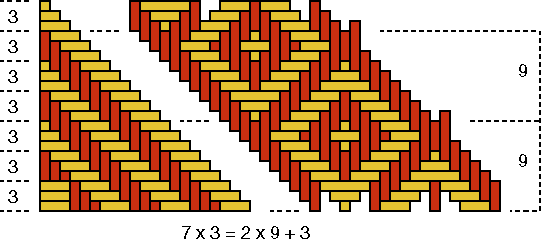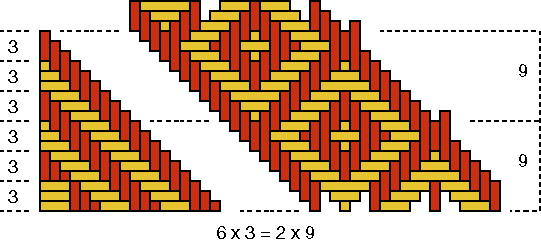Paulus Gerdes

Mozambican Ethnomathematics Research Centre, C.P. 915, 
Maputo, Mozambique 
pgerdes@virconn.com
 

Abstract: The paper analyses four cylindrical baskets from the Brazilian Amazon that have a square base. The relationships between the number of strands on each quadrant of the basket bottom and the period of the decorative designs on the basket wall are studied. Reasons for possible mistakes by the basket weaver are explored.
 
 

Cylindrical baskets with square base

In regions of the world situated far from each other, cylindrical baskets with a square base are produced, whereby the strands are woven in such a way that they make angles of 45^o both with the sides of the base and with the circular border. They are found, for example, among the Carajá, Timbira, and Guajajara of eastern Brazil, in Guyana, in Indonesia, in Laos and in the Philippines; and among the Makonde of northern Mozambique.

Photograph 1 shows four baskets of this type I acquired in Brazil in 1988. In (Gerdes 1991; 2003, pp. 69-77) I analysed some considerations of a geometrical nature that played a role in the invention of this type of basket. Now I shall analyse, on the basis of the baskets illustrated in the photograph, some mathematical thoughts that underlie their ornamentation.
 
 

Wall ornamentation

By interlacing strands of different colours – black-brown in one direction, and yellow-white, in the other direction, perpendicular to the first –  beautiful patterns may be produced, when weaving mats (see the example in Figure 1).

At first sight it may appear that interlacing two such groups of strands of different colours produced the baskets in Photograph 1. Had this been the case, however, then black-and-white ornaments never could have decorated their cylindrical walls! The explanation can be found in the special weaving technique of these cylindrical baskets with square base. Each strand leaves the base at two places. As the scheme in Figure 2 shows, the strand climbs up, on one side, in a left turning helix and, on the other side, in a right turning helix. In this way each strand intersects itself – and all other strands that on the base were parallel to it – on the cylindrical wall. When one observes more closely the bases of the Brazilian baskets (see Photograph 2 and the example in Figure 3), one sees that all strands are of a particular sort: of each strand exactly one half is black (see Figure 4). Each base – with a design composed of various concentric "toothed squares" – displays a rotational symmetry of 90^o; its four quadrants are also colour-congruent (cf. the base of basket D in Figure 3 with the plaited square in Figure 1). By consequence, all the left turning helices are black and all the right turning helices are white (as in the cases of the baskets A and B in Photograph 1). Or conversely, all the left turning helices are white and all the right turning helices are black (baskets C and D). In this manner the artisans solved creatively the problem: on the walls blackened pieces of strand always cross white parts of strand. This solution made it possible for them to copy their plane ornamental patterns – displayed on woven mats or basket bowls – on the walls of their cylindrical baskets with square base.

With the so obtained possibility to decorate the walls of this type of basket, there emerged simultaneously a completely new problem. When decorating plane mats, one copy of the pattern motif could always be plaited next to another copy. In principle the mat was unlimited. The cylindrical wall, however, is limited: not always is it possible to weave a copy of the motif (horizontally) next to another copy. This is possible only then when there is still sufficient place to do so, that is, when the number of "free"- standing neighbour pieces of strand is at least as high as the number of strands necessary to produce a copy of the decorative motif. To guarantee the continuity of the ornamentation, that is, to guarantee that the ornamentation of the basket displays a rotational symmetry – this presupposes this symmetry as an aesthetic value or, at least, if this value already existed, it develops further in this process of invention – the artisan is obliged to choose the (total) number (N ) of strands in such a way that there is on each horizontal level of the cylindrical wall place for exactly a certain whole number (P ) of copies of the decorative motif. In other words, it holds that

Q denotes the "width" or the "period" of the decorative motif, that is the number of strands (in one direction) that generate the motif.

As the base is built up out of four congruent quadrants (see Figure 3), the number (N ) of strands is always the fourfold of a smaller natural number (n):

In other words, each quadrant generates a quarter of the wall. When one likes to repeat p times a decorative motif on each quarter of the wall, it must be true that:

This implies that:

or P is divisible by 4. In the concrete case of the four baskets, it may be seen that P is actually always divisible by 4:

It may be concluded that the inventors of this type of decorated baskets were probably aware of this (simplified) relationship:

Q depends on the selected decorative motif. The number of repetitions of the motif can, in principle, be freely chosen. The values of p and Q determine the number (n) of the strands that the basket weaver needs (in one direction) for one quadrant of the base.
 
 

Basket A

Figure 5b shows that the width or period of the motif of basket A is equal to 10:

As p(A) = 3, the following has to be valid:

One quadrant of its base is illustrated in Figure 5a. The number n(A) of strands in one direction, for example, the number of white pieces of strand can be counted in groups of four; two pieces of strand remain at the end:

This leads me to assume that the inventor(s) of this type Aknew that

Remains open the question, how and in what form (s)he/they might have acquired this knowledge. Maybe by means of side by side placement of mats which were decorated by both black-and-white patterns?

If one observes basket A more precisely, one notes that not all copies of the motif have width 10:
 
 

Some have width 9, others 11 and one even 13; only the average width is 10. We are dealing here with a "slovenly" woven basket, most probably a quickly produced imitation of an older basket. Although the base had been well copied, the artisan was not so worried about the precision (that is, all motif elements with the same width). Nevertheless, if its inventor had not aimed at precision, he/she could have been satisfied with 7×4 instead of 7×4+2 strands for each quadrant. This reinforces my assumption that the choice of 7×4+2 strands per quadrant was not at all accidental, but the result of calculation (7×4+2 = 3×10). This calculation might have been, as said already before, of a geometric nature. On the contrary, it is well possible that the imitator was not aware, in this context, of the relationship:

(S)he had only observed or learnt in one way or another that for this model 7×4+2 strands per quadrant were needed.

My analysis of the first basket (A) raises immediately the question, what the relationship between the possible original and the supposed imitation in the cases of the baskets B, C and D will be like.
 
 

Basket B
 
 

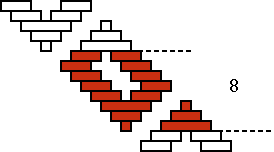
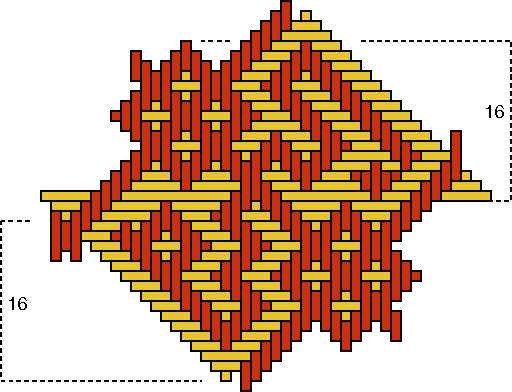
Photograph 3 displays the reverse sides of baskets B, C and D. Besides the 16 plaited squares [P(B) = 16], there appears on the wall of basket B yet a rectangle with a width of 8 strands (see Figure 6). This rectangle breaks (or eliminates) the continuity or the symmetry of the whole ornamentation. Was it aimed for or was it maybe an error or a mistake?

Let us assume that is was not aimed at. How can its appearance then be explained?

Figure 7b shows that the period of the plaited square is equal to 6:

As P(B) = 16 and therefore p(B) = 4, the following must held for the number n(B) of strands per quadrant:

Figure 7a presents one quadrant of the base of basket B. The strands can be counted in groups of 5 and 4:

With our mathematical knowledge we may note that this quantity 2×5+4×4 is equal to 26 and therefore 2 more than the necessary quantity 4×6 or 24. As there are in each quadrant two strands too much, there are in total 8 more strands than desired. Only at the moment that the basket weaver completes his/her series of squares and tries to interlace the last square, he/she remarks that this is not possible. He/she has too many strands and obtains a rectangle that is not square (with a weaving width of 8 strands). Now, it is already too late to correct his/her error. The only way to do so would be to start again.

Indeed, it was possible to explain the appearance of the non-square rectangle in the decoration of basket B, but it remains to be shown where the error/mistake has been made. We saw that the strands of one quadrant of the base of this basket can be enumerated in groups of 5 and 4:

Why groups of different width? What happens if all groups have the same width?

When the groups in the centre of the base possess a width of 4 instead of 5 strands, as in Figure 8a, then there are all together 6 groups of 4 strands. In other words, the following is valid:

With our mathematical knowledge we see immediately that this number 6×4 is indeed equal to the necessary number n(B) = p(B) × Q(B) = 4×6. The mistake is clear: both groups of 5 strands should have been groups of 4. Most probably are we dealing with a reproduction error, during the imitation of an older basket. The inventor of this decorated basket was aware of the fact that to generate four times a plaited square of width 6, six groups of four strands are sufficient (Figure 7c). The inventor knew in one form or another that

How could this knowledge have been acquired? In what measure became it generalized (commutativity of the multiplication)?

In the analysis of basket B, I assumed that the appearance of the non-square rectangle in both layers of squares on the wall was not aimed at. Would it have been intentional, one might only say that the aim was achieved.

Besides eight plaited square "windows" [P(C) = 8], one finds in basket C on each of the three horizontal series a rectangular "window" (see Photograph 3c), with a weaving width of 12 strands (see Figure 8). As in the previous case, the question arises if the artisan aimed for this extra "two-eyed" rectangle – that eliminates the continuity of the whole ornamental band –or not. I assume that we are dealing once again with an error, that may be explained as follows.

Figure 9a (right side) shows that the period of the woven "window" is equal to 9:

As P(C)=8 and therefore p(C)=2, the number n(C) of strands per quadrant must be:

As a quadrant of the base of basket C has in reality 7×3 strands in each direction (see Figure 9a, left side) and as is valid

This also can be concluded geometrically, as Figure 9a shows. There are all together 4 times 3 or 12 strands too much. Both (left- and right turning) groups of these 12 remaining strands have been interlaced to form the two-eyed "window." From the left and from the right the artisan tried to weave a normal square, one-eyed "window", what happened to be impossible; the two one-eyed "windows" "melted" necessarily together to a beautiful two-eyed "window". That there resulted a beautiful ornament was good luck. The weaver of basket D was in this respect less lucky, as we shall see soon. The error of the maker of basket C is clear. In each quadrant there is one group of three strands too much: 7 times 3 strands instead of 6 times 3 strands. For one reason or another (s)he miscounted. Also here are we dealing most probably with a mistake in the reproduction. The inventor of the original ornamentation that underlies the decoration of basket C was conscious of the fact that, to generate two times a plaited "window" with a weaving width of 9, six groups of three strands are necessary. In other words, the inventor knew in one way or another, that

Figure 9b shows how the original quadrant would have looked like and how it produces exactly two times the patterns’ motif.
 
 

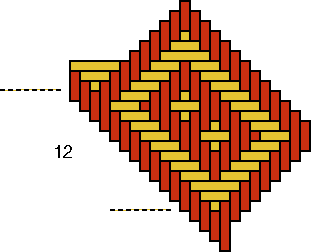
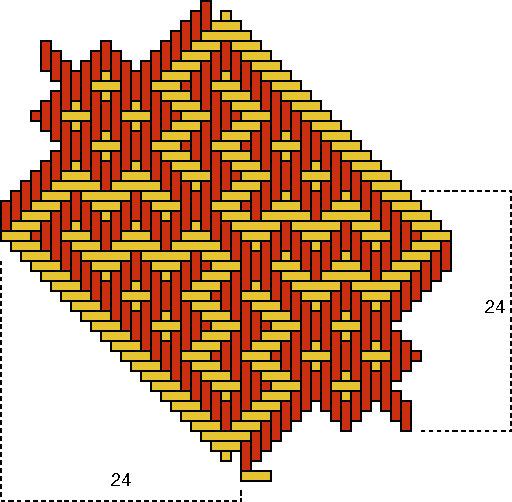
Basket D

Besides four times the beautiful "monkey" design, one observes on basket D still a fifth figure. This last figure possesses a weaving width of 16 strands, as shows Figure 11. On the contrary, the "monkey" with its two perpendicular axes of symmetry, has a weaving width of 24 strands [see Figure 10c; Q(D)=24]. As P(D)=4 and therefore p(D)=1, the following has to be true for the number n(D) of strands for one quadrant:

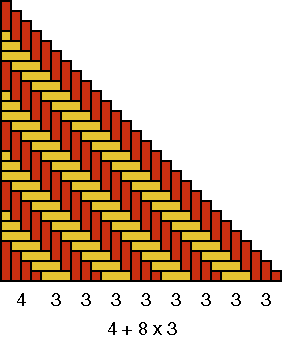
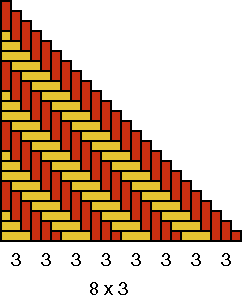
A quadrant of the base of basket D is displayed in Figure 11a. The strands may be counted, in each direction, in groups of 4 and 3:

As

the eight groups of three strands were sufficient to produce the decorative motif. Now, however, there are in the centre of the base still four times four or 16 strands too much. This caused the extra figure on the wall of the basket. The weaver tried to interlace one more "monkey" (cf. the bottom sides of Figures 10c and 11), but he/she did not succeed. Most probably we are dealing also in this case with a reproduction error. The inventor of the basket with the "monkey" motif knew, that he/she needed 8 groups of 3 strands to produce one exemplar of the decorative motif:

Figure 10b shows how the original quadrant should look like. Possibly, the artisan changed the necessary base structure of basket D with that of another type of basket. As we know that

the other basket type had a design element with a possible width of 4, 7 or 14 strands.
 
 

Concluding remarks

I obtained baskets A, B and C in Rio Claro (São Paulo State). As it was explained to me in the shops, the baskets came from the Brazilian Amazon. The last basket was given to me in São Paulo City. It comes from the Kamayurá village of the Wai-Wai Indians in the Northeast of Brazil. As the selling price was relatively low – between 2 and 3 US dollars – and their makers probably received much less for them, my assumption is reinforced that we are dealing with quickly fabricated baskets, whereby the artisans were not very worried about precision – the buyers would hardly remark, estimate and value a higher precision. This apparent lack of care can explain the weaving errors I analysed. It implies not, however, that the makers were not capable of that precision. For them to survive it seems not worth while to do the calculations to guarantee the continuity of ornamentation on the basket wall.

The inventors of the continuous basket wall motifs, however, had a precise knowledge of the geometric-arithmetic connections between wall- and base designs. It would be interesting to reconstruct this knowledge and its transmission from generation to generation. It seems interesting and important to deepen this analysis and to pursue the research. To do so it is indispensable to do fieldwork among various communities and to analyse baskets that may be encountered in museums. On the basis of this study, it would be interesting to reflect about the possible influence of the type of the uncovered knowledge of basket weaver-artists on the development of the rest of mathematical thinking among the Amerindians and, in particular, on the ancient Indian civilisations of Peru and Mexico. 

Besides the historical importance, the continuation of this study can be useful also in the educational field: valuing the past and present of the indigenous peoples, incorporating elements of their scientific knowledge, including mathematical knowledge, into education in Brazil and elsewhere.