| Some designs on twill plaited
baskets and mats from Angola Paulus Gerdes Mozambican
Ethnomathematics
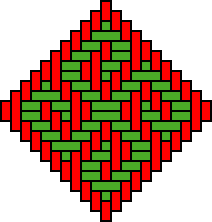
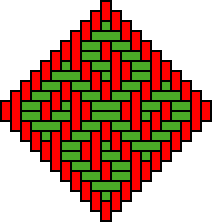
The following chapter presents examples of designs, patterns and the combination of designs on twill plaited baskets and mats from Angola, mostly from the Lunda region in the Northeast. The presentation is based on an analysis of objects present in the Dundo Museum (Angola, cf. Bastin, 1961), the Anthropological Museum (AMC) of the University of Coimbra (Portugal), and the National Ethnographic Museum (NEM) in Lisbon (Portugal, cf. Gerdes, 2002). Among the twill woven circular trays in the aforementioned museums, are several trays with carefully conceived centres that display two axes of symmetry. Figures 1, 2 (cf. Gerdes, 2000, p. 147) and 3 present three examples (NEM AI 478, AMC 80.34.69, NEM AE 598) . Figure 4 presents a detail of a Cokwe mat (NEM AG 378), composed of 25 identical toothed squares. On another Cokwe mat (NEM AG 379), there is a large toothed square composed of 121 of the same small toothed squares (3, 2, 3). On this mat there is also a large toothed square with 16 small toothed squares of the (1, 3, 3) type (Figure 5). Figures 6, 7, 8 and 9 show four Cokwe designs (Bastin, 1961, p. 116). On the first a composition of 9 small toothed squares of the (1, 2, 3) type appear. On the second 36 small toothed squares appear. Each of them has a visual image that displays a horizontal two-colour symmetry axis. On the third and fourth (Figures 8 and 9) appear plane patterns with two- and fourfold symmetry, respectively. Figure 10 displays the design motif with which a Yombe mat from the Cabinda enclave (NEM AO 174) is patterned. It may have been derived, in a similar way as the Kongo designs from the 17th century (see chapter "Delicately decorated seventeenth century Kongo baskets"), from the woven design in Figure 11. Another square mat from Cabinda is very spectacular (NEM AO 949). Around the large central toothed square, a pattern is woven that imitates the 1/1 plating where the small holes between the strands are substituted by identical toothed squares (see Figure 12). In the large central toothed square there appear nine toothed rectangles (almost squares) of dimensions 29x30 of two types A and B (see Figure 13a and b). The first one is the vertical mirror image of the second. Figure 14 displays the distribution of the toothed rectangles on the large central toothed square. Variant A appears on the vertical axis whereas variant B appears only outside the central axis. The mat weaver created the impression that the design motifs A and B have a 90 degrees rotational symmetry. Moreover when one observes the design it gives the visual impression that A and B have also an oblique axis of mirror symmetry (see Figure 15). The toothed rectangles C and D (Figure 16) are almost square and have dimensions 21×22. They appear on a delicately woven mat from Cabinda (NEM AO 950). The toothed rectangles C and D are grouped in five sets of nine each (see the diagram in Figure 17). The groupings are realised in three distinct ways (see the schemes in Figure 18). The groupings have a vertical axis of symmetry. The design motifs themselves have a twofold symmetry, although they give the impression of displaying a fourfold symmetry. Figures 19 to 21 display in detail the larger toothed rectangles with dimensions 73×74.
Fig. 1: Central toothed square of a Lunda
circular tray
Fig. 2: Central toothed square of a circular tray
Fig. 3: Central part of a Lunda circular
tray
Fig. 8: Cokwe plane pattern with twofold
symmetry
Fig. 9: Cokwe design with plane pattern
with fourfold symmetry
Fig. 11: Possible original design
Fig. 14: Distribution of toothed rectangles
Fig. 18: Three ways of grouping
Fig. 19: First larger toothed rectangle
Fig. 20: Second larger toothed rectangle
References Gerdes, Paulus, Le cercle et le carré: Créativité géométrique, artistique, et symbolique de vannières et vanniers d’Afrique, d’Amérique, d’Asie et d’Océanie, L’Harmattan, Paris, 2000 Gerdes, Paulus, Padrões de entrecruzamento em esteiras e cestos de Angola (conservados no Museu Nacional de Etnologia, Lisboa), research report, Ethnomathematics Research Centre, Maputo, 2003 |