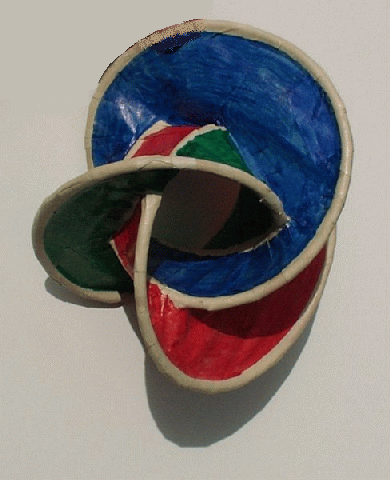|
Knots
and Multiple Mobius
Nat Friedman The 2-3 torus knot admits a minimal surface consisting of two Möbius bands that share edges and alternately cross over each other. In Figure 1 we see a red Möbius band and a blue Möbius band on a 2-3 torus knot. There is a space in the center. 
Figure 1 Another view is shown in
Figure 2 where we see the blue band crossing the red
band at the top and the red band crossing the blue band at the bottom.
Figure 2 The 3-4 torus knot admits
a minimal surface consisting of three Möbius bands that share edges
and alternately cross over each other. In Figure 3 there
is a minimal surface on a 3-4 torus knot consisting of red, blue and green
Möbius bands with a space in the center. We see the blue band crossing
over the red and green bands at the top. In the center the green band crosses
over the blue and red bands. The detail in Figure 4 shows
how the green band moves to the right of the red band after crossing over
the blue and red bands. Similarly, the blue band will move to the right
of the green band after crossing over the red and green bands.
Figure 3
Figure 4 In general, the n-(n+1)
torus knot will admit a minimal surface consisting of n Möbius
bands that share edges and alternately cross over each other.
|