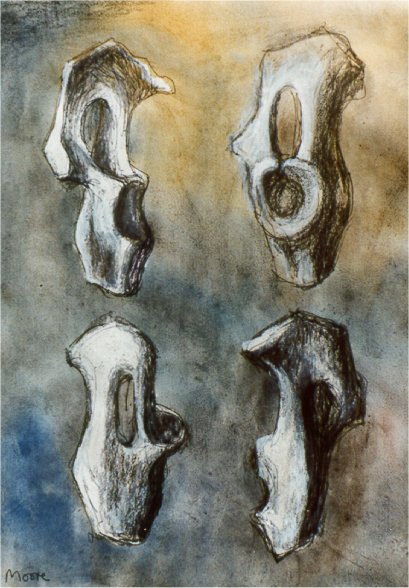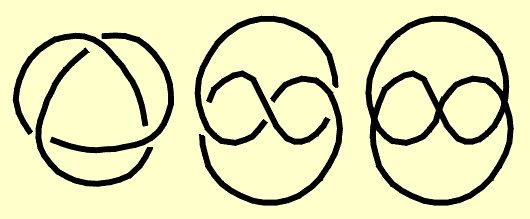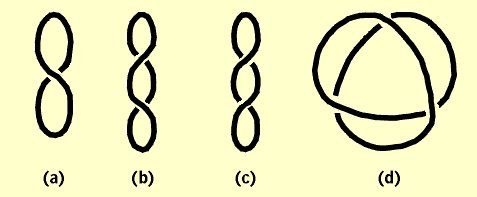|
and Space Curves Nat
Friedman
E-mail: artmath@math.albany.edu
Abstract Our
purpose is to relate hyperseeing and hypersculptures to space curve sculptures
derived from knots. We will include an introduction so that the paper is
self-contained, as well as discuss several examples.
Introduction The operative word that unifies art and mathematics is SEEING. More precisely, art and mathematics are both about SEEING RELATIONSHIPS. One can see certain mathematical forms as art forms, and creativity is about seeing from a new viewpoint. As the Basque sculptor Eduardo Chillida states "to look is one thing, to see is another thing", "to see is very difficult, normally", "to look is to try to see" [1]. An excellent related article is Levine's See-Duction [5]. Let's first look at an example from mathematics and try to see. Consider the four by four checkerboard shown in Figure 1.
Figure 1 Now we see four rows of four so we have 4 + 4 + 4 + 4 = 16. We also see eight white squares and eight black squares so we have 8 + 8 = 16. What else can you see? Well if you look at the diagonals, you see that starting at the upper right there is one white square, two black, three white, four black, three white, two black, and one white. So we have 1 + 2 + 3 + 4 + 3 + 2 + 1 = 16 (1) Now do you see a relationship in (1)? Well 4 is the middle term and 42=16. Can you now guess 1+2+3+4+5+4+3+2+1=? (2) The
symmetric sums in (1) and (2) lead to the following general formula
1 + 2 + 3 +. . . + (n - 1) + n + (n - 1) + . . . + 3 + 2 + 1 = n2. (3) The relationship in (3) can be seen in an n x n checkerboard. Let's now consider an example of the vision of the British sculptor Henry Moore. A view of a cow bone is shown on the right in Figure 2.
Figure 2 I gave Moore a duplicate of this bone during a visit to his studio on April 2, 1980. I recall that he immediately started running his finger back and forth in the groove of the bone. He did a drawing of this view which appears in his 1980 sketchbook, and is shown on the left in Figure 2. Now the interesting point is that he also saw ideas in the less atractive side of the bone on the right in Figure 3. This surface resulted after the whole leg bone was cleaned in boiling water and this part detached from one end of the leg bone.
Figure 3 More saw the bone as a hooded figure and used the hollow in the lower right as a space to hold a child. He kept the groove in the lower right part and removed the left side. The resulting bronze sculpture Mother and Child Hood is shown on the left in Figure 3. There is also a seven foot version in white le in Saint Paul's Cathedral in London. This is just one example of how Moore could transform a natural object into a figurative sculpture. In mathematics one often considers an isomorphism (same form). One can say that Moore saw isomorphisms between rolling hills and reclining figures, between bone forms and figures, as well as between shells and tree root forms and figures. In mathematics a topological example of a surface with one side and one edge is the familiar Möbius band. A model is obtained by twisting a strip of paper and gluing the ends together. The Swiss sculptor Max Bill based the granite sculpture Endless Ribbon on the shape of a Möbius band and is shown in Figure 4. This is an excellent example of seeing a mathematical form as an art form.
Figure
4. Max Bill: Endless Ribbon, Pompidou Center, Paris
Hyperseeing The preceeding examples show how learning to see is of fundamental importance in both art and mathematics. We note that the recent 1998 Mathematics Awareness Week was devoted to diverse applications of imaging in the sciences. Whole new worlds open up when one is able to see better, whether it is the Hubble telescope, refined microscopes, or magnetic resonance imaging. New ways of seeing can have diverse applications. We will now discuss a more complete way of seeing a three-dimensional object that is called hyperseeing. First we note that in order to see a two-dimensional painting on a wall, we step back in the third dimension. We then see the shape of the painting (generally rectangular) as well as every point in the painting. Thus we see the painting completely from one viewpoint. Now theoretically, to see a three-dimensional object completely from one viewpoint, we would need to step back in a fourth dimension. From one viewpoint, we could then (theoretically) see every point on the object, as well as see every point within the object. This type of all-around seeing, as well as a type of x-ray seeing, was known to the cubists such as Picasso and Duchamp, as discussed in [3]. In particular, cubists were led to showing multiple views of an object in the same painting. In
mathematics four-dimensional space is referred to as hyperspace
and I refer to (theoretical) seeing in hyperspace as hyperseeing.
Thus in hyperspace one could hypersee a three-dimensional object completely
from one viewpoint.
Hypersculptures Although we do not live in hyperspace, it is still desirable to attain a type of hyperseeing. This is facilitated by viewing a hypersculpture defined as follows. First, a sculpture is defined as an object in a given orientation relative to a fixed horizontal plane (the base). Two sculptures are said to be related if they consist of the same object in different orientations. A hypersculpture is a set of related sculptures. There are abstract three-dimensional objects that have several interesting orientations. To more completely appreciate the diverse sculptural content of the object, it is natural to present it as a hypersculpture. Furthermore, the experience of viewing a hypersculpture allows one to see multiple views from one viewpoint which therefore helps to develop a type of hyperseeing in our three- dimensional world. Viewing a hypersculpture is really a new visual experience. It is a more complete way of seeing a three-dimensional object. The concept of a hypersculpture was motivated by the work Attitudes by Arthur Silverman, shown in Figure 5.
Figure
5. Attitudes, Arthur Silverman, Hypersculpture,
Attitudes
is a hypersculpture consisting of six copies of the same object, each on
a separate base. The object consists of a rectangle, parallelogram, and
two triangles. People viewing the six separate sculptures do not even realize
that it is the same object. Thus Attitudes is an excellent example of how
a hypersculpture presents the three-dimensional content of an object more
completely.
Substructures A hypersculpture consisting of five copies of an object is shown in Figure 6.
Figure 6 The object in Figure 6 is a black rectangle and a white triangle, each made of foamcore, and joined edge to edge using a toothpick piercing the styrofoam edges. The view is from above and the photograph was taken in strong sunlight to emphasize the shadows. Let
us denote the hypersculpture by H. The basic object consists of
two elements, a triangle and a rectangle. Let t denote the triangle
and let r
denote the rectangle. If we concentrate just on t,
then we see
t in five orientations. Thus in each sculpture in H
we can regard t in its orientation as a one-element subsculpture. The five
subsculptures consisting of just t will be denoted by Ht.
Note that Ht
is a more complete presentation of the three-dimensional
content of t. Similarly Hr is a more
complete presentation of the three-dimensional content of the rectangle
r.
Thus in this case we could say that H contains two subhypersculptures
Ht and
Hr.
Higher Order Hypersculptures In Figure 6 we have five copies of a basic object in H, and we refer to H as a first order hypersculpture. We will now consider a hypersculpture consisting of two copies of the preceding basic object, except here the copies will more closely relate to each other, as in Figure 7.
Figure 7 Here the point of one triangle is resting on the other rectangle. This hypersculpture is also a first-order hypersculpture. Although this is a hypersculpture with the object in two distinct orientations, one can also see this hvpersculpture as an object . As an object, we are also aware of the spaces between the four elements consisting of the two triangles and two rectangles. A hypersculpture based on the object in Figure 7 is shown in Figure 8 below. Here we have simply rotated one object 90o relative to the other object. The main point is that the spatial relations between the elements are also seen differently in each sculpture. We refer to the hypersculpture in Figure 8 as a second-order hypersculpture since the basic object is a first order hypersculpture.
Figure 8 When we consider the substructures in Figure 8, there is quite a lot to see. We can refer to the four basic elements in the object in Figure 7 as two triangles t1 and t2 and two rectangles r1 and r2. In general, there are 24 = 16 subsets of four elements including the trivial empty set. Thus there are 16 - 1 = 15 non-trivial subojects to consider in Figure 7. Hence there are 15 subhypersculptures to consider in Figure 8. For example, if we consider just the two triangles, then we see the space between them quite differently in each subsculpture in Figure 8. We could also consider the two rectangles or the two triangles and one rectangle, etc. Thus there is a lot to see in examining the substructures. Let us denote the second-order hypersculpture in Figure 8 by H2. We could consider H2 as a basic object in a third-order hypersculpture H3. Note that H2 has eight elements so H2 has 28 - 1 = 255 non-trivial subjects. Thus H3 would have 255 subhypersculptures, which is really a lot to look at!! In general, we can say Hn+1 is an (n+1)st order hypersculpture if the basic object in Hn+1 is an nth order hypersculpture Hn , n ³ 1. The real quest is to create objects that yield hypersculptures with visually interesting form-space relationships. In
general, experience with hypersculptures also motivates an increased appreciation
of sculpture since one learns to look harder and more closely from all
angles. The book
As The Eye Moves
[2] consists of numerous photographs by David Finn of
the Henry Moore three piece reclining figure Bridge Prop. Finn has made
a wonderful study of Bridge Prop with many close-up detail views as well
as all-around views. This is an excellent book from which to learn how
to more completely experience a sculpture.
Henry Moore and Hyperseeing As
mentioned above, hypersculptures are significant because they allow for
a more complete appreciation of the three-dimensional content of an object,
as well as enable one to approximate hyperseeing in our three- dimensional
world. One can also consider "hyperseeing" a single sculpture in our three-dimensional
world as described by Henry Moore [4].
Moore
also carved spaces through the form:
From the above quotes we gain a feeling for how Moore saw a sculpture as a composition of shape in both form and space. He saw from all around the sculpture as well as into and through the sculpture. This was Moore's hyperseeing and serves as a definition of hyperseeing in our three-dimensional world. Thus to hypersee a sculpture means to visualize it completely from all- around. Here it is useful to see a top-view of the sculpture, which is not always possible. In Figure 9 we have two views of the Henry Moore sculpture Reclining Figure Angles. Note that the top view helps to really understand the front view.
Figure 9. Henry Moore: Reclining Figure Angles (Private Collection) We note that the top view of a sculpture is rarely shown, which is like leaving out the plan view in architecture. The top view is very helpful in hyperseeing a sculpture.
Figure
10. Henry Moore: Bone Forms (private collection)
Figure 11. Henry Moore: Reclining Figure Circle (private collection) A
drawing by Henry Moore is shown in Figure 10, entitled Bone Forms. This
is really a "hyperdrawing" of a lamb pelvic bone, showing four views. The
interesting point is that later Moore saw this bone horizontally as part
of a reclining figure, as in Figure 11. This shows Moore's ability to hypersee
an object.
Knots and Space Curve Sculptures We will now consider practicing hyperseeing a three-dimensional object. That is, "to visualize a complex form from all around itself, to know while looking at one side what the other side is like". It would be desirable to have an object that is totally three-dimensional with no preferred top, bottom, front, or back. Furthermore, the object should look quite different when viewed from different directions. It would also be preferable to have a form that is open, rather than solid, so that one can see through the form. Fortunately, the mathematical field of knot theory in topology provides an ideal source of such forms. A knot is briefly defined as a curve in space with the ends joined. A knot is usually described by a two-dimensional picture called a knot diagram that shows how parts of the knot cross. A knot projection is a knot diagram without the crossings indicated. A knot projection is like a shadow of the knot. Two diagrams of the so-called trefoil knot are shown in Figure 12 (a) and (b). The projection corresponding to (b) is shown in (c).
Figure 12 If the knots in Figure 12 were made of string, then one could manipulate the form in (a) so that it looks like (b), without cutting the string. In general, two knot diagrams are equivalent if the knot form in one diagram can be manipulated, without cutting, to look like the other form. Briefly, two knot diagrams are equivalent means they correspond to the same knot. A knot diagram is just one view of the knot. In order to really appreciate a knot, one should have a three-dimensional model of the knot. That is, one should have a knot sculpture. One can then see infinitely many diagrams of the knot depending on one's viewpoint. It is easy to make visually interesting sculptures based on knots. Two sculptures made of folded tinfoil are shown in Figure 13. Note that their forms correspond to the diagrams in Figure 12 (a) and (b).
Figure
13
Figure 14 We will refer to a sculpture derived from a knot as a space curve sculpture, or simply a space curve. If one looks at the space curve on the left in Figure 13 from above, one will see a view that is similar to the view of the space curve on the right. The point is that from one knot we obtain infinitely many sculptures depending on the size, material, and shape of the knot. Thus the knot really "comes alive" as a sculpture where one can see infinitely many diverse diagrams, some of which are not obviously equivalent. For example, consider Figure 14, where the space curve is made from 1/4 inch copper tubing. The space curve in Figure 14 is based on the trefoil knot. Note that the view has four crossings. The minimum number of crossings in a trefoil knot is three. In general, knots are classified according to the minimum number of crossings in a diagram of the knot. A loop is simply a knot with zero crossings, sometimes called an unknot. Any diagram with one or two crossings is equivalent to a loop, as seen in Figure 15 (a)-(c). A diagram with three crossings may also be equivalent to a loop, as in (d).
Figure
15
Figure 16 The sculptor José de Riviera [6] made a career out of sculptures based simply on loops. He created beautiful curves in space in highly polished bronze and steel with round or triangular cross sections of varying width. The British sculptors Wendy Taylor and John Robinson have made sculptures based on knot forms. The so-called figure eight knot is a knot with four crossings. A space curve based on the figure eight knot is shown in Figure 16. The view of the space curve in Figure 16 has four crossings. The view of the reflection in the black granite base has six crossings. Here the reflection helps to hypersee the space curve.
Figure
17
Figure 18 A particularly beautiful knot is the ninetheenth knot with eight crossings, denoted in standard knot tables by 819. A tinfoil space curve corresponding to 819 is shown in Figure 17. Note that the crossings alternate in pairs over, over, under, under in the space curve in Figure 17. Knot 819 is the first knot in standard knot tables that does not alternate under, over, under, over, etc. A diagram of knot 818 is shown in Figure 18(a). Note the under, over alteration. The standard diagram of knot 819 in knot tables is shown in Figure 18(b). Note
that the projection of the diagram of knot 818 in Figure 18(a)
is the same as the projection of the diagram corresponding to Figure 17.
This
symmetric
diagram of 819 is not
the standard diagram of 819 shown in knot tables, as in Figure
18(b). In fact, it is not immediately obvious that the diagrams in Figure
17 and Figure 18(b) are equivalent (try manipulating Figure 18(b) into
Figure 17). Beautiful minimal surface sculptures can be obtained by constructing
a knot out of wire and dipping into a solution of soapy water. A very flower-like
minimal surface corresponding to 819 is shown in Figure 19.
Here the center of the surface was punctured to allow the shape in Figure
19 to form. If one looks closely, one can see curves where the surface
intersects itself.
Hyperseeing With Symmetry Symmetry is very helpful for hyperseeing. For example, if an object has a top view with 180' symmetry, then any front and back views are identical. This helps to get an all- around feeling for the sculpture. In Figure 20 is the top view of the Robert Longhurst sculpture Arabesque XXIX. Two front views are shown in Figures 21(a) and (b). Since the top view has 180o symmetry, the view from the opposite side will be the same. The view in (b) is a quarter turn to the left of the view in (a). Knowing that the back view in (a) is the same as the front view helps to see how the quarter turn rotation yields (b). Another quarter turn of (b) yields (a) again.
Figure 19 Figure
20. Robert Longhurst: Arabesque XXIX (private collection)
Figure
20
Figure
21
Figure 22 Knots
frequently have symmetries from different viewpoints. These symmetries
help to hypersee the knot.
References [1] Eduardo Chillida, Basque Sculptor, Video, Home Vision, 24, 1985. [2] David Finn, As The Eye Moves, Harry Abrams, New York, 1968. [3] Linda Dalrymple Henderson, The Fourth Dimension and Non-Euclidean Geometry In Modern Art, Princeton University Press, 1983. [4] Phillip James, Henry Moore On Sculpture, Macdonald, 1966. [5] Howard Levine, See-Duction: How Scientists Are Creating a Third Way of Knowing Humanistic Mathematics Network Journal #15, 1997. [6] Joan Marter: Jos( De Rivera Constructions, Taller Ediciones, Madrid, 1977. |