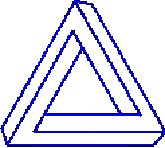
1. Introduction

Impossible figures are fascinating objects, related to art, psychology, and mathematics [1]. Lionel and Roger Penrose (father and son) introduced the impossible tribar in 1958 [2] (Fig. 1). A figure is called impossible when "a contradiction in our interpretation is noticed but does not result in our rejecting it in favour of a consistent one" [3]. The object represented in Fig. 1 is an impossible figure because our mind tries to interpret it as a three-dimensional (3D) object in the Euclidean space, with straight edges and planar faces, instead of interpreting it, for example, as a two-dimensional object drawn on the paper plane (which is perfectly possible).

Impossible figures have inspired researchers with more than one hundred papers (see Kulpa [4] for an extensive bibliography), and the Dutch artist Escher [5] with some famous drawings (see e.g. Fig. 2).

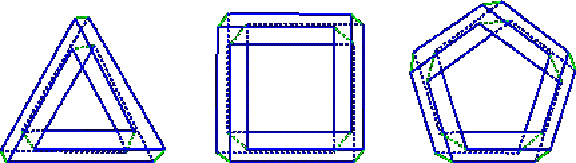
2. Multibars

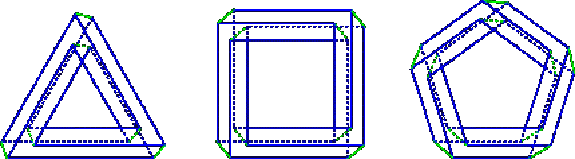
We define a multibar as a polyhedron [7],[8] that is any four-fold cover of a regular polygon. The first example is Penrose's tribar (Fig. 1), but other three-bars can be constructed as four-fold covers of an equilateral triangle. Some examples are shown in Fig. 3.

Intuitively, the two figures on the left seem impossible while the third one seems possible. We will now consider the family derived from the tribar of Fig. 1 (see Fig. 4).

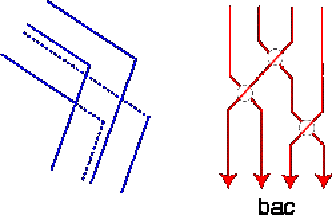
The first thing is to draw the hidden edges (Fig. 5)

It appears immediately that there are two kinds of edges: the longitudinal edges (drawn in blue) and the transversal edges (drawn in green). We were inspired by the work of T. M. Cowan [9],[10] who used braid theory to analyse impossible figures. He described each face of the impossible polyhedron by the string of a braid. We find more natural to describe each longitudinal edge of the impossible polyhedron by the string of a braid. Our aim is to show that braid theory is not sufficient to describe a multibar. The braid has to be closed into a knot or link in order for the multibar to have ony one representative.
 

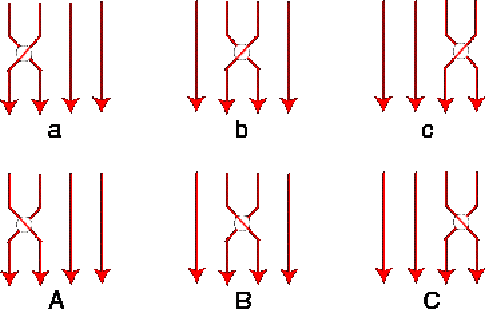
3. Braids

Let us introduce some basics of braid theory. A n-string braid consists of n strings going conventially from top to bottom. One string must never turn upside. The strings may cross each other and, at each crossing, the string passing behind the other is indicated by a gap. We use P. Dehornoy's convention [11] using lower-case and upper-case letters instead of s_i and s_i^-1 to designate the crossings (see Fig. 5).

 
 

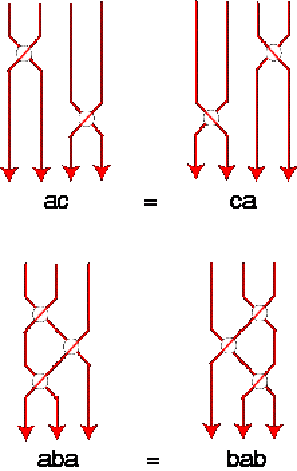
The braids form a group under concatenation, with the following relations (see Fig. 7).

The first relation (ac = ca) is valid for any two letters distant of at least 2 in the alphabet. The second relation (aba = bab) is valid for any two consecutive letters in the alphabet. One also have to take into account the usual inverse property of any group, i.e., aA = bB = cC = identity. The identity braid with n strings corresponds to n descending strings that don't cross.

Let us now look at one corner of a polyhedron of Fig. 5 (they all are identical). The corresponding 4-string braid is drawn in Fig. 8.

The 4-string braids corresponding to the tribar, the four-bar and the five-bar displayed in Fig. 5 are thus, respectively, bacbacbac, bacbacbacbac, and bacbacbacbacbac.

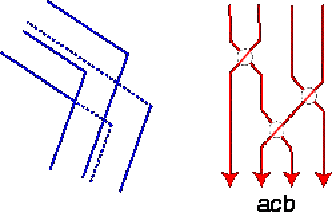
Now, we would like to draw your attention to the following fact. The polyhedra of Fig. 4 could as well have been drawn as in Fig. 9.

A corner of such a polyhedron would be represented by the following 4-string braid (Fig. 10)

 
 

The 4-string braids corresponding to the tribar, the four-bar and the five-bar of Fig. 4 would have been, respectively, acbacbacb, acbacbacbacb, and acbacbacbacbacb.
 
 

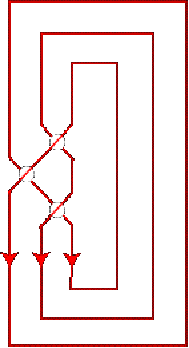
4. Knots and links

We now come to the closure of a braid, represented in Fig. 11. It gives rise to a knot (resp., link), that is, the embedding of one (resp., several) closed curve(s) in 3D space.

 
 

A theorem of A. A. Markov [12] states that different braids correspond to the same knot/link after closure if they are related by a finite series of two moves:

(i) conjugation (as is the case for the multibars we consider here: the b crossing is "moved" from one end of the braid to the other end along the closure),

(ii) move where a string is added together with a crossing between the last two strings. This move is off context here since the number of strings is fixed to 4.

We thus see that the multibars drawn in Fig. 4 have only one knot/link representative each, independently of the angle of view taken by the observer.

The superiority to the knot/link vision versus the braid vision is even more manifest when we consider the "magic pentagram" (Fig. 12, left), an impossible figure due to L. Sallows [13] and displayed on the last page of F. J. Swetz's book [14]. It is a four-fold cover of a pentagram and thus obeys our definition of multibar.

A 4-string braid representative of the magic pentagram would be bacbacbacbacbac or acbacbacbacbacb, thus undistinguishable from the five-bar of Fig. 4. On the contrary, the link corresponding to the magic pentagram is different from the link correponding to the regular five-bar since the embedding in the 3D space is taken into account. It is a satellite link [15] whose companion knot is the torus knot with 5 crossings (Fig. 12, right). Such a satellite link may not be trivial since its companion is a non-trivial knot.

On the countrary, if we draw (Fig. 13) the hidden edges of the three-bar of Fig. 3, right, which seems not to be an impossible figure, we see that the representative link is a trivial link with four components.

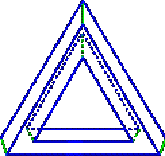
Fig. 13

We finally come to the following tentative criterion in order for a multibar to be an impossible figure: "If the knot or link corresponding to a multibar is different from the trivial link with four components, then the multibar is an impossible figure."
 

Acknowledgment

All my gratitude goes to Francis Buekenhout who made me discover the "magic pentagram" and who incited me to write this text.
 
 

References

[1] B. Ernst. Adventures with Impossible Figures. Tarquin, Norfolk, 1986.

[2] L. S. Penrose and R. Penrose (1958). Impossible objects: A special type of illusion. British J. of Psychology 49, 31-33.

[3] S. W. Draper (1978). The Penrose triangle and a family of related figures. Perception 7, 283-296.

[4] Z. Kulpa (1983). Are impossible figures possible? Signal Processing 5, 201-220.

[5] M. C. Escher. The Graphic Work of M. C. Escher. Ballantine Books, New York, 1971.

[6] The reproductions of Escher's drawings come from the following internet pages:

top: www.ex-cult.org/fwbo/fwbosection2.htm;

bottom: www.mgdesign.org/routeur_uk.php3?page=modelisation_uk.php3

[7] H. S. M. Coxeter. Regular Polytopes. Dover, New York, 1973.

[8] F. Buekenhout. Une Définition de Polyédre. Centre de Documentation Pédagogique, Université Libre de Bruxelles, Bruxelles, 2002.

[9] T. M. Cowan (1974). The theory of braids and the analysis of impossible figures. J. Math. Psychology 11, 190-212.

[10] T. M. Cowan (1982). Turning a penrose triangle inside out. J. Math. Psychology 26, 252-262.

[11] P. Dehornoy (1997). L'art de tresser. Dossier Pour la Science, La Science des Noeuds (avril 1997), 68-74.

[12] A. A. Markov (1936). Ueber die freie aquivalenz der geschlossenen Zopfe. Recueil de la Soc. Math. de Moscou 43, 73-78.

[13] L. Sallows (1995). The impossible problem. Math. Intelligencer 17, 27-33.

[14] F. J. Swetz (Ed.). From Five Fingers to Infinity; A Journey through the History of Mathematics. Open Court, Chicago, 1994.

[15] C. C. Adams. The Knot Book. Freeman, New York, 2001.