Abstract

In order to develop the taxonomy of a set of elements, the first step consists in identifying its component elements. For that end, first we have to define the term “Mathematical Sculpture”, a task somehow complex, as we will see. Then, we will develop the main objective of this paper: to present a classification of mathematical sculptures as exhaustive and complete as possible. We think that the best way for classifying mathematical sculpture consists in establishing general groups for the different areas of Mathematics and then subdividing these groups according to the main mathematical concepts used in the sculpture design. The main interest of this paper is to contribute to the study of Mathematical Sculpture so as to allow for its incorporation in higher education syllabi, either as a separate course or as a part of the course contents of other courses dealing with the relationship between Mathematics and Art.

1. Introduction

There are several studies on the topic of the so-called “Mathematical Sculpture”, a concept that we will try to define in the next section.

These studies deal with specific aspects, such as the mathematical study of the works of a particular sculptor or the analysis of a specific type of mathematical sculpture, or they are general studies. However, as far as we know, there is no work in the scientific literature that provides a systematic analysis of the possible relationships between Mathematics and Sculpture.

Neither is there any study that offers a complete and exhaustive classification of mathematical sculpture. The scarcity and lack of research studies on this artistic topic led us to choose it as the main objective of the doctoral thesis developed by Ricardo Zalaya, assistant lecturer at the Polytechnic University of Valencia, and tutored by Javier Barrallo, professor at the University of the Basque Country, Spain.

Figure 1: Sculpture located in front of Picasso Tower. Madrid, Spain.

In this paper we present an approach for the classification of Mathematical sculpture, based on the results of our research in the last years and on the comments and observations provided by other experts on the topic. This approach was presented at the Alhambra ISAMA-BRIDGES 2003 Meeting. The title of the paper presented at the meeting was Mathematical Sculpture Classification, quoted in reference [1].

At the Meeting, reference [2], the International Congresses of I.S.A.M.A (The International Society of the Arts, Mathematics and Architecture) and BRIDGES (Society for the promotion of "bridges" between Mathematics, Arts and Music) were held simultaneously. These two associations include some experts in the field of the relationship between Mathematics and Arts.

Mathematical sculpture works can be found in many places of the city, in addition to museums and exhibition halls. Figure 1 shows a simple sculpture which presents an interesting geometrical figure formed by thin cylindrical metal tubes. The design of this sculpture presents different concepts relative to Geometry and Topology: its surfaces (cylinders) and intersections, symmetries, closed loops, etc. Geometry is the Mathematical area more widely used in this kind of sculpture.

Here below we have included two works of a well-known mathematical sculptor, John Robinson, that clearly illustrate the mental process of abstraction and subsequent geometrization. Figure 4, shows an example of a more complex work by Bathsheba Grossman. Its design reflects several mathematical concepts: polyhedral geometry, surface topology, spatial isometric transformations.

Figure 2 (left): John Robinson, “Acrobats”.

Figure 3 (right): John Robinson, “Elation”.

Most researchers and experts in mathematical sculpture come from the United States of America, where this type of sculpture has gained great importance. Although in some West European countries, like Great Britain, and in other countries, like Japan, we can also find high quality artists and experts on this topic. Among them is Carlo Sequin, a professor at Berkeley University and a worldwide well-known expert. His webpage, included in the references, is an excellent tool for analyzing it.

Figure 4: Bathsheba Grossman, “Metatrine”. Metal.

2. The Concept of Mathematical Sculpture

In the first place and prior to any attempt for classifying the sculptures, we have to determine which kind of sculpture we are trying to typify, i.e., what we have called "Mathematical Sculpture". For that end, we propose the following definition: all the sculptures for which the application of Mathematics becomes essential in their conception, design, development or execution will belong to this typology. In order to include a given work in this typology, some mathematical concept or property must be significantly essential.

In this definition we include from the simplest geometry to the most complex non-Euclidean geometry. As can be noted, the definition proposed is very general and covers a wide spectrum of possibilities, as can be observed by looking at the different examples analyzed here.

Figure 5: Andréu Alfaro, “Ruled Surface”. Metal. Valencia, Spain.

Figure 6: Charles O. Perry, “Eclipse”. Welded metal. 13 m. The Hiatt Regency, San Francisco.

As an example, we present two sculptures based on the same concept, that of ruled surfaces, that is, the surfaces formed by joining the positions obtained by moving a straight line in space However, the complexity of both sculptures is clearly different. The work shown in figure 7 is very simple whereas the sculpture shown in figure 8 is very complex. The latter sculpture is an extension of the concept of ruled surface, to the use of the movement of any curve for the formation of the surface.

This sculpture has been made by one of the most complete mathematical sculptors, Charles Perry. To analyze his work consult reference [4], written by this sculptor, and researcher. The paper was presented at other international meetings on the relationship between Mathematics and Art, Mathematics & Design.

If we pay attention to the types of sculpture included in our proposal for classification, the design of mathematical sculptures makes use of concepts relative to many mathematical fields: Geometry, Differential Calculus or Vector Calculus, Algebra, Topology, Logic, etc.

This study can be faced from the common mathematical point of view, as can be appreciated in the group of sculptures by Javier Carvajal in reference [5], called . In this book, a Spanish expert on the relationship between Mathematics and Art, Eliseo Borrás, summarizes his research on the mathematical processes used in the design of these Javier Carvajal’s works.

Figure 7: Javier Carvajal, series: “Parallel Slices”. Case of 75º of section and 180º of total turn. Front view.

Figure 8: Javier Carvajal, Side view of the same sculpture.

An example of this is the sculpture is the work presented in figures 7 and 8. Figure 9, include another work of this sculptor, from his series called “Solomon Columns”. This illustrates the difficulty of delimiting the concept of mathematical sculpture and whether a particular work may be considered as a mathematical sculpture.

Note that some sculptures explicitly show this mathematical nature; an example of this could be the figure of a polyhedron; however, in other works these concepts are only present in an implicit or hidden way, such as the composition shown in figure 9, in which the mathematical conception is implicit in the sculpture's design.

The process of designing the sculptures begins with the obtaining of the bodies by sectioning a cylinder, see figure 10 at the bottom of next page. Each section is an ellipse whose position can be characterized by the angle, , that forms its main axis with the central axis of the cylinder (see picture on the left side of Figure 10). The plane determined by these two axes will be referred to as main plane of the section. Two different sections of the cylinder (right hand picture in Figure 10) will determine one construction module for these sculptures.

In addition to the respective angles, ₁ and ₂, the relative position of both sections is determined by angle f . Distance c is the distance between the centers of both ellipses. If c is sufficient to prevent the section from being cut, the module obtained is a "slice" (see picture on the right side of Figure 10). If the sections are cut, the two modules obtained are "segments" (central picture).

In a cylinder of known radius r, the set formed by the four parameters (₁, ₂, f , c), determines each of the modules that can be obtained using this procedure. It must also be fulfilled that angles ₁ and ₂ lie between 0° and 90° (included), and angle f, between 0° and 180°. These values indicate that theoretically we can give an infinite number of values to each of these four parameters.

If we place one module beside another module, by rotating them with an angle a, and orienting them in the same direction or reversing them, and with equal or different radius, new figures are formed that can be used by the sculptor in his works. Examples are ovoids, spheres, pumpkins, Solominic columns, torus, cones and swirling blades, etc. This angle a is then a new parameter. The movements of translation and rotation of the modules generate shapes that frequently are similar to the geometrical figures found in nature.

But not all shapes impact our senses in the same way. Some figures are more attractive than others and correspond to different “numerical rhythms”. Some of them, used in the sculptures by Javier Carvajal, are number p, which is present in the turnings. For example, this sculptor uses "polygonal spirals". In the figure of a polygon with n sides, after k turnings, its side will be:

Figure 9: Javier Carvajal, “Two columns of inverse rotation”. Series of sculptures: “Solominic Columns”. 1991-1994.

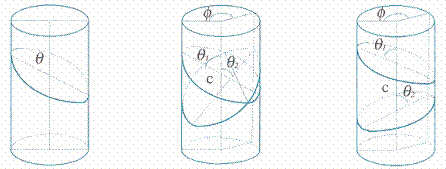
Figure 10: Sections of the pieces obtained from a cylinder and used by Javier Carvajal. Previous series of sculptures.

Figure 11: Javier Carvajal, “multipolygonal spirals”. Series . Spain, 1991-1994.

This supposes that the corresponding area is k² triangular units of the grid on which it is constructed. In the case of “Solomon columns” (Figure 9) there are 2p /a modules (Cylinder sections) with each turning and a length, measured from the center, of 2p c /a; thus, the lower the value of a, the higher the column.

In another type of sculptures made by Javier Carvajal, "multipolygonal spiral”, (see figure 11), the angles between the sides follow the relationship:

In its vector radii, the harmonic series is:

Since the main objective of this paper is the classification of Mathematical sculpture, the approach presented here will be different; we will try not to use the conventional mathematical language, based on a complex algebraic formulation. In this Instead, such kind of language will be replaced by images and photographs of the sculptures and by the graphical representation used in the design of the works.

The use of the computer by many sculptors has allowed the development and evolution of mathematical sculpture. In addition, the computer has allowed the correct execution of very complex sculptures. An illustration of this can be seen in Figure 12, which shows a work by Bathsheba Grossman with a very complex geometry.

Another example is the work made by the professor, computer expert, Javier Barrallo, one of the authors of this paper. The combination of such professional activities occurs in some of the artists involved in this working field. Figure 13 shows a "virtual sculpture" from his series “Hypersculpture”. Javier Barrallo uses the theory of fractals (see reference [6]). In a lecture (reference [7]) he analyzes this artistic field.

Figure 12: Bathsheba Grossman. “Seven spheres”.

Figure 13: Javier Barrallo. Virtual Sculpture of the series entitled “Hypersculpture”. 1994.

3. Purpose of classifying Mathematical Sculpture

The main objective of this research work, included in the doctoral thesis developed by Ricardo Zalaya, was the exhaustive historical analysis of the relationships between Mathematics and Sculpture and the proposal of a taxonomy for the classification of Mathematical Sculpture.

The educational purpose of classifying mathematical sculptures is to provide a more systematic approach in this field, so as to facilitate its incorporation in higher education. Courses devoted to the relationship between Mathematics and Art are already being included in the course contents of artistic and technical study syllabi, such as in Architecture.

We believe that without a classification like this, its analysis will be less structured, and will be restricted to the enumeration of a number of works or authors, based on specific studies. Examples of studies devoted to a particular sculptor are references [3] and [4], which analyze the work of John Robinson and Charles Perry, respectively. Other studies can be found in references [9] and [10], written by another mathematical sculptor, George Hart, about two particular types of his sculpture.

Figure 14: Brent Collins. Photograph of his workshop with several wood sculptures.

Figure 15: George Hart, “Fire and Ice”. Oak wood and bronze. 1997; diameter 60 cm.

4. Other approaches for the classification of Mathematical Sculpture

The only approach to classify Mathematical sculpture we know is based on the construction materials used, since they confer the works some geometrical properties. However, this typology does not permit to include all types of works. The different types are:

· Wood. This material is used to emphasize the curved surfaces of the work. See Figure 14, a photograph from Brent Collins' workshop, with sculptures in carved wood. Due to its lightness, wood permits to create works, otherwise unstable (figure 15 by George Hart).

· Welded metal. It is commonly used in sculptures consisting of polyhedrons. An illustration of this can be Bruce Beasley's work (figure 17).

· Concrete. It confers the works some common properties with Architecture. A characteristic sculptor is Eduardo Chillida whose work is shown in figure 22.

· Stone. This material also tends to emphasize the curved surfaces. As a result of their great weight, the works cannot be very complex. Nathaniel Friedman's works are made of stone (Figure 16). This work could be used as an illustration of the kind of works difficult to classify as Mathematical sculpture.

Figure 16: Nathaniel Friedman. ·”Grand Canyon”. Sculpture in Stone.

The type of typology that we propose is based on mathematical properties. The first approach for classifying mathematical sculpture in July 2003 was the result of the previous research The groups included in this first classification were defined by a geometrical or mathematical property or concept, or by a combination of both, that characterized the different sculptural works. The types considered in the first approach were:

· Classic and Polyhedral Geometry

· Non-oriented Surfaces

· Topological Knots

· Quadric and Ruled surfaces

· Modular and Symmetric structures

· Boolean Operations

· Minimal surfaces

· Transformations

· Others

Figure 17: Bruce Beasley, “Intersections II”. 1991, Bronze. Height: 3.55 m

As can be noted, some of the groups of this classification cover a wide range of sculptures. For example, the classic and polyhedral geometry group includes works with very different properties. However, other groups included in this taxonomy, for example that of minimal surfaces, are more restricted.

5. A proposal for the classification of Mathematical Sculpture

The reason why we have only presented the list of groups included in our first approach for classification, is because we think that this first approach has been improved in the final proposal presented in detail here below. This new classification is based on the different areas of Mathematics. The limits between the different groups included in the classification are not very strict, which is not surprising since the division of Mathematics into different "parts" is sometimes not so clearly defined. Our final proposal is the following:

· Sculpture with Geometric Characteristics

¨ Polyhedrons

¨ Curved Mathematical Surfaces

§ Quadric and Revolution Surfaces

§ Ruled Surfaces

§ Non-oriented Surfaces

§ Minimal or Zero-Mean Curved Surfaces

¨ Other Surfaces

· Sculpture with Algebraic concepts

¨ Symmetries

¨ Transformations and Modular Sculptures

¨ Boolean Operations

· Topological Sculpture

· Sculpture with different Mathematical Concepts

Figure 18: Bathsheba Grossman, “Alterknot”. Bronze and black marble. Size 13 cm.

This approach can be improved. For that, we expect to count with the collaboration and suggestions of mathematical sculpture researchers and sculptors. In some cases, the inclusion of a particular work in one of the groups of the classification proposed here may be difficult. A clear example of this is figure 18, a work by Bathsheba Grossman.

Some mathematical concepts are used in several mathematical areas, for example, symmetries, which means that some works can fall simultaneously into different groups or types. That is the case of the previous work, figure 15, by George Hart, which could be included in the Polyhedron type, within the group of Sculpture with Geometric Characteristics, and in the Symmetries and Modular Sculptures type, within the group of Sculptures with Algebraic Concepts. A paper of the sculptor, reference [12], describes the process of creation of this sculpture.

In this approach some of the groups still respond to mathematical concepts that, even when they are not very important or are not so widely used as others, offer a great potential to Sculpture, and have contributed to the design of a great number of high quality works.

Figure 19: Helaman Ferguson. “Minimal Surface Costa X”. Snow.

Figure 20: Tony Smith. “Amaryllis (plant family)”. Size 350 x 129 x 350 cm. 1965, Wadswhorh Atheneum, Conneticut, USA.

Some examples of this are the application of minimal surfaces or zero-mean curved surfaces (figure 19, a sculpture by Helaman Ferguson), and non-oriented surfaces (figure 21 by Brent Collins). As have mentioned, some works will include different mathematical concepts. An example can be seen in figure 18, a work by Bathsheba Grossman. In this work we can observe different concepts relative to mathematical surfaces, topological knots, symmetries, etc.

Therefore, we think that it is not possible to develop a strict typology for mathematical sculpture. This fact is evident in some of the examples shown in previous figures. We will try to classify each work according to its "dominant characteristic". This seems to happen in most works, which then can be included in one of the groups of the classification. We explained in detail at the reference [1].

6. General description and examples of works for the different types in the classification proposed here

In this section we will present a general description of the different groups mentioned in the classification, giving examples to illustrate their main characteristics.

6.1 Geometrical Sculpture

This is the widest group in the classification, as a consequence of the relationship between plastic arts, specially Sculpture, and Geometry. This kind of classification is so general that it could include most of the mathematical sculpture. To verify this, it will suffice to look at the photos shown in figures 1, 3, 5, 6, 7, 9, 11, 14, 19 and 20, which could all be included in this group.

There are examples of works which have made use of almost all possible types of solids, from the simplest ones like cubes, spheres, cones, cylinders, prisms, etc., to the most complex solids, like irregular polyhedrons or surfaces defined by highly complex mathematical equations. In addition, in some works the most relevant element is not a particular type of solid or a combination of them, but some property or properties, like a curved surface, etc.

Figure 21: Brent Collins. Non-oriented surface.

This important group in the classification includes from simple shape sculptures, for example the work in figure 20 by the sculptor Tony Smith, to much more complex works, for example the work shown in figure 6, "Eclipse". The same happens with size; it can range from very small sculptures, see figure 18, with only 13 cm in height, to huge dimensions, for example the13 m-high work "Eclipse".

Geometrical Sculpture is the type of mathematical sculpture with a greater tradition, specially in the 20th century. There are many works that can be included in this group. By the beginning of the century, in the Cubist Movement we find some works that can be included in this group. With respect to its origins, see the study about the background of Mathematical Sculpture, reference [8], that includes works of artistic trends and movements of the last century. Some authors belonging to the Abstract, Minimal and Conceptual movements, etc., made use of Geometry.

Figure 22: Eduardo Chillida, “Elogio del horizonte”, Gijón, Spain.

Polyhedral Sculpture. It is the first type included in the group of Geometrical Sculpture. The first polyhedrons analyzed will be Platonic Solids. This kind of solids is one of the geometrical figures more widely used by mathematical sculptors and by many other artists due to their beauty and simplicity.

Although their description is well-known, it is worth mentioning some characteristics of these regular polyhedrons. A convex polyhedron is regular if it is limited by regular polygons of a single type and if the same number of aristae converge at each vertex. There are only five solids of this type, known as Platonic (after the Greek geometrician and philosopher Plato) or cosmic. These five solids are: tetrahedron (4 sides); hexahedron or cube (6 sides); octahedron (8 sides); icosahedron (20 sides) and dodecahedron (12 sides).

Figure 23: Helaman Ferguson “Escher on Double Torus”. Alabaster, 6 inches, 15 cm.

In the same way as the Platonic polyhedrons, the truncated polyhedrons have been the source of inspiration of many mathematical sculptures. The possible cases of this type of polyhedrons are infinite. In addition, if the sides converge at every and each of the vertices of a regular polyhedron, they cut each other in such a way that the resulting plane sections are regular and congruent, and the rest of the solid is a new polyhedron known as semiregular or Archimediane. These have also been widely used in sculpture.

Another type of figures commonly used by mathematical sculptors are those resulting from transformations on the polyhedrons, such as deforming, star-shaping or rounding their sides, or any other geometrical transformation that may result in aesthetic effects. Figure 24 shows a work by John Robinson, based on a dodecahedron. Its sides have been replaced by 5-point stars. This work also presents other aesthetic values, like its color, or light reflections depending on its illumination, etc.

Figure 24: John Robinson, “Star Burst”. Year 1996. Stainless steel. Size 38 cm.

Figure 25: Francisco Sobrino, “Permutational Sculpture”. Size 250 x 150 x 150 cm. Stainless steel sheet, modules of 50 x 50 cm. Pyramidal base of 150 cm.,Valencia.

Figure 25 shows a work by Francisco Sobrino, consisting of a single module of stainless steel square sheet. These two works are perfect mathematical works. Some of the photographs presented in this paper also illustrate other examples of polyhedral sculpture, like the works corresponding to Figures 3, 15, and 22.

Mathematical Curved Surfaces forms the following type of the classification within the general group of Geometrical Sculptures; this type has been sub-divided into other non-excluding types. For example, a commonly used surface in Art is the hyperbolic paraboloid, also called saddle, which is a quadric and a ruled surface simultaneously.

Quadrics are surfaces defined by a two-degree (at most) algebraic equation, in the three variables. Non-degenerated quadrics are: spheres, cones, cylinders, ellipsoids, hyperboloids (with one or two sheets) and paraboloids (elliptic and hyperbolic). An example is shown in figure 26, with the title “Transformer”, by Aaron Fein.

Figure 26: Aaron Fein. “Transformer”, detail.

Figure 27: Carmen Grau, “Couple”. Size 285 x 150 m. Year 2000, Campus of the UPV, Valencia.

Figure 28: Max Bill, “Endless surface”. From 1953 to 1956. Size125 x 125 x 80 cm. Open air Sculpture Middlelheim Museum, Antverpen, Belgium.

Non-oriented Surfaces. Unlike the surfaces mentioned above, they are characterized by a concept of vector calculus, that of orienting surfaces. The simplest surface is Moebius strip, one of the first objects of this kind that appeared in sculpture. A pioneer of mathematical sculpture, Max Bill, extensively used it, obtaining very beautiful works, like the sculpture shown in Figure 28. With respect to the analysis of the mathematical characteristics of this author's works, it is interesting to read reference [12], by the researcher Ton Marar.

Another mathematical sculptor, Brent Collins, has developed many different models of non-oriented surfaces. One of his works can be seen in Figure 21. Also the Japanese sculptor Keizo Ushio has based some of his works on Moebius strip, and on extensions of this concept, creating very simple though splendid sculptures. In figure 30 the sculptor has used "a transformation of Moebius double strip". This figure clearly illustrates the "non-orientation" of the surface.

Figure 29: Charles Perry, “Hyperbolic Maze”.

Figure 30: Keizo Ushio, “Mihama”. Granite, 2 m. Year 1990.

Revolution Surfaces that, as their name suggests are formed by rotating a curve around any of its axes. They have been widely used in art, pottery, and in Sculpture. An example of its application is the simplification of human figures into two revolution surfaces, like in the sculpture “Couple”, by Carmen Grau (figure 27).

Ruled Surfaces are generated by displacing a straight line along a curve. This kind of surfaces has also inspired many artists and architects. Observe figure 29, by Charles Perry.

Minimal Surfaces, that is, zero-mean curvature, are local-area minimizing surfaces, resulting from the fact that it adopts the minimum value form of the possible area for the given boundary curve. A well-known example is that of the surfaces formed by soap films. Sculptor Helaman Ferguson has created different works based on this concept, see figure 20. This work is based on Costa surface. Its name comes from the Brazilian mathematician Celsoe Costa, who formulated its equations. For more details, see reference [13], by Carlo Sequin. Another example is figure 31 by Stewart Dickinson.

Other surfaces. This group includes those surfaces that do not belong to any of the specific types of surfaces mentioned above. In this group we can include sculptures with simple shapes, like planes, for example the sculptures by the sculptor of the Minimalism movement, Richard Serra, and sculptures with very complex shapes or works formed by the combination of different types of surfaces.

Figure 31: Stewart Dickinson. “Enneper’s minimal surface”.

Figure 32: Richard Serra. Set of works exhibited in Guggenheim Museum, Bilbao.

Figure 32 shows a photograph of Richard Serra's exhibition. His works present simple geometrical shapes, planes, ellipses, truncated cones, etc. One of his most famous works, “Snake”, shown in the central image, is based on a third-degree polynomial equation. In this group we can also include those works that adopt forms of surface equations not considered in the other groups. For example transcendent mathematical equations, such as trigonometric or exponential, etc.

6.2 Sculpture with Algebraic Concepts

This second general group of the classification comprises sculptures that make use of some algebraic concept in their design. These works can also adopt some of the geometric figures included in the other types of sculpture, but if the algebraic property is the dominant aspect in the sculpture, then we have classified it within this group.

Figure 33: Robert Longhurst, “Arabesque”.

Figure 34: Michael Waren, “Pascua”. Size 500 x 77 x 65 cm. Bronze. Year 2000, Campus of the UPV, Valencia.

Sculptures with Symmetries. One of the properties with more applications in Art is symmetry. Figure 33 illustrates a work by Robert Longhurst, which shows symmetry with respect to the planes whose angles are multiple of sixty degrees.

Transformations and Modular Sculptures. In other cases, the work will consist of a number of simple mathematical solids, like prisms or simple polyhedrons, to which some kind of algebraic transformation, such as translations, rotations, etc., has been applied.

To this group of Transformations belong the works by Javier Carvajal. As we have already mentioned, the design process of these works is based on obtaining the sections of a cylinder that subsequently are joined to create the complete sculpture, following different processes. Examples of sculptures by this sculptor are shown in figures 5, 9 and 11.

Modular Sculptures are those sculptures in which a given pattern is repeated; the modules thus formed can present very different figures. Brent Collins, the well-known mathematical sculptor, has also created modular sculptures, like those entitled “modular spirals”. Figure 34 shows a work of this type by another sculptor, Michael Waren.

Boolean Sculpture. Other sculptures are created using diverse operations with the shape of one or several solids, based on a specific algebraic structure, for instance, Boolean Algebra in this group. An example of this is the work by Bruce Beasley. A Boolean operation is the operation that fulfills the properties of Boolean Algebra. The possible results for these operations are two values: true or false. This applied to sculpture is used to describe how two solids relate, forming a new volume or emptiness. All logical operations are used: addition, intersection, inversion or search for the complementary, and exclusion. Figures 35 and 36 present two crosses by Eduardo Chillida. The first one can be interpreted as the complementary of its solid figure, that is, its "negative". The second cross, as if some parts had been excluded from the original block to form the figure.

Figure 35: Eduardo Chillida, cross of Santa Maria Church. San Sebastián, Spain.

Figure 36: Eduardo Chillida, cross of Buen Pastor Church. San Sebastian, Spain.

6.3 Topological Sculpture

Mathematicians have studied "knots" for many centuries. This interesting and fascinating category of topological objects presents a wide range of possibilities to be used in sculpture. Most mathematical sculptors have made use of this concept. The examples in figures 4, 9, 19 and 23 belong to this group. We include some more examples as an illustration of topological sculpture.

Figure 38 shows the computer image of the process followed to separate these two parts. The mathematical sculptor John Robinson has also elaborated many works that can be included in this group of the classification. These works are simple though interesting from the topological point of view. We present his series, called “Trilogy” (figures 40, 41 y 42 in the following page). In this case, he uses the same property as that of the Borromean rings, i.e., three embedded circumferences that cannot be separated. They are so called because in the Italian 15^th century, a family with this name used it as their family motto.

Figure 37: Keizo Ushio, “Oushi-Zokei”. (Sectioned Torus). Red granite. 120 cm. San Sebastián, 1999.

Figure 38: Images of the separation process into two parts of the sculpture in the previous image.

6.4 Sculpture with Different Mathematical Concepts

Although we improved our classification and included more groups it would be impossible to cover all types of mathematical sculptures. It may also be the case that one specific sculpture may fall into different groups because it does not show a unique "dominant" mathematical concept in its design. This happens in some of the works developed by the best mathematical sculptors, which combine different mathematical concepts and properties. A clear example is the work by Bathsheba Grossman, or the sculpture shown in figure 12.

For these cases we have established the last group of our classification. For example, figure 39 by sculptor Ken Herrick, has very little to do with the works presented in this paper; and the same happens with the two sculptures shown below. This heterogeneous group will also include those works characterized by novel concepts in mathematical sculpture, such as fractals, chaotic attractors, etc. Javier Barrallo, one of the authors of this paper, uses the theory of fractals in the design of his virtual sculptures. Figure 13 shows one of his works.

Figure 39: Ken Herrick, “Cloud ”. Metal and crystal.

Another example are some of the Helaman Ferguson’s works figure 43. Although it can also be included in the group of non-oriented surfaces, we believe that the characteristic texture of its surface is essential. That is why we have included it in this group. It was computer-designed, filling up the surface with a pattern obtained using a version of Hilbert's curve. Figure 44, “The Unit Cube”, by Bathsheba Grossman, is a cube, divided into two parts, which are complementary and fractal. If we ignore Pauli's exclusion principle, we observe that joining again the two parts, they form again the original cube.

Let us also mention the possibilities for mathematical sculpture of non-Euclidean, elliptic and hyperbolic geometries. The works generated using these new concepts should be included in this group. We firmly believe that the use of this type of geometries can be widely developed in sculpture, as it has happened in Painting. The typical example of this is the work by famous painter Maurits Cornelius Escher. Reference [14] studies a specific application of these geometries to sculpture. The paper was written by Irene Rosseau, who is also the author of the sculpture based on hyperbolic geometry shown in figure 45.

Figure 40: John Robinson, “Creation”. Series “Trilogy”.

Figure 41: John Robinson, “Intuition”. Series “Trilogy”.

Figure 42: John Robinson, “Genesis”. Series “Trilogy”.

Figure 43: Helaman Ferguson, “Umbilic Torus NC”.

7. Conclusions

This paper presents the results of our research work on mathematical sculpture and provides a proposal for its classification. The following conclusions have been sufficiently demonstrated or at least, have been sufficiently reasoned along this paper:

· There is a relationship between Mathematics and all the Arts. This relationship can even be extended to most artistic manifestations, taken in its broader sense.

· Sculpture is also related to Mathematics. This relationship becomes more evident in the sculpture developed in the 20^th century and at present time.

· The great advances in Mathematics in the Modern Age and Contemporary Age have made the development of a conceptually mathematical art possible.

· There is a kind of sculpture that can be considered conceptually mathematical. In this paper we have presented sufficient examples of sculptors who develop this type of sculpture, and of works which could be considered mathematical.

· Mathematical Sculpture has reached a significant status at present. The recent advances in Mathematics and computers have greatly contributed to this.

· We believe that Mathematical Sculpture will experience increasing importance, consequence of the reasons mentioned above as well as of the growing interest of artists and public.

· The inclusion in higher education of courses dealing with the relationship between Mathematics and Art should be fostered, specially in those syllabi relative to technical-artistic studies, such as Architecture. In fact, this is the case in some schools which are currently offering courses on these topics.

· It is possible to classify Sculpture using mathematical concepts. This classification will only be applicable to works of "Mathematical Sculpture". In this paper we have presented an approach for the classification of Mathematical Sculpture, as a first reasonable attempt to develop a taxonomy.

· The classification presented can be improved. We hope to improve the present proposal in doctoral thesis conclusions. There probably we will include some other mathematical concepts and properties not considered in this work.

· The development of a classification of "Mathematical Sculpture" of this type will allow its inclusion in the syllabi of higher education studies dealing with the relationship between Mathematics and Art.

Figure 44: Bathsheba Grossman, “The Unit Cube”. Silver.

Figure 45: Irene Rousseau, “Hyperbolic Diminution I”. Base of wood, covered with marble and glass mosaic.

8. References

[1] Zalaya Báez, Ricardo y Barrallo Calonge, Javier. Mathematical Sculpture Classification. Paper included in the Proceedings: Meeting Alhambra. ISAMA-BRIDGES 2003, pp. 53-60. Note reference [2.

[2] Several authors. Meeting Alhambra. ISAMA-BRIDGES 2003 & University of Granada. Proceedings of Conference, a joint celebration of the international associations: I.S.A.M.A and BRIDGES. Edited by Javier Barrallo, Nathaniel Friedman, Carlo Sequin and other and by Faculty of Sciences of University of Granada. Editorial: University of Granada; I.S.B.N.: 84-930669-1-5. Granada, 2003.

[3] Brown, Ronnie. Les escultures Simbòliques de John Robinson. Magazine: Mètode Universitat de Valencia. Number 37, Fons & Forma. Matemàtiques en la Creació Artística Actual. pp. 67-71. Editorial: Publicaciones de la Universidad de Valencia, 2003.

[4] Perry, Charles O. Mathematical Sculpture. Paper included in the Proceedings: Mathematics & Design 98, II Congress International. Edited by Javier Barrallo and by Department of Applied Mathematics, pp. 367-384. Editorial: Universidad del País Vasco; I.S.B.N.: 84-600-9459-6. San Sebastián, 1997.

[1] Carvajal, Javier; Moreno Gomez, Pilar, Borrás Veses, Eliseo and others. Forma y Número. Variaciones. Editorial: Fundación Bancaja; I.S.B.N.: 84-88715-47-I. Valencia, 1996.

[2] Barrallo, Javier. Geometría Fractal: Algoritmos y Creación Matemática. Lecture at: Cuartas Jornadas de Investigación y Fomento de la Multidisciplinariedad. Proceedings edited by Department of Applied Mathematics, pp. 89-95. Editorial: Servicio de Publicaciones de la UPV (Polytechnic University of Valencia); Depósito legal: V-3858-2002. Valencia, 2002.

[3] Barrallo, Javier. Matemáticas y Escultura. Lecture at: Terceres Jornades d´Innovacio Docente: Lénsenyament de les Matemàtiques i el Projecte EUROPA. Proceedings, pp. 3-10. Editorial: Servicio de Publicaciones de la UPV; Depósito legal: V-3857-2002. Valencia, 2002.

[4] Zalaya, Ricardo. Escultura Matemática: Antecedentes en la Historia del Arte y Clasificación por Conceptos Matemáticos. Research work of the doctoral thesis included in PhD: Multidisciplinary Mathematics of Polytechnic University of Valencia. Valencia, 2003.

[5] Hart, George W. Sculpture from Symmetrically Arranged Planar Components. Paper included in the Proceedings: Meeting Alhambra. ISAMA-BRIDGES 2003 & University of Granada, pp. 315-322. Note reference [2].

[6] Hart, George W. Zonish Polyhedra Paper included in the Proceedings: Mathematics & Design 98, pp. 653-660. Note reference [4].

[7] Colins, Brent and other. Whirled White Web: Art and Math in Snow. Paper included in the Proceedings: ISAMA-BRIDGES 2003, pp. 383-392. Note reference [2].

[8] Marar, Tom. Max Bill e a Matemática. Lecture at: Primera Jornada de Matemáticas y Arte, University of Valencia. Valencia, 2004.

[9] Sequin, Carlo H. Volution´s Evolution. Paper included in the Proceedings: ISAMA-BRIDGES 2003, pp. 13-24. Note reference [2].

[10] Rosseau, Irene. Geometric Mosaic Tiling on Hyperbolic Sculptures. Paper included in the Proceedings: Meeting Alhambra. ISAMA-BRIDGES 2003, pp. 127-133. Note reference [2].

1. Webpages

We just included webpages we have considered more interesting. Address or contains could changed. We specify them at June 14, 2004:

· http://www.cs.berkeley.edu/~sequin/

· http://www.sculptor.org/

· http://www.bathsheba.com/

· http://www.sckans.edu/~bridges/bcollins/bcollins.html

· http://www.helasculpt.com/

· http://www.asci.org/

· http://mitpress.mit.edu/

Acknowledgement: We would like to thank the Foreign Language Co-ordination Office at the Polytechnic University of Valencia for their help in translating this paper.