|
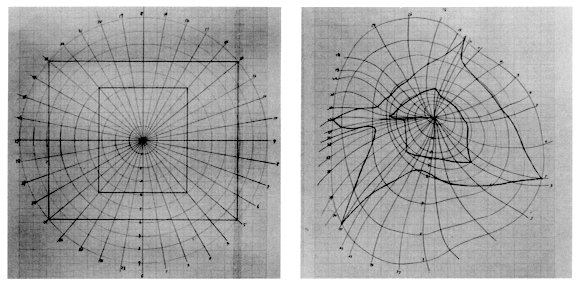
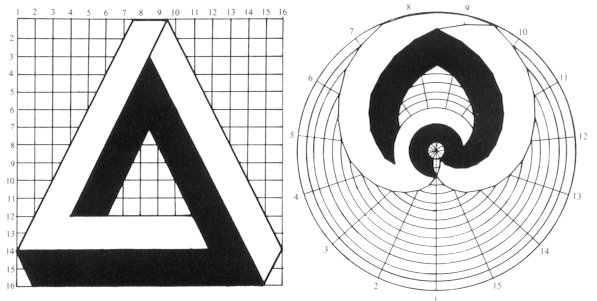
Next, points which correspond to these points are marked on the newly prepared unique coordinate lattice. Prepare many of these points, and finally those points are connected one after another. Then, the coordinate transformation of the configuration will be completed. We should pay attention to the following. When we try to transplant every point on the rectangular coordinates to the polar coordinates, inconsistency occurs. It is necessary that the points before and after transformation should have desirable relationships between both coordinates. We sometimes are not able to transform these diagrams. Therefore, before we start to work, it must be confirmed that there are the one-to-one or equivalent relationships between these points on these two coordinate systems. By the deformation of the concrete configuration due to coordinate transformation, a movement or an expression is sometimes vividly emphasized, or a humorous feeling is sometimes created by emphasizing a part of the configuration. In the case of the non-concrete configuration, it is interesting if an organized shape transforms into an unexpected shape. On the other hand, there is a problem in pursuing which kinds of coordinates should be used when a circle is made into a square, and a triangle is made into a star shape. It is also indeed interesting. It simply looks like explaining a puzzle, and practical values to be utilized are not clear. However, these kinds of experiments must be useful
in the future. Recently, not only transformations between plane shapes
but also transformations from a plane diagram to a solid diagram have become
possible by the appearance of computers. This is a great advantage of scientific
equipment.
|