|
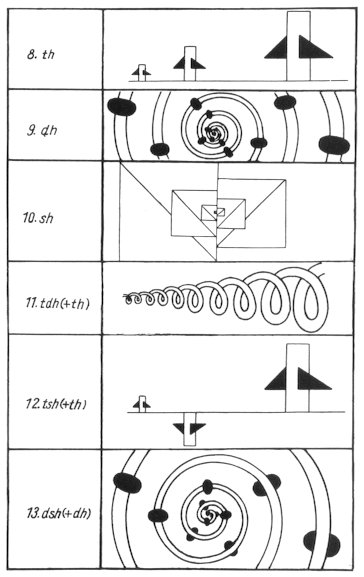
The etymology of the word of symmetry comes from Symmetria or Symmetrios in Greek or Latin which are the combination of sym (together) and metron (measure). In other words, it expresses the relationships that there are the same shapes at the same distance from a point. Therefore, the following symmetries are defined as follows: the rotational symmetry that a shape is exactly overlapping with other shape by rotating the shape around a center is defined, and the mirror symmetry that a pair of symmetrical shapes created by reflecting the shape on a mirror. The symmetries in one or two dimensions are included in the pair of shapes. The above two symmetries were taught in school. But recently, the translational symmetry that shapes are overlapping by a translational movement (translation: shift and movement of a shape) is usually added. There is a unique theory on symmetry as described in the book, "Symmetrie" by K.L. Wolf. (co- authored by K. Lothar Wolf, and Roben Wolf, Köln, 1956). Wolf stated here that "Streckung" is also one of the basic operations of symmetry. (The word "Streckung" is a German word which has meanings of extension or expansion. Here, it means an necessary operation of expansion or reduction of a shape to create similar figures.) Then, the fundamental operations for symmetriy will be the following four of "Translation", "Spiegelung", "Drehung", and "Streckung". Combination and simultaneous use of them will result in more than ten kinds of operations. In the category of Wolf, there are 13 kinds of them as shown in the tables below. In mathematics, the operation of "expansion or the
reduction" may or may not be added to the group of symmetries depending
on the ways of establishing conditions.
|