|
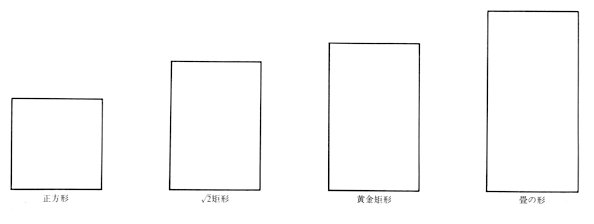
(2) Root rectangles The methods to obtain Ö2 and Ö3 are very easy even needless to explain as shown in Figures 236 and 237. The Ön which contains a natural number within the root can also be obtained easily as shown in Figure 239. Assuming AB=1, ABDD' is called a Ö2 rectangle here. Similarly, assuming AB=1, the rectangle ABEE' with another side of BE of the length Ö3 is called a Ö3 rectangle. A Ö4 rectangle is
a combination of two squares, and it looks a little longer. This rectangle
is widely used for example in the fields of constructions and interior
designs. Tatamis, bricks, blocks, and so on are frequently seen. In the
shape of bricks and others, the ratio of the short side and the long side
is not only 1:2 but also the ratio of the thickness and the short side
is 1:2. Therefore, when this shape is combined and used, it is very easy
to handle. Therefore, it is said to be a unit of a very rational shape.
The Ö2 rectangle is also rational. When
it is folded into the half, this shapes becomes a rectangle of the same
proportion as the original shape. In a word, the area is half, but the
same Ö2 rectangle shape is created. Therefore,
the rectangle is widely used as a size of the books and the newspapers
which are folded. The standards of the printing form are consistently determined
in many countries. In Japan, the Ö2 rectangle
is used as the proportion of the paper in Japanese Industrial Standards
(JlS) as well. The A system starts from the area of 1m2 (A0),
and it continues like 0.5m2 (A1), 0.25m2 (A2), and etc. The
B system starts from the area of 1.5m2 (B0), and it continues like 0.75m2
(B1), 0.375m2 (B2), and etc. Most paper products from
printed matters to notebooks and drawing papers employ this Ö2
rectangle systems. Therefore, we are living using or seeing the enormous
numbers of the Ö2 rectangles.
|
||||