
An animation of numbers 999...999n.
Daisuke Minematsu
Satoshi Hashiba
Ryohei Miyadera Kwansei Gakuin University.
We have presented a beautiful figure made of 999...9n and its theoretical background in Miyadera [1] ( Visual Mathematics , Vol 6, No.2, 2006 ).
Here we are going to show a beautiful movie made of these numbers.
You can appreciate the beauty of these numbers very much when we make a movie using them.
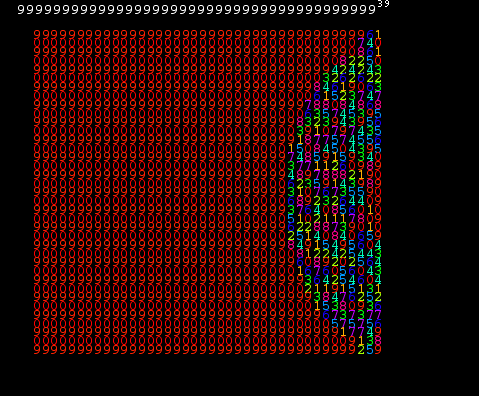
Example 1. We are going to study the numbers with the form of xy with x = 99...99 and an integer y.
We are going to make x bigger and y smaller while keeping the size of the number xy almost the same as the following table shows.

We are going to make a movie using these numbers xy in this table.
We express these numbers as matrixes whose length of row is 40, and color each numbers 1, 2, 3, 4, 5, 6, 7, 8, 9, 0 with different colors. We express all these numbers xy as 40×38 matrix by cutting off some part of the digits of these numbers. Then we can easily make a movie using these numbers.
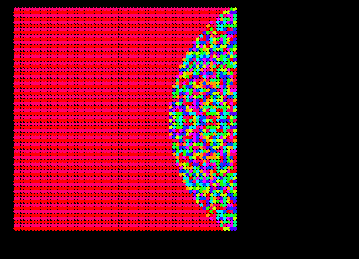
The movie starts with Picture 1, and ends with Picture 2. Please click the underlined text below to start the movie.
Picture 1.
 V
V
Picture 2.
Remark.
The figure in Picture 2 is almost identical to the graph of the function
y = - (Log10x + (1-x)Log10(1-x)), where the x-coordinate is vertical.
As to this fact see Theorem 1 in Miyadera, Minematsu and Hashiba [1].
The movie looks more beautiful when we use bigger numbers.
Example 2. This time we are going to make a movie using bigger numbers. We start with 99999902, and end with 99999999999999999999999999999999999999999999999999999999999999999968.
The movie starts with Picture 3 and ends with Picture 4. Please click the underlined text below to start the movie.
Picture 3.

Picture 4.
Remark.
The figure in Picture 4 is almost identical to the graph of the function
y = - (Log10x + (1-x)Log10(1-x)), where the x-coordinate is vertical.
References.
[1] R.Miyadera, D.Minematsu and S.Hashiba, A beautiful figure made of 999...9n, Visual Mathematics , Vol 6, No.2, 2006, Mathematical Institute of the Serbian Academy of Sciences and Arts.
http://www.mi.sanu.ac.yu/vismath/miyadera/999.html
[2] R.Miyadera, D.Minematsu and S.Hashiba, A beautiful figure made of 9999...999^n, Wolfram Information Center,
http://library.wolfram.com/infocenter/MathSource/6194/