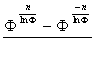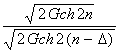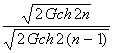DYNAMIC SYMMETRY IN NATURE AND ARCHITECTURE

Oleh Bodnar

Doctor of Art Studies, Professor of Lviv National Academy of Arts,

Lviv, Ukraine, 2010

Abstract

The phenomenon of dynamic symmetry in botanical, the so-called philotaxian, systems is investigated. A mathematical model of phylotaxis grounded on Minkovsky's geometry, as well as the original trigonometric apparatus based upon the golden ratio, are developed. Constant values of phylotaxis dynamic symmetry are defined. The principle of dynamic symmetry in architecture, formulated by D. Hambidge, as well as architect Le Corbusier's Modulor proportional system, are described in terms of philotaxis mathematics.

The term dynamic symmetry was for the first time applied by the American architecture researcher J. Hambidge to a certain principle of proportioning in architecture [11]. Later this term independently appeared in physics where it was introduced to describe physical processes that are characterized by invariants [10]. Finally, in the given research the term dynamic symmetry is applied to regularity of natural form-shaping that in terms of origin also appears not to be connected with Hambidge's idea, and, moreover, appearance of this term in physics. However, all the three variants are deeply interconnected in terms of their meaning which we are going to show.

At first, we point out strategic similarity of Hambidge's and our researches. This is a well-known historical direction which in the field of architecture and art is motivated by the search for harmony regularities and, thus, is aimed at studying the objects of nature. Usually architects take interest in the structural regularities of natural form-shaping and, particularly, in the golden section and Fibonacci numbers which are regularities standing out by their intriguing role in architectural form-shaping. It is not accidentally that architects who do researches so frequently pay attention to botanical phenomenon phyllotaxis which is characterized by these regularities.

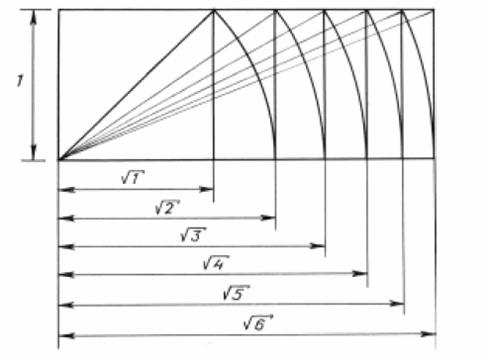
Phyllotaxis was the focus of attention of J. Hambidge who is the author of the first variant of the dynamic symmetry concept. While studying this phenomenon, J. Hambidge introduces a law of the so called uniform growth and suggests its geometrical interpretation - spiral of uniform growth or, in other words, - golden spiral (Fig. 1).

Fig. 1. Building the golden spiral according to Hambidge.

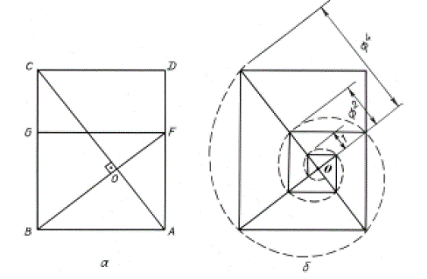
However, the most important generalization of Hambidge that resulted from his studying the regularities of natural form-building (phyllotaxis) as well as proportions of classical architecture comes to the idea of architectural proportioning that is called dynamic symmetry. J. Hambidge demonstrates it by means of simple geometrical scheme (Fig. 2).

Fig. 2. Proportional system «Dynamic symmetry» by J. Hambidge.

This successive system of rectangles the first of which is a square and the next successive one is built on the side of the original square equal to 7 and the diagonal of the previous rectangle. Thus, the series of rectangles is formed with the ratio of sides expressing the series . In this series Hambidge differentiates two types of rectangles - static and dynamic. Static rectangles have their side ratios expressed in integers while dynamic ones - in irrational numbers. According to Hambidge, dynamic rectangles express the idea of growth, motion and development. Among such rectangles he distinguishes three rectangles which long sides equal . However, he pays particular attention to the rectangle which is directly connected with the «golden rectangle» Hambidge conducts thorough geometrical research discovering various manifestations of the golden section in the system of rectangle . Studying the geometrical features of this rectangle he illustrates the possibility of applying it to the analysis of the proportions of classical architecture and art objects (Fig. 3, 4).

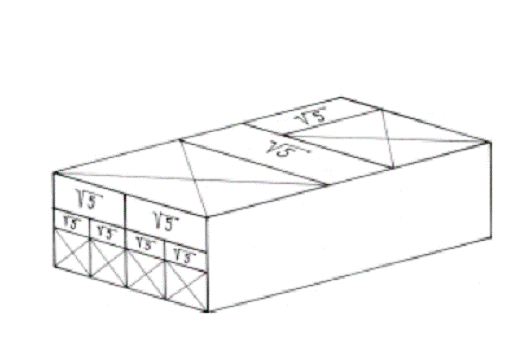
Fig. 3. Three-D model of Parthenon's proportions by J. Hambidge.

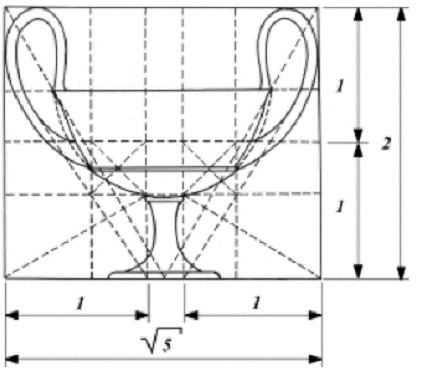
Fig. 4. Diagram of Greek vase (cantaros) proportions by J. Hambidge.

Thus, this is in brief the essence of J. Hambidge's idea of dynamic symmetry. As one can see, it does not directly derive from the phyllotaxis properties. Generally, J. Hambidge does not go deep in mathematics of phyllotaxis. In his various schemes illustrating the regularities of uniform growth or other ideas of proportioning he applies well-known numerical relations typical of phyllotaxis, including golden section.

However, his idea of dynamic symmetry is an original one and in terms of its mathematical content expresses regularities of quite a general character. It will be possible to demonstrate it after studying the phyllotaxis research offered below. But before I would like to predict some possible "unfavourable impressions" that the representatives of various fields of science may get after reading this text. The author foresees the possible dissatisfaction on the part of biologists due to schematic layout and insufficient terminology of biological description of this phenomenon; mathematicians - who may discover incompliance of symbolics with that used in phyllotaxis theory; art historians who may be faced with too much mathematical direction of the research from the viewpoint of art methodology. The author fully acknowledges all the "troubles" caused by the multidisciplinary character of the issue.

And still, the author takes on responsibility for the scientific credibility of the results achieved. The central task of the research is formulated on the basis of minimum initial information which is sufficient to grasp the essence of the main issue of the problem and build the research "from scratch" making it independent of the research experience accumulated in the field. Though, it is worth mentioning that this experience is quite substantial. The research of phyllotaxis was in the centre of attention of many mathematicians and biologists. For instance, in the second half of the 20^th century it was in the focus of interest of H. Cockster [7], Adler [12], Jean [13], Schwabe [14], Petukhov [9], etc. who in their works created the modern "mathematical and biological" theory of phyllotaxis.

The results of the given research were first published in 1989 [1]. At that time they were new. At any rate, none of the researchers describing phyllotaxis applied Minkowski's geometry and the system of hyperbolic trigonometry. We shall briefly describe this research.

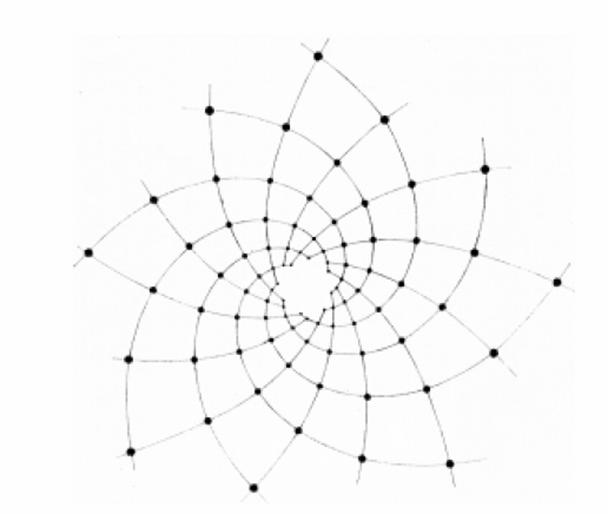
It is known from biology that mutual arrangement of various primordia that appear on the cones of spindles is characterized by the spiral symmetry. This principle of situation that was named phyllotaxis is also clearly observed in dense inflorescences and infructescences, for instance, on sunflower discs, pine cones and many other types of bioforms (Fig. 5).

On the surfaces of phyllotaxis forms, dense inflorescences and infructescences in particular, one can clearly observe left- and right-wound spiral-like rows of structural elements (primordia, seeds, leaves). The symmetry order of phyllotaxis forms is usually shown as the ratio of numbers that corresponds to the quantity of left and right spirals. According to phyllotaxis law these ratios are described by the combinations of numbers of recurrent rows which accept the rule: u _n = u _{n - 2} + u _{n - 1}. Widely spread are the symmetrical type of phyllotaxis which are described by Fibonacci series: …, 0, 1, 1, 3, 5, 8, 13, 21, 34, … . Numbers of Lucas series …, 1, 3, 4, 7, 11, 18, 29, 34, … are also quite frequently realized in phyllotaxis, seldom - numbers that belong to the series …, 4, 5, 9, 14, 23, … . The order of symmetry in case of Fibonacci phyllotaxis (F-phyllotaxis) is expressed by the ratios: , , , , , … .

It is typical that in symmetry cases always there are neighboring numbers of the series. In certain cases, when on the surfaces of the pattern one can single out three groups of spirals, the symmetry is shown by means of three numbers. As a rule, the off-shoots of plants and trees are characterized by the low order of symmetry while the inflorescences and infructescences - by high symmetry order. For instance, the order of symmetry with sunflower can be up to , and even .

The interesting indicator of phyllotaxis structures is the so called D divergence which is the angle of splitting of twosubsequent primordia. Divergence measured in circle fractions in case of F-phyllotaxis is always expressed by the same number that is the pattern order of symmetry, i.e. it can be equal , , , , , … . As it is known, this series of fractions tends to the limit » 0,618 of the circle, with which the full plane angle appears to be divided as to the golden section F.

Some types of phyllotaxis patterns while growing subsequently change (expand) the order of their symmetry. It is this peculiarity of phyllotaxis that we name dynamic symmetry. As an example, one can take the sunflower. The sunflower heads arranged on the various levels of one and the same stem have different symmetry: the higher the level, i.e. the older the disk, the higher its order of symmetry is. In symmetry dynamics the following sequence is realized:

… ® ® ® ® ® … .

With the change of symmetry the divergence angle changes respectively. Still on all the disks regardless of the number of spirals the so called conforming (angular) characteristics of spiral patterns appear to be the same, that is - the spirals cross at a straight angle.

This data is enough to identify the objective of the research. It means to geometrically decipher the phyllotaxis pattern formation process and the key issue is how the symmetry changes.

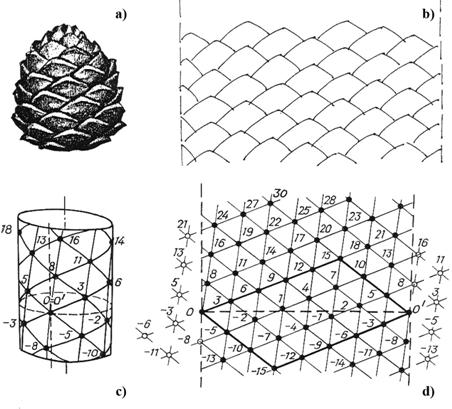
At the beginning it was necessary to do a simple geometrical stylization of phyllotaxis surface and represent it as a regular flat lattice (Fig. 4). This lattice (Fig. 6d) is numbered in such a way that the numbers of vertices characterize their distance from the straight line 00'; at the same time per unit is accepted the distance to the nearest from 00' point 1. Due to this numbering rule the order of symmetry of cylindrical lattice in the system of numerical denomination is expressed in the following way: points adjacent to 0 are numbered 5, 8 and 3 (also -5, -8 and -3), i.e. such numbers that characterize numerical structure of helical spiral of cylindrical lattice.

It is obvious that for the lattices with different symmetry the numbers of neighboring vertices of O point will be different.

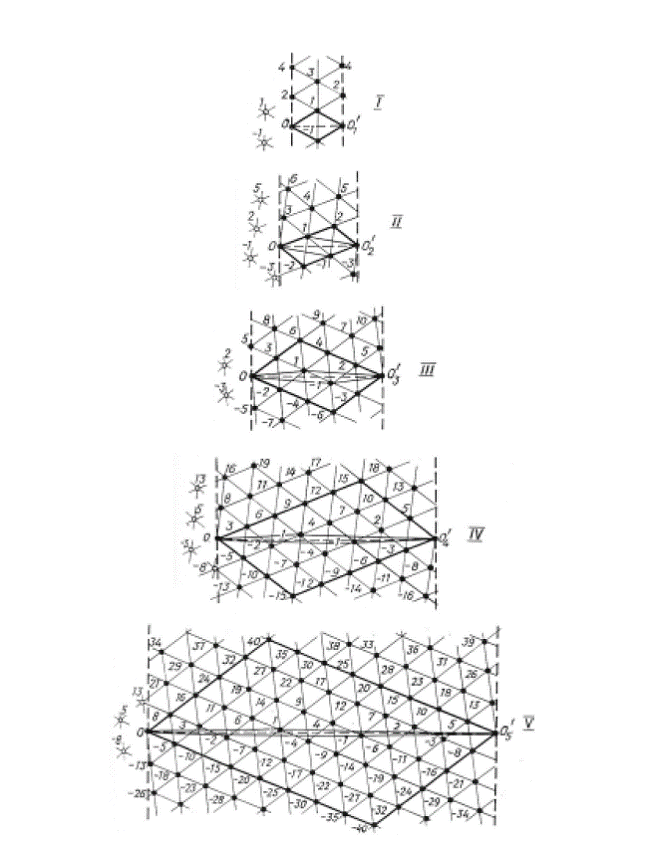
We shall do the comparative analysis of the series of lattices illustrating the sequential stages of symmetry change in phyllotaxis (Fig. 7). According to their metrical features, all the lattices are the same. Thus, the peculiarity of natural phyllotaxis lattices to renew their conforming characteristics at any stage of symmetrical development is taken into account.

It is obvious that for the lattices with different symmetry the numbers of neighboring vertices of O point will be different.

Movie installation No 1

Video 1

Fig.6. Analysis of structural and numerical features of phyllotaxis lattice:

a - general look of cedar cone;

b - scheme of unrolling;

c - cylindrical lattice - idealized form of cedar cone;

d - unrolling of cylindrical lattice

We shall do the comparative analysis of the series of lattices illustrating the sequential stages of symmetry change in phyllotaxis (Fig. 7). According to their metrical features, all the lattices are the same. Thus, the peculiarity of natural phyllotaxis lattices to renew their conforming characteristics at any stage of symmetrical development is taken into account.

Let us trace the regularity of transformation of parallelogram 010'. We shall start from the scheme ІІІ. One can see that the sides 01 and 0' of this parallelogram are equal to the sections 00'₁ and 00'₂, which are the diagonals of this parallelogram at the two previous stages of its transformation, i.e. at the stages І and ІІ. The sides of parallelogram 010'₄ at the fourth stage appear to be equal the sections 00'₂ and 00'₃. This regularity can be traced also at the next stages. Let us provide separate illustration of this regularity (Fig. 7)

Fig.7. The series of unrollings illustrating sequential stages of cylindrical lattices symmetrical transformation. All the schemes depict parallelogram OII'O'

Fig.8. Research of elementary parallelogram transformation regularities.

The building rule is that sides of every parallelogram (starting with the third one) are diagonals of two foregoing parallelograms. As any two successive parallelograms have three common vertices, it is obvious that all parallelograms have equal square. Preserving the square is the first interesting feature of parallelogram dynamic transformation. The second is that straight lines are parallel: parallelogram at any stage of transformation still is a parallelogram. Here one can draw the key supposition of the research - preservation of square and parallelism of straight lines are the features of hyperbolic rotation. It means we deal with hyperbolic transformation. It is necessary to specify this idea.

Fig.9. Transformation of elementary parallelogram by means of hyperbolic motion.

Fig.10. Scheme of lattice transformation by hyperbolic rotation.

.

Figures 9 and 10 illustrate "binding" of the lattice to the scheme of hyperbolic transformation.

Movie installation No 2.

Video 2

Thus, we can state that hyperbolic rotation is the basis of symmetry transformation illustrated on Fig. 7. This is the key finding of the research that allows to develop an entirely new look at the issue of phyllotaxis geometry.

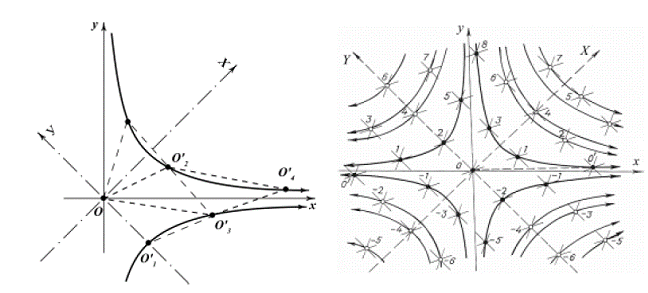
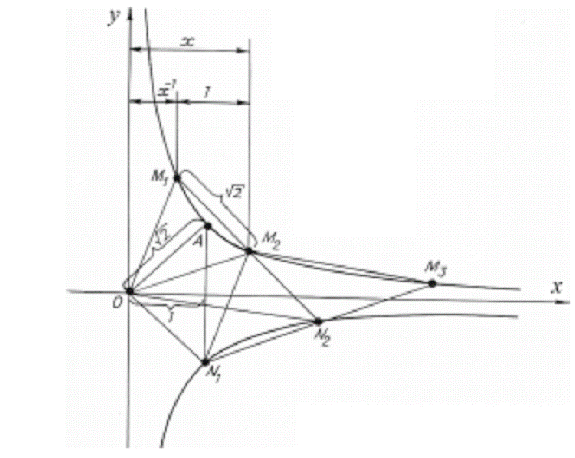
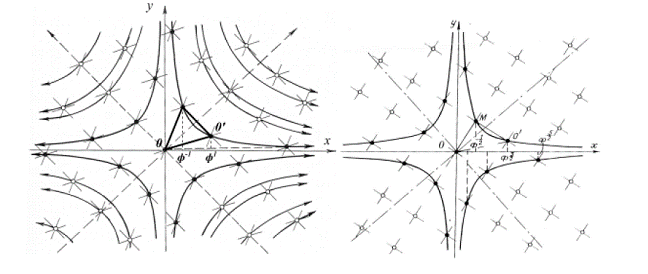
First of all, within the framework of the idea of hyperbolic rotation it is necessary to conduct a specific analytical and geometric research of a regular lattice. Immediately an interesting fact is revealed - in metrical characteristics of the lattice organically present is the value of the golden section. (Fig. 10).

Let us have a look at Fig 11. Here the arrangement of vertices corresponds to the Fig. 5.9, 5.10 and is characterized by the following conditions:

:

x_A = = 1, y_A = 1, 0A = 0N₁ = ;

points М₁ and М₂ are symmetrical as to 0А; 0М₁М₂N₁, 0М₂N₂N₁, 0М₂М₃N₂ are parallelograms, that means that 0N₁ = М₁М₂ = 0A = .

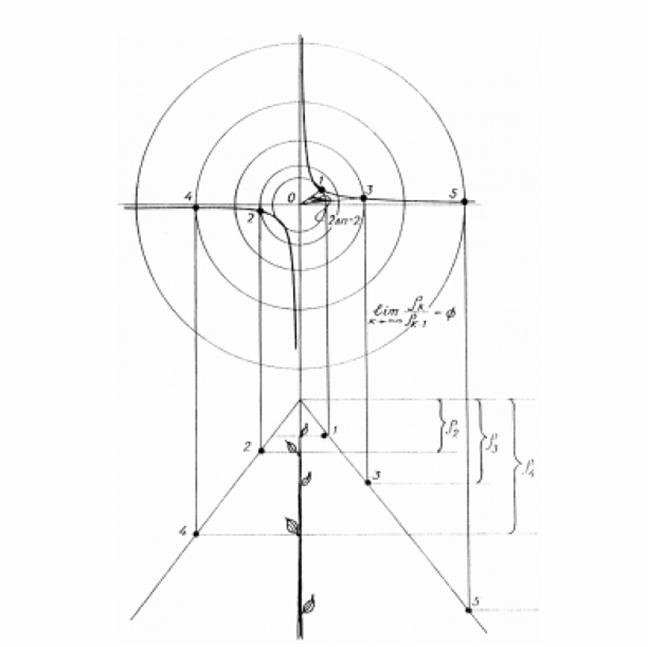
Fig.11. Analysis of lattice metrical features.

Let us determine the abscissa of the point М₂, marking = x. From the condition of symmetry of the points М₁ and М₂ it goes that = = x ^{- 1} and that the section М₁М₂ is tilted at an angle of 45^о to the axis 0х. It is evident that the difference of abscissas of the points М₁ and М₂ is equal to 1. We shall write down and solve the equation

х - х ^{- 1} = 1,

х² - х - 1 = 0,

х = .

As follows from the statement of the problem = = F. Now one can easily make conclusions. The coordinates x and y of the arbitrary lattice can be expressed in formula:

х = · F ⁿ, y = · F ^{- n}, (1)

where а - is the semi-axis of hyperbole that the point under consideration belongs to. Moreover, if for the angular unit (module) of hyperbolic rotation one takes the angle dividing two neighboring transformation stages (for instance, stages I and II, II and III, III and IV, etc. - Fig.7), in other words, the smallest angle, the rotation to which will result in the self-alignment of the lettice, then the exponent n will coincide with the value of hyperbolic angle (in modules), characterizing the position of the point under consideration (Fig. 12).

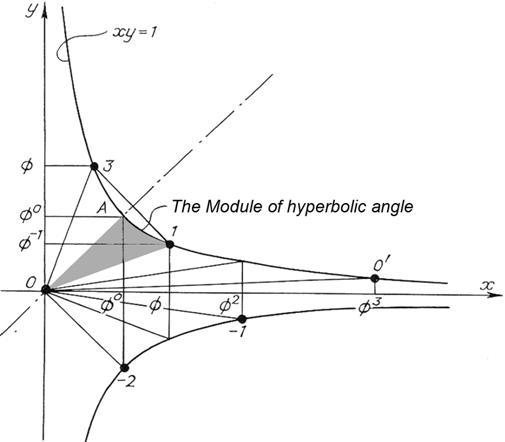
Fig.12. Determining the module of hyperbolic angle.

In the coordinate system X0Y the formulae of the coordinates of the arbitrary point look like hyperbolic functions:

X = a ·, Y = a ·. (2)

As one can see, these are unusual hyperbolic functions as both the base F and the value of hyperbolic angle unit here differ from the accepted ones*.

(* In classic variant hyperbolic angle unit is the square of the so called coordinate rectangular of the hyperbole point М, that is formed by the coordinate axes and the straight lines that were drawn through the point М in parallel to the coordinate axes. If the hyperbole equation is xy = 1, then the square of the coordinate rectangular is numerically equal to 1. If unit square pertains to the hyperbolic sector 0АМ (А - hyperbola vertex), then x_M = e, and y_M = e ^{- 1}.)

Therefore, these functions have independent signs and names:

for = Gch n - the golden cosine,

for = Gsh n - the golden sine,

for = Gth n - the golden tangent, etc.

The golden functions preserve the main features of the "classical" hyperbolic functions and accommodate with them taking into account the dependence between numbers F and е (F = e ^{ln F}, F ⁿ = e ^{n ln F},). For instance:

= , Gch n = ch (n · ln F);

= , sh n = Gsh .

Formulae (2) of the coordinates of the arbitrary point in the system X0Y now can be written like that:

X = a · Gch n, Y = a · Gsh n. (3)

Changes of arbitrary point coordinates caused by the hyperbolic rotation are expressed by the formulae:

x' = X · Gch n + Y · Gsh n,

y' = X · Gsh n + Y · Gch n. (4)

In the process of hyperbolic rotation the lattice is deformed, but periodically, through rotation module the same metric states are repeated.

Fig. 13 illustrate the subsequent deformation stages of the lattice elementary triangle which are fixed through half-module of the rotation. The metric peculiarities of the triangle are obvious. Fig. 14 show full lattice depictions in two extreme states. In one of them (Fig. 13) the elementary triangle gets the sizes , , , in the other (Fig. 14), when the lattice is getting square, the triangle becomes a 45 grad right triangle. These two states set the general lattice triangle deformation range.

Movie installation No 3.

Video 3

As one can see, the transformation of the lattice by means of hyperbolic rotation is characterized by periodicity. Two rotation modules are considered to make a full period (cycle). It is necessary to note that the lattice state is repeated through one module, however two such states do not coincide, they are in mirror position as to the hyperboles symmetry axes.

It is important to state: hyperbolic rotation is symmetry transformation of a regular lattice. This transformation is not considered in the classical theory of symmetry.

Fig.13. Characteristic conditions of lattice elementary triangle.

Fig.14. Two extreme conditions of the lattice.

It is also necessary to focus on the following issues. 1) Unlike the circular rotation when the lattice knots preserve strict mutual arrangement, the process of hyperbolic rotation leads to the changing of the mutual arrangement of the knots. 2). For the symmetric transformation the lattice should be placed onto the hyperplane in a special way. In general, the basic lattice lines should not coincide with asymptotes. Fig. 15 (as compared to Fig. 14) illustrates the effect of such "non-phyllotaxis" transformation. We shall not concentrate on this important point deserves separate consideration. Let us continue the research.

Fig.15. Transformation effect when asymptotes go through the lattice knots.

Following the principle of lattice numeration the number of any of its points in the coordinate system where abscissa axis coincides with the direction 00' (Fig. 6, 10), is numerically equal to its ordinate. We have developed formulae to describe the coordinates of arbitrary vertex in the system of movable coordinates x'0y' (Fig. 16).

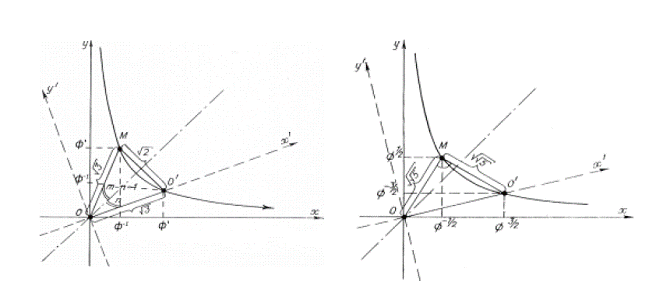
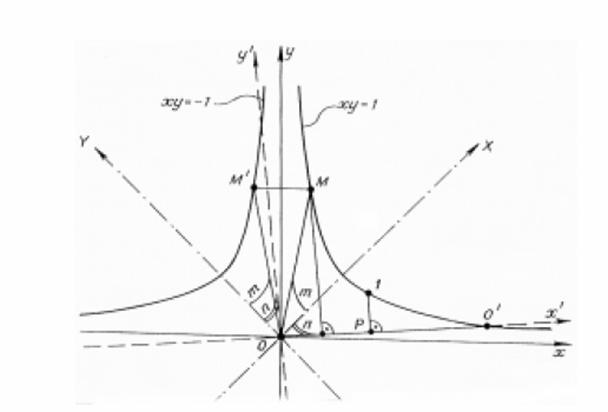
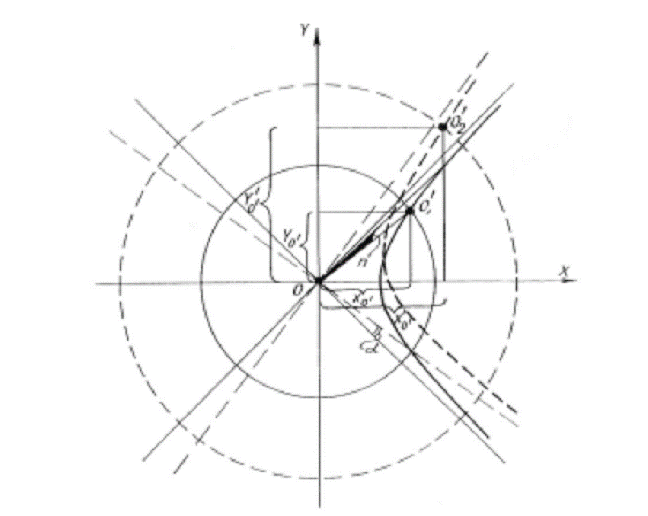
Fig.16. Determining coordinates of the arbitrary point in the system of movable coordinates X'oy'.

With any position of the coordinates the ordinate of the point 1 nearest to 0x' is taken as a unit of measurement. Thus, for vertices that belong to the hyperbole xy = 1, we have:

x'_M = · Gch (m - n),

y'_M = · Gsh (m + n), (5)

where m - hyperbolic angle X0M, n - hyperbolic angle X00'. For vertices that are situated on the hyperbole xy = - 1, the coordinate formulae will be the following:

x'_M' = · Gsh (m - n),

y'_M' = · Gch (m + n). (6)

Thus, in formulae (5) and (6) we have got an interpretation of the numbers of those lattice vertices that slide on the hyperboles nearest to the asymptotes. But the analysis of Fig. 10 shows that the numbers of these vertices are Fibonacci numbers. Taking for the sake of simplicity m + n = k and keeping in mind that the successive vertices are situated on the neighboring branches through rotation module, one can come to the following correspondence:

F₁ = · Gch 1 = 1, F₂ = · Gsh 2 = 1,

F₃ = · Gch 3 = 2, F₄ = · Gsh 4 = 3,

F₅ = · Gch 5 = 5, F₆ = · Gsh 6 = 8,

F₇ = · Gch 7 = 13, F₈ = · Gsh 8 = 21,

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

F_k = · Gch k, F_{k + 1} = · Gsh (k + 1). (7)

In the lattice system different recurrent number sequences are realized on different hyperboles. Introducing the hyperbole scale ratio (g) one gets the generalized variant of formulae (7):

u_k = g · · Gch k, u_{k + 1} = g · · Gsh (k + 1). (8)

There is another way of representation of the general member u_k of recurrent sequence:

u_k = A · F_k + B · F_{k + 1}. (9)

Here A and B are the so called initial sequence elements; if recurrent sequence is viewed as an infinite sequence, for instance, …, 12, -7, 5, -2, 3, 1, 4, 5, 9, 14, … , then initial will be two first numbers of sequence part of fixed signs. In this case A = 3, B = 1. In Fibonacci sequence it will be A = 1, B = 0.

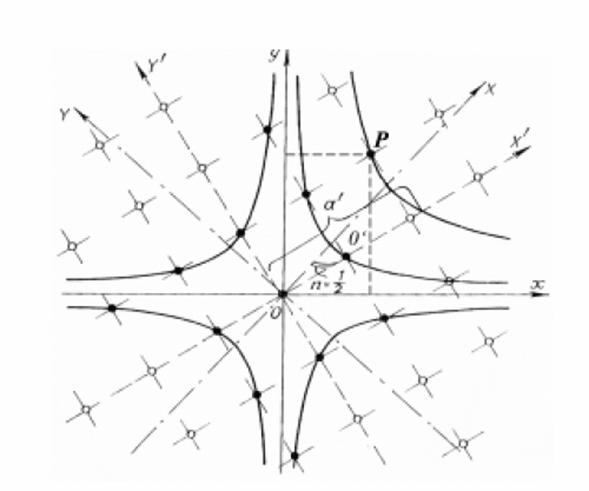
There is another way of obtaining trigonometric interpretation of Fibonacci numbers. There is one interesting arrangement of coordinate axes - X'0X' that is given by the directions of square lattice (Fig. 17).

Fig.17. Analysis of lattice in the system of coordinates X'OY'.

Here hyperbolic angle X0X' is equal to half of the module. If the unit of measurement is the side of cell square, then the coordinates of X' and Y' lattice knots will be integers. It is evident. For the arbitrary vertex P we have:

X'_P = a' · · Gch (m - ),

Y'_P = a' · · Gsh (m + ). (10)

Here a' - hyperbole radius (the orbits of point P) that coincides with 0X' axis. If the counting of angle is done with respect to 0X' axis, then formulae will look like (10):

X'_P = a' · · Gch (Y - 1),

Y'_P = a' · · Gsh Y, (11)

where Y = m + .

This will result in formulae (7) and (8) that correspond to the special case, in particular, when the vertices belonging to the hyperbole that is the nearest to the asymptotes, for which a' = 1. In other words, the vertices coordinates belonging to the single-scale hyperbole are expressed in Fibonacci numbers.

Between the integral-valued coordinates X' and Y' there is a dependence

X'² + X' · Y' - Y'² = a'². (12)

In fact, it expresses the hyperbole equation in reference to the coordinates X'0Y'. At the same time, as the variables X' and Y' successively take on the values of the adjacent numbers of a certain recurrent series, the equation (12) illustrates an important feature of recurrent series, which, taking into account the specificity of formulae (10) and (11), is recorded in the following way:

|u_k² + u_k · u_{k + 1} - u²_{k + 1}| = const. (13)

It is obvious that every series has its own corresponding constant.

Thus, we have got new mathematical interpretation of numerical properties of phyllotaxis dynamic symmetry. As we see, symmetry indicators in phyllotaxis are the integral-valued expressions of golden hyperbolic functions and dynamics of these indicators is presupposed by the regularity of integral-valued growth of golden functions. In this case formula (13) expresses the numerical constant of dynamic symmetry. In particular, for F-phyllotaxis this constant will be 1:

|F_k² + F_k · F_{k + 1} - F²_{k + 1}| = 1.

The phenomenon of divergence also undergoes mathematical interpretation. At the beginning we claimed that divergence angle value in case of F-phyllotaxis numerically coincides with pattern symmetry order, i.e. the divergence angle is changed together with the change of symmetry. Let us consider Fig. 18. We shall analyze the deformation character of the elementary parallelogram 011'0' of the flat lattice. Here there are two important peculiarities. Firstly, in the process of transformation the parallelogram square is preserved: 0P · 00' = const; secondly, the deformation bring about the parallel shift of the bases 00' and 11'.

On the cylinder surface the elementary parallelogram is transformed into the so called elementary belt, therefore it is clear that in the process of transformation such elementary belt will concentrically increase and decrease as to its height (the square will be left unchanged) and simultaneously there will be relative angular displacement of its bases that corresponds to the parallel shift on the involute. 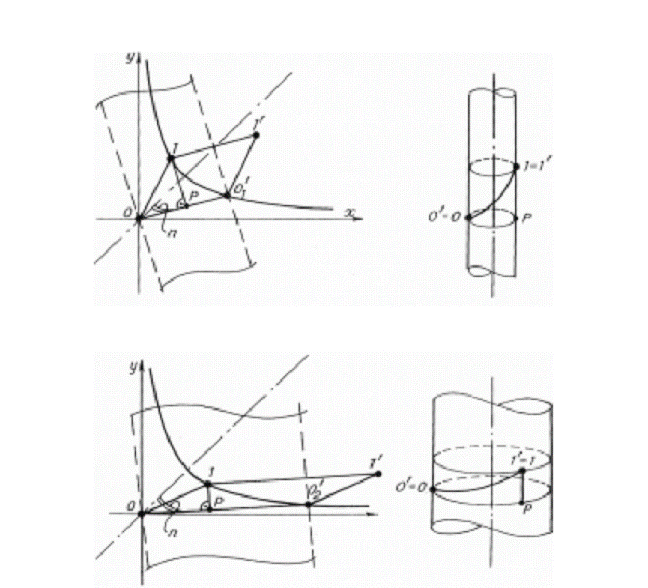Such angular displacement will take place in every elementary belt and this will stipulate the torsion effect on the cylinder surface in general.

The formula of divergence angle comes from the ratio which is equal to:

= = .

The transformations result in:

D = . (14)

Also

= = - F ^{- 1}. (15)

As we see, the angle limit corresponds to the known value of the so called ,,ideal angle" of F-phyllotaxis. It is worth noting that in various ,,non-Fibonacci" сases the divergence angle limit has various values but in all the cases it changes according to the hyperbolic tangent law.

Fig.18. Analysis of hyperbolic transformation of cylindrical surface.

In the analysis process we have also understood the transformation character of the cylinder surface in the process of symmetrical transformation of the cylinder lattice. It is possible to state that this transformation results in three interrelated motions: concentric widening of cylinder along its axis, compression along the axis and torsion.

We shall specify the geometric regularity of cylinder transverse circumference transformation. The radius r of the circumference 00' is increased according to the hyperbolic cosine law:

r == OO' = .

It is obvious that any point of the circumference can be simultaneously presented as the end of the hyperbole movable radius as well as the end of the circumference movable radius. This peculiarity finds its analytical expression in the following:

X' = X (Gch n · cos a ± Gsh n · sin a) + Y (Gsh n · cos a + Gch n · sin a),

Y' = X ( - Gsh n · sin a + Gsh n · cos a) + Y (Gch n · cos a Gsh n · sin a). (16)

Fig.19. Analysis of transformation of cylinder transverse circumference.

With n = 0 we have the formulae for coordinates' transformation that results from the circular rotation:

X' = X · cos a + Y · sin a,

Y' = - X · sin a + Y · cos a.

With a = 0 we have the formulae for coordinates' transformation that results from the hyperbolic rotation:

X' = X · Gch n + Y ·Gsh n,

Y' = X · Gsh n + Y · Gch n.

These formulae reflect the complex motion of the point that is simultaneously a circular and hyperbolic motion. The trajectory of such a motion is a self-intersecting spiral which can be called a composite one (Fig. 20), because it actually illustrates the composition of two rotations.

Fig.20. Composite spiral for which = p.

Thus, the very composite spiral is an expression of geometrical law of cylinder transverse circumference transformation. It finds its laconic representation in a formula:

= const, (17)

which shows the main peculiarity of composite transformation, namely, consistency of angle speeds of hyperbolic rotation (w _h = ) and circular rotation (w = ).

Thus, we have presented the main findings of the phyllotaxis research that contain mathematical explanation of the dynamic symmetry of this phenomenon and allow to generalize on different variants of interpretation of the dynamic symmetry phenomenon, particularly, in architecture.

However, aiming to fully present the mathematics of phyllotaxis we shall briefly mention some other elements of this research. It is necessary to stress that the research was about cylindrical phyllotaxis. But this is only a preliminary stage of theoretical idealization of phyllotaxis. Cone is considered to be more adequate generalization of phyllotaxis pattern. Cylinder as well as disk is considered to be the special case of cone determined by the extreme values - 0 and - of angle of tilt of cone generator to its axis.

We shall remind the essence of the existing ideas about geometrical features of phyllotaxis cone lattices and dynamic mechanism of their pattern formation. It is generally considered that the structure of phyllotaxis cone lattices (arrangement of the vertices) is subject to the law of logarithmic spiral [2, 5, 6]. Thus, to the logarithmic spiral also belong parastichy that form lattices on cone and disk-like patterns and the so called basic (or genetic) spiral that successively runs through all the lattice vertices. Such lattices will be called logarithmic.

Structural and semantic character of the lattice is determined by the two indicators q_л - ratio of local similitude that can be found from the ratio q_л = , where r _k and r _{k + 1} - the distance of two successive primordia to the cone vertex and D - divergence angle. Here there is dependence:

q_л = q ^D, (18)

where q - ratio of the basic spiral similitude.

Fig.21. Analysis of the general case of logarithmic lattice.

Correspondingly, the algorithm of logarithmic lattices pattern formation goes to indicating the primordia motion trajectory, i. e. basic logarithmic spiral and the so called primordial growth interval Dt, or to the intensity of their reproduction N (it is meant that N = ). It is supposed that in nature such a process is stipulated due to equal, in terms of time, primordium growth and thus, the determination conditions for lattice-forming process are as follows: firstly, invariability of local similitude ratio (q_л = = const) and secondly, constant speed of primordium circular rotation w _з:

w _з = = const.

So, this is the classical model of phyllotaxis pattern formation.

The findings of cylindrical phyllotaxis research result in a principally different idea of cone lattices modelling. The idea is that the fundamental regularity of the structural organization of cone phyllotaxis is composite (and not logarythmic) spiral. Parastichy in reality are composite spirals. The same is genetic spiral. Cone transverse circumference transformation also occurs according to the law of composite spiral.

Lattices formed according to the composite spiral law are called natural lattices (Fig. 22).

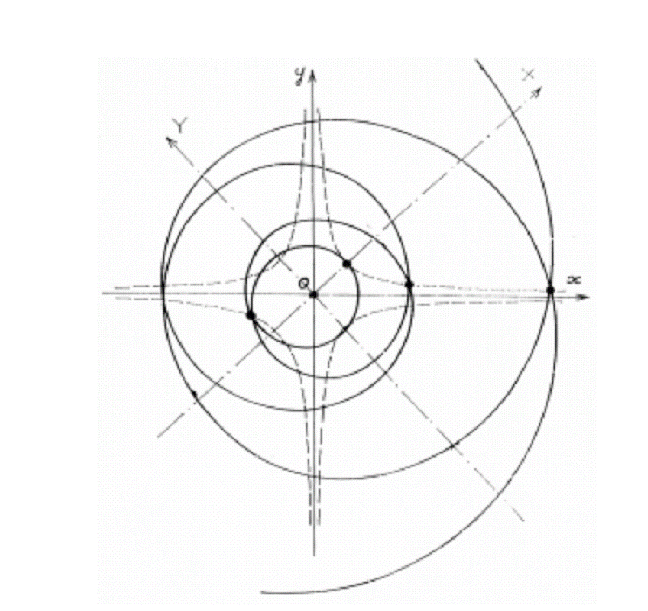
Fig.22. Example of natural lattice with 8:13 symmetry.

They resemble logarithmic ones but, in fact, they are incompatible with them. The reasons and character of this incompatibility can be explained on the comparative drawing of logarithmic and composite spiral (Fig. 23).

Fig.23. Comparative drawing of logarithmic and composite spiral.

As we see, the logarithmic spiral is a peculiar asymptote for the composite one. Different features of logarithmic and natural lattices are explained by different mathematical nature of these two curves. The natural lattice is characterized by the initial scale, which is defined according to the smallest radius of genetic spiral. Evidently, the notion of initial scale does not have any value in reference to the logarithmic lattice.

Of principal importance for the natural lattices is the fact that indicators q_л and D in their structure are not observed in the ideal situations. They only come close to the nominal values as they withdraw from the centre. In the zone of centre of divergence from logarithmic regularity they are evident. In fact, this is violation of similitude. We can specify the divergence regularity. 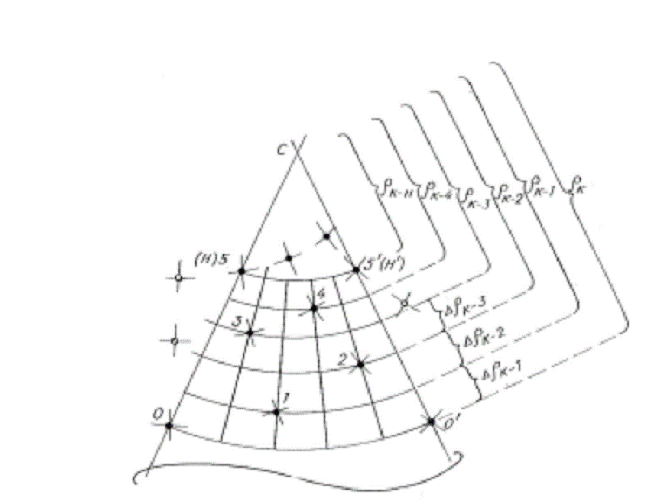For instance, for q_л this regularity is determined by the change of ratio = , where D - the difference of angular hyperbolic coordinates of two successive vertices that belong to the base of belt surface.

Before considering a specific example let us once again stress that the process of lattice pattern formation is determined by the formula = const. The process parameters are the speedsw, w _h and primordium's growth interval Dt or the indicator of their reproduction intensiveness N = . In every specific case the values ofw, w _h and Dt are constant; from them, consequently, one gets nominal characteristics q_л and Da = D that determine the symmetry of the lattice restored. So, Da = w · Dt and q_л = F ^Dn where Dn = w _h · Dt is the angular hyperbolic interval between the successive primordia.

Now let us consider Fig. 24. It shows ,,top view" and ,,side view" of the natural cone lattice with 1 : 1 symmetry. In this case Da = p , Dn = 1. Let us find the ratio limit :

q_л = = = F.

Here are specific data for several initial points:

k	1	2	3	4	5
n
	1,0	1,414 …	1,581 …	1,612 …	1,618 ..

Fig.24. Scheme that explains the origin of the Golden section in the off-shoots structures.

We have specially chosen the simplest example which one often observes in nature - on trees and plants off-shoots. It also explains mathematical reasons for the origin of golden proportion in the linear correlations of off-shoots structures, in particular, the fact that proportion discovered in off-shoot natural measurements in fact approximates golden section. Here golden section cannot be realized in its absolute value.

And some more words about natural lattices symmetry transformation. We shall not describe it in details but emphasize that this transformation is based on composite motion - composite rotation that combines both hyperbolic and circular rotation. This issue will be discussed in a separate article.

Finally, we shall do the generalizations. Besides Hambidge's variant we shall use in our comparative research another theoretical result which is well-known in architecture - Modular of French architect of Le Corbusier.

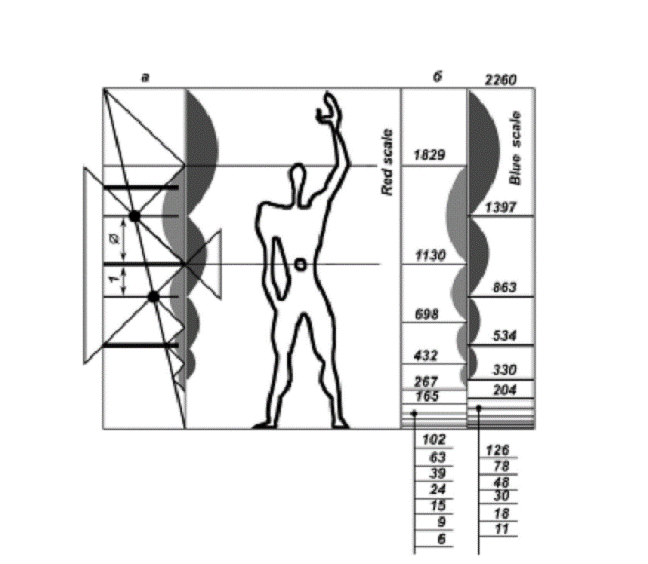
Fig.25. a - scheme of continuous section division in the golden proportion.

B - integral-valued scales that were obtained as a result of approximation of irrational scales values.

Fig. 25 on the left shows the scheme suggested by the author of Modular to illustrate the infinite division of section in the golden proportion. Le Corbusier links such a division to the proportions of human figure. On the right side of the drawing one can see the so called red and blue scales where irrational numerical values obtained by means of infinite division scheme are represented in approximated integral-valued way. It is clear that irrational numbers express the golden exponential function. Integral-valued sequences onto which Le Corbusier transfers the additive features of the golden sequence can be considered recurrent to a certain degree of conventionality. Le Corbusier presents the formulae of red and blue scales in the following way:

a _n = k ∙ F ⁿ, b _n = 2k ∙ F ⁿ,

where n is an arbitrary integer; k - dimension factor equal 1,13 m.

He also accepts that:

a _{n - 2} + a _{n - 1} = a _n,

b _{n - 2} + b _{n - 1} = b _n.

Naturally, due to approximation on certain section of integral-valued sequences additivity is violated: the golden sequence and its integral-valued approximations ideally cannot coincide as they express various mathematical regularities.

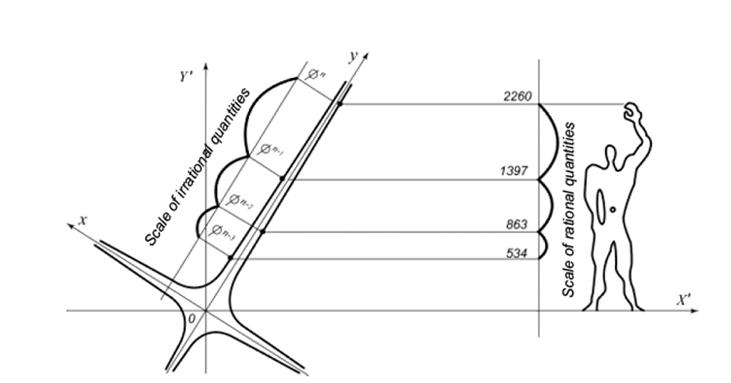
But we have to show how to adjust the imbalance. Modular irrational and integral-valued scales are to be in some ways linked to the hyperbolic coordinates axes (Fig. 26). The sequence of irrational relations will be reflected on the axis 0y, the integral-valued sequences will be created from Y' coordinates by the same series of points located on the neighboring hyperbole branches through one rotation module.

Fig.26. Reference of Modular scales to axes of hyperbolic coordinates.

So, what are the common features of phyllotaxis dynamic symmetry, Modular and Hambidge's dynamic symmetry? The answer is that in all these cases we deal with the same mathematical regularities, namely, golden hyperbolic functions. Really, on Hambidge's scheme (Fig. 2) the base of the arbitrary parallelogram can be interpreted through the golden sine (Gsh x) and diagonal- through the golden cosine (Gch x). Then we get the formula of J. Hambidge's invariant of dynamic symmetry:

Gch² x - Gsh² x = 1.

Of similar interest is the possibility of Modular numerical regularities interpretation. The numerical sequences of red and blue scales are considered recurrent (ignoring some ,,small" ambiguities); it means, we can apply to them the formula of constant (invariable) of phyllotaxis dynamic symmetry:

|u_n² + u_n · u_{n - 1} - u² _{n - 1}| = const.

Let us determine the invariant value for the red scale. We take any couple of neighboring numbers, for example, 6 and 9. We shall get |6² + 6 · 9 - 9²| = 9. Now we shall determine the invariant for the blue scale. We take numbers 18 and 30: |18² + 18 · 30 - 30²| = 6. It is necessary to remember that the formula used in this case reveals characteristic dependence (12) of golden hyperbolic trigonometry, discovered by us.

The numbers of red and blue scales can be considered as hyperbolic coordinates X' and Y' of square lattice vertices (see Fig. 17) that belong to two specific hyperboles. For one of them a' = const = 9, for the other - a' = const = 6.

Our generalization will be incomplete if we do not remind that features of space-time in special theory of relativity is also characterized by invariant. Such invariant is the so called special-temporal interval which value is preserved in the process of transfer from one inertial system to the other and is expressed in the formula Dt² - Dx² = const. Here dependence of hyperbolic trigonometry ch² x - sh² x = const also is the mathematical sub base of this expression

Thus, we have grounds for the final conclusions.

1. Mathematical research of phyllotaxis described above establishes the fact that this phenomenon shows regularities of non-Euclid, to be more specific, pseudo-Euclid geometry more known as Minkowski's geometry. So far, physics was considered to be the only field where this geometry was realized. But it was V. E. Vernadskiy who suggested that the laws of natural pattern formation are based on non-Euclid geometry. [6]. Therefore, our findings can be considered as those that specify of V. E. Vernadskiy's suggestions.

2. Phyllotaxis geometry and its trigonometric apparatus reflect peculiarities of mathematics of nature. This is the form of mathematics where fundamental role belongs to golden section.

3. J. Hambidge's principle of dynamic symmetry, Le Corbusier's proportional system of Modular, phyllotaxis dynamic symmetry as well as spatial-temporal invariant of special theory of relativity have common mathematical grounds of Minkowski's geometry regularities. Therefore, there are substantial grounds to refer to them as common regularities of art and nature.